一、背景
我们从最最最简单的场景开始,假设在一个二维平面上,现有N个点,如下图所示

现在给你一个点,求K个最近的点(欧式距离),如下图所示
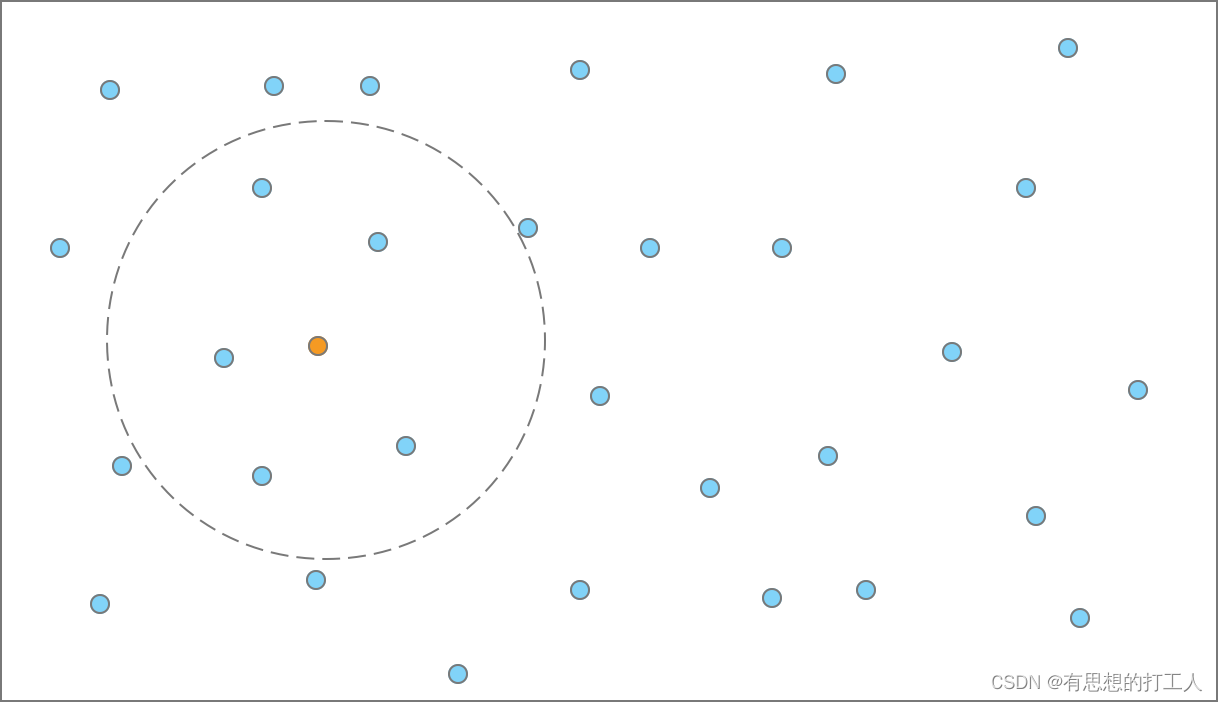
肉眼很容易可以看出,以query点为中心画个圆,慢慢往外扩展,直到包含K个点,然后这K个点就是最近的点。
看起来很容易,但这得给算法实现个眼睛啊!
二、暴力解法
这里需要遍历所有的N个点跟query点分别求个距离,然后找出K个最相近的点。
咱们专注于这个算法本身,假设距离计算的复杂度为1,那么暴力解法的复杂度为:N + NlogK
假设N很大,在没有考虑距离计算的复杂度前提下,其实这复杂度已经很高了。那如果是单机,估计实现不了在线实时计算了,有没有办法解决呢?
三、分布式解法
把点随机分布到不同机器上,然后求解的时候每台机器都算个top K出来,再合并。如下图所示:
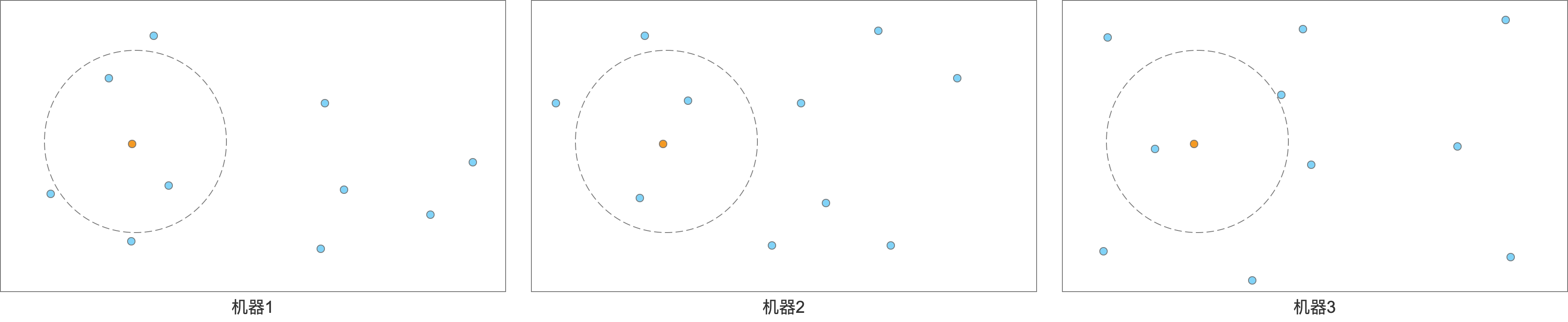
其实这样整体复杂度并没有变化,只是利用机器资源换取时间,理论上只要机器够多,耗时还是能降低很多的。
如果没有很多机器资源,可以考虑下更优的解法。
四、分布式解法优化——IVF
既然都已经把N个点划分成A(3)个区域了,划分方法能否考虑下距离?比如最简单的按距离划分,如图所示:
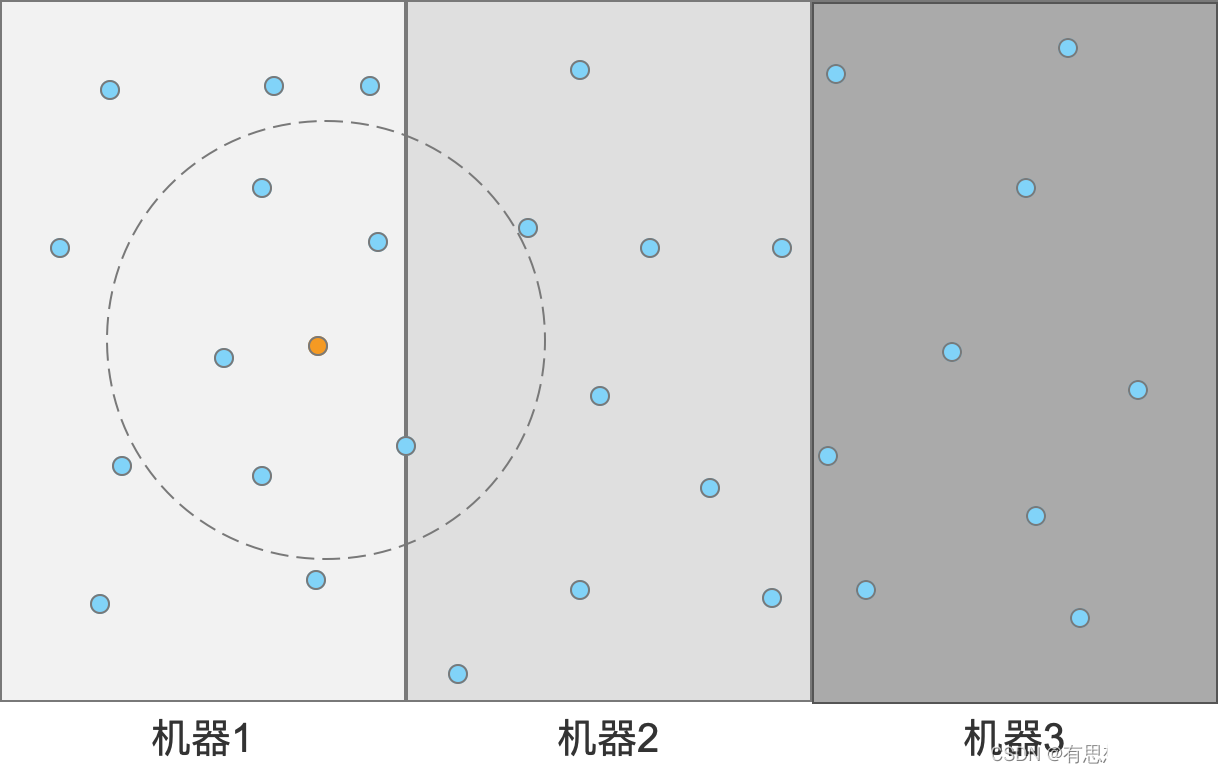
这时我们在检索的时候,只需要在最近的B(>A=3)个区域暴力检索就行了。
如果A=3,B=1,那么复杂度就是: (N+NlogK)/3,这个复杂度是有很大的降低的,但是会有一个缺点,精度有所降低。如果上图所示,划分后的结果,会导致一个点出错~
实际构建区域步骤
- 对所有点集合抽样一份小的集合。
- 利用聚类算法(一般是Kmean)得出A个聚类中心点。
- 把所有点都按距离分配到每个聚类中心,得到A个点集合。
实际检索步骤
- 在A个聚类中心点中,暴力找出B个最近的聚类中心点
- 只在B个聚类中心点所属点集中,暴力检索最近的top K个点
实际复杂度
(N + NlogK)B/A + A
A为聚类中心个数,B为检索查询的聚类中心数
虽然这种方法已经大大降低了复杂度,但还有更有的方式吗?
五、图论算法——NSW
其实就是把N个点按一定规则连边,构成一个有向图,如下图所示:
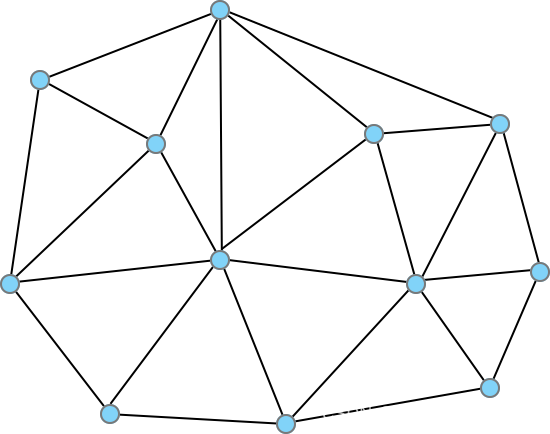
蓝色点为点集,黑色边为有向边,具体如何构造这个有向边后边再说,先说下检索流程
检索流程
如下图所示:
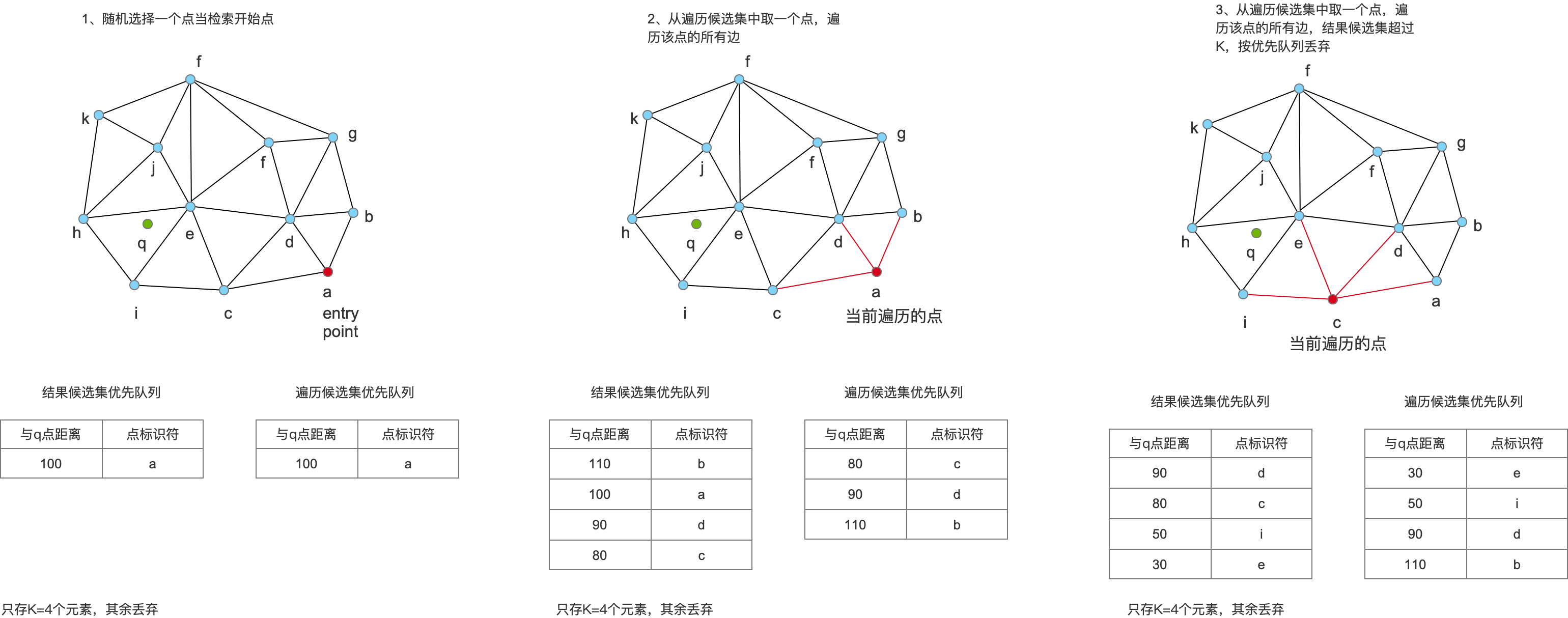
-
给出一个query点,如上图 红色点
-
初始化一个点集访问记录存储
-
初始化两个优先队列,一个存储结果候选集,只存K个元素,一个存储遍历候选集
-
随机找一个点,当作进场开始点(如上图右下角红点,entry point)
-
entry point 加入遍历候选集,如果它并不是标记为删除的,把它放入结果候选集;
-
从遍历候选集中取出距离query点最近的点,遍历与它所有关联的点,检查是否已经访问过
- 如果它已经访问过,直接跳过
- 如果没有访问过加入遍历候选集,如果关联点并不是标记为删除的,把它放入结果候选集。
-
重复第6步骤,直到遍历候选集中距离query最近的点,都比结果候选集距离query最远的点距离query大,并且结果候选集已经足够K个点就结束。
新增构建步骤
- 给出一个待新增的点 A
- 在图中检索出top k个点,k = ef_construction
- 从点A 连接其中M_个点,这M_个点从 top k里面选择,后面简称M_个点里面当前遍历的点为点B
- 遍历每条新增连边,检查是否有相应的反向连边,也就是从点B到点A的连边
- 如果有就跳过
- 如果没有就给反向边连上
- 如果点B的连边没有超过M_, 直接连上就行
- 如果点B的连边超过了M_, 需要重新选择M_个点,保证点B只有外出M_条边
简单的说,其实就是找出top k近邻,然后连边。重点问题在于,如果 K > M_,怎么选择更加合适的邻居呢?
最简单的方式:按距离排序,选择跟新增点最近的那些。这样有可能形成孤岛,导致整个图并不是连通图,有没有更好的方式呢?
优质邻居选择方式
如下图所示:
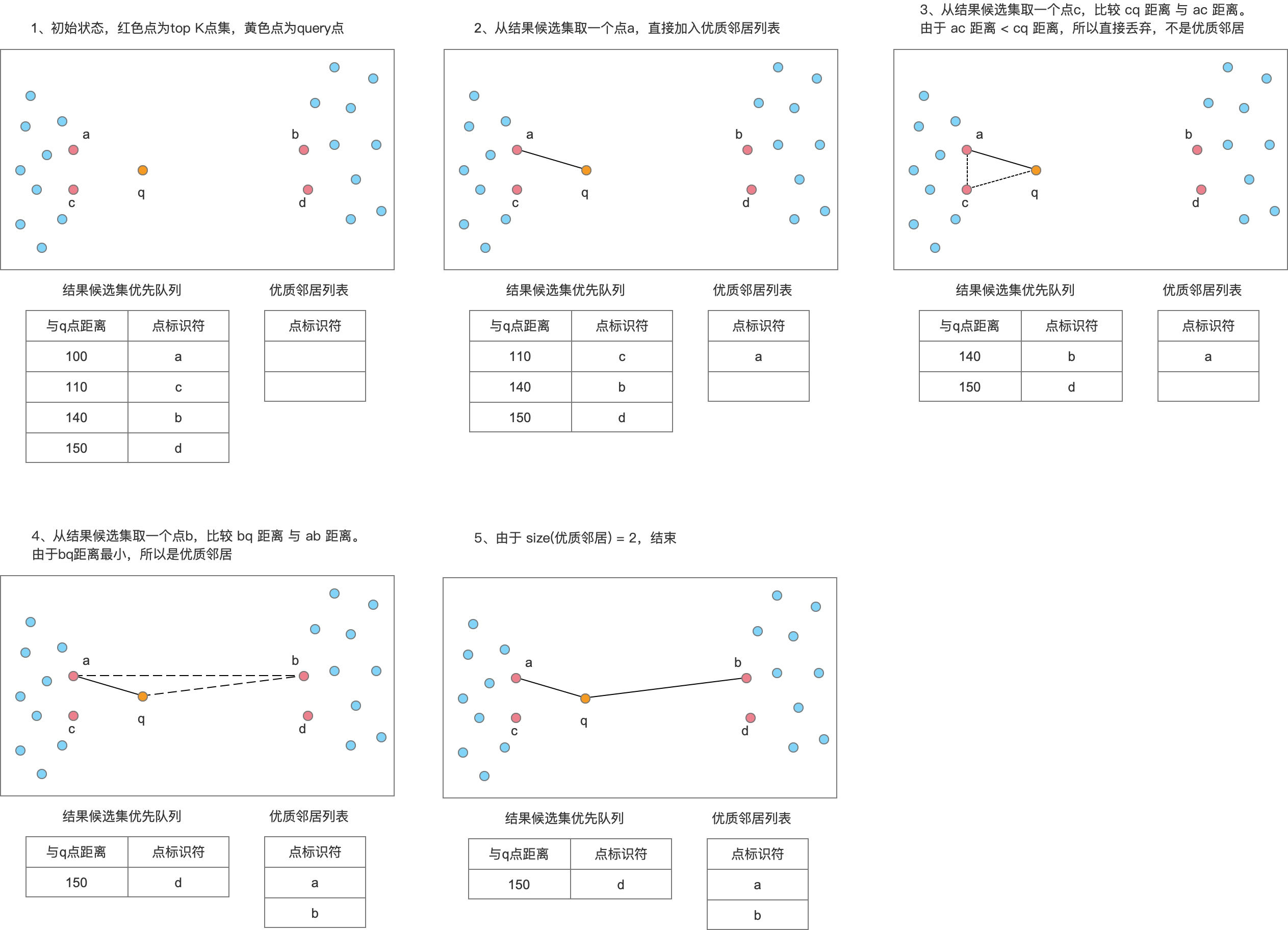
-
给出一个query点(黄色),top K结果候选集(红色)
-
初始化一个结果候选集的优先队列,一个优质邻居列表
-
从结果候选集取出一个点,判断该点与query的距离,是不是比该点与优质邻居的距离都大
- 如果是,加入优质邻居列表
- 如果不是,丢弃
其实就是把连边的点尽量分散。
更新点构建步骤
- 初始化两个set 集合A、B
- 集合A存更新点的所有邻居,集合B存更新点的 所有邻居 & 所有邻居的邻居
- 给集合A里面的所有点,从集合B里面重新选择合适的邻居
- 重新跑一遍新增点的流程,见上面的新增
六、图论算法优化——HNSW
其实它就是 Skip list + NSW,我们先回顾下跳表的结构吧。
跳表
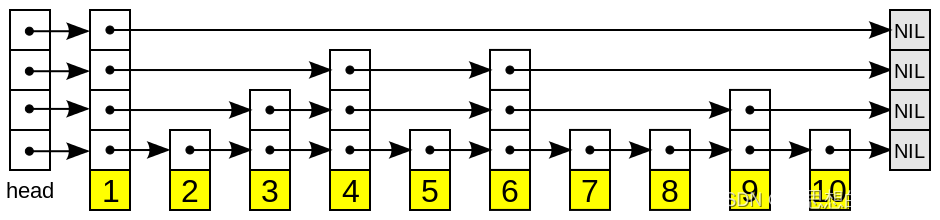
这是一种很常见的数据结构,这里就不详细描述了。
真正的HNSW结构
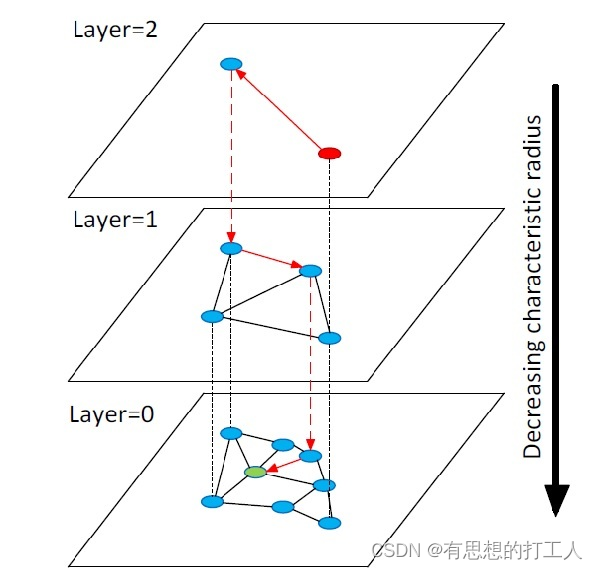
如上图所示,其实HNSW 就是 Skip List + NSW。
跳表也是分层的,但是真正的跳表每一层是一条有序列表。
然而在HNSW中,也是跟跳表一样分层,这里每一层就是一个NSW有向图。
加上跳表思想后,nsw的操作只有一个不同的点。检索进场点是上一层的得到的最近的点,当然最上面一层还是随机点进场。
这种算法复杂度理论上是logN的,当然也只是理论上哈,而且又一定的精度损失~
实际场景
实际场景上
- 如果内存够大能撑住NSW所需的内存,可以考虑直接上HNSW
- 如果内存不够,可以考虑IVF + HNSW 或者 直接随机分布 + HNSW