首页 > 其他分享 >树链剖分

树链剖分

时间：2023-10-06 12:58:22浏览次数：35  
标签：剖分 int top dfs 树链 dfn son 节点

前言：

本人太弱了，看着题解调了一下午，才A了树剖的板子题，所以写篇博客纪念一下（其实是怕自己忘了树剖怎么做）。

本文以板子题为例子

定义:

树链剖分，计算机术语，指一种对树进行划分的算法，它先通过轻重边剖分将树分为多条链，保证每个于且只属于一条链，然后再通过数据结构（树状数组、BST、SPLAY、线段树等）来维护每一条链　　————百度百科

我们把这种高级的定义翻译成人话来讲，就是把一棵树，用一种叫做轻重链剖分的方法，划分成多条链，然后再对每一条链进行操作。

正文

在学习树剖之前，需要先明白一些定义：

  • 重儿子：对于每一个非叶子节点，它的子节点中，子树大小最大的那个子节点被称为重儿子。
  • 轻儿子：对于每一个非叶子节点，除了重儿子以外的子节点都是它的轻儿子。
  • 重边：任意两个重儿子以及重儿子和其父节点之间的连边称为重边。
  • 轻边：除去重边剩下的边。
  • 重链：多条（$\geq $1）重边相连组成的链即为重链，且重链一定以轻儿子为起点。
  • 此外，若一个叶子节点是轻儿子，那么它也可以视为一条重链。

了解了这些以后，再来看一下我们要处理的问题：

  • 将树从 $ x $ 到 $ y $ 结点最短路径上所有节点的值都加上 $ z $。
  • 求树从 $ x $ 到 $ y $ 结点最短路径上所有节点的值之和。
  • 将以 $ x $ 为根节点的子树内所有节点值都加上 $ z $。
  • 求以 $ x $ 为根节点的子树内所有节点值之和。

emmm，区间求和，区间查询，那么显而易见，用线段树来维护！

所以，第一步，我们要先将整棵树剖分成一条条链，需要用到两次 dfs（轻重链剖分）。

dfs，轻重链剖分

第一次 dfs 处理出每个节点的深度，重儿子，父亲，以及每个节点的子树大小。

  void dfs1(int u,int f){//u是当前节点，f是父节点 
      int max_son=-1;//max_son里存的是当前重儿子的子树大小，用来找出重儿子 
      dep[u]=dep[f]+1;
      fa[u]=f;
      sz[u]=1;//sz:子树大小 
      for(int i=head[u];i;i=edge[i].nex){//遍历所有连边 
          if(edge[i].to!=f){//因为树相当于一棵无向图，这句话保证了只会向下接着搜，不会搜到父节点 
              int y=edge[i].to;
              dfs1(y,u);//处理子节点 
              sz[u]+=sz[y];
              if(sz[y]>max_son) 
              {
                  son[u]=y;
                  max_son=sz[y];
              }//找出重儿子 
          }
      }	
  }

接着我们进行第二次 dfs，这次需要处理出每个节点的 dfs 序，并且将初始值赋值到新的 dfn 数组里；记录每条链的顶端。

  void dfs2(int u,int topx){	//topx为当前节点所在重链的链顶 
      dfn[u]=++cnt;			//dfn数组存着的是每个节点的dfs序 
      pos[cnt]=a[u];			//这句话的意思dfs序为cnt的点的值为a[u] 
      top[u]=topx;			//top记录每个点所在重链的链顶 
      if(!son[u]) return ;	//没有儿子则返回 
      dfs2(son[u],topx);		//处理重儿子 
      for(int i=head[u];i;i=edge[i].nex)//处理剩下的轻儿子 
      {
          int y=edge[i].to;
          if(y==fa[u]||y==son[u]) continue;
          dfs2(y,y);
      }
  }

大家可以注意到，我们先处理了重儿子，再处理的轻儿子，为什么呢？

因为我们在第二次 dfs 中，记录了每个点的 dfs 序。先处理重儿子，可以保证每一条重链上的重儿子 dfs 序是连续的，方便我们的查询操作。

线段树略。

修改&查询

  • 将树从 $ x $ 到 $ y $ 结点最短路径上所有节点的值都加上 $ z $。

与求 LCA 相似，每一次我们让链顶深度较深的点向上跳到链顶的父亲，并对这条链进行操作，直至两个点在一条链上。其实这也就是树剖求 LCA 的过程。

  void add_1(int x,int y,int k){
      k%=p;
      while(top[x]!=top[y]){                    //如果不在一条链上 
          if(dep[top[x]]<dep[top[y]]) swap(x,y);//就让所在链 链顶深度较深的那个点向上跳 
          modify(1,dfn[top[x]],dfn[x],k);       //一次跳一整条链，并且修改这条链上的值 
          x=fa[top[x]];                         //这条链跳到顶了，向上跳到上一条链 
      }
      if(dep[x]>dep[y]) swap(x,y);//最后在同一条链上时，两个点之间还有未修改的，修改这些点 
      modify(1,dfn[x],dfn[y],k);
  }//最后说一下modify(线段树区间修改) 因为dfs序在一条链上是连续的，所以这里dfn[top[x]]就相当于
   //左节点，dfn[x]相当于右节点

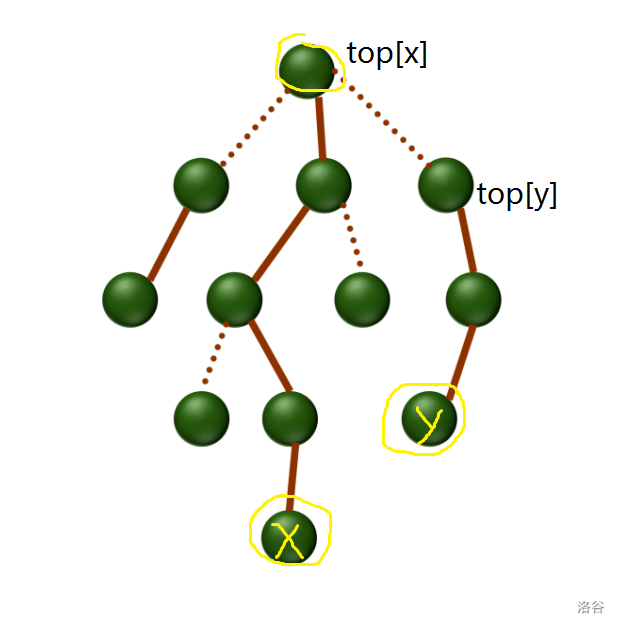
大家可以配合这张图片好好理解。

  • 求树从 $ x $ 到 $ y $ 结点最短路径上所有节点的值之和。

这个操作和操作 \(1\) 差不多，也是在求 LCA 时累加，代码实现也几乎相同

  int query_2(int x,int y){
      int ans=0;
      while(top[x]!=top[y])//同上 
      {
          if(dep[top[x]]<dep[top[y]]) swap(x,y);
          ans+=query(1,dfn[top[x]],dfn[x]);//线段树查询 
          ans%=p;
          x=fa[top[x]];
      }
      if(dep[x]>dep[y]) swap(x,y);
      ans+=query(1,dfn[x],dfn[y]);
      return ans%p;
  }
  • 将以 $ x $ 为根节点的子树内所有节点值都加上 $ z $。
  • 求以 $ x $ 为根节点的子树内所有节点值之和。

在我们链剖的时候，已经将一棵立体的树剖分为一条线段了，而下标就是求出来的 dfs 序。又因为 dfs 序不光在一条链上是连续的，在子树里也是连续的，所以用线段树的区间查询和修改很容易就可以实现

  void add_3(int x,int k){
      k%=p;
      modify(1,dfn[x],dfn[x]+sz[x]-1,k);//不要忘了-1 
  }
  int query_4(int x){
      return query(1,dfn[x],dfn[x]+sz[x]-1);//同上 
  }

完整代码（亿点点长）

  #include<iostream>
  #include<cstdio>
  #include<algorithm>
  #include<cmath>
  #include<cstring>
  #include<string>
  #define in inline
  #define re register
  #define FOR(i,a,b) for(re int i=a;i<=b;i++)//奇怪的码风qwq 
  #define ROF(i,a,b) for(re int i=a;i>=b;i--)
  #define pushup(u) tree[u]=tree[u<<1]+tree[u<<1|1]
  using namespace std;
  int const N=2e5+5;
  //------------
  in int read()
  {
      int x=0,f=1;char ch=getchar();
      while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();}
      while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
      return f*x;
  }
  //------------
  int n,m,r,p;
  int cnt=0;
  int a[N],pos[N];
  int dep[N],sz[N],fa[N],son[N],top[N],dfn[N];
  //-----------------------------------线段树 
  struct node{
      int l,r,sum,len,lazy;
      node operator +(const node &x)const{
          return (node){l,x.r,(sum+x.sum)%p,len+x.len,0};
      }
  }tree[N<<2];
  void build(int u,int l,int r){
      if(l==r)
      {
          tree[u]=(node){l,l,pos[l]%p,1,0};//线段树是来维护每条链的，顺序是求出的dfs序，所以这里不是原先的a数组，而是pos数组
          return ;                      
      }
      int mid=l+r>>1;
      build(u<<1,l,mid);
      build(u<<1|1,mid+1,r);
      pushup(u);
  }
  void pushdown(int u){
      int l=u<<1,r=u<<1|1;
      tree[l].lazy+=tree[u].lazy;
      tree[r].lazy+=tree[u].lazy;
      tree[l].sum+=tree[u].lazy*tree[l].len;
      tree[r].sum+=tree[u].lazy*tree[r].len;
      tree[l].sum%=p;
      tree[r].sum%=p;
      tree[u].lazy=0;
  }
  void modify(int u,int l,int r,int k){
      node y=tree[u];
      if(y.l>=l&&y.r<=r)
      {
          tree[u].lazy+=k;
          tree[u].sum+=k*tree[u].len;
          tree[u].sum%=p;
          return ;
      }
      if(tree[u].lazy) pushdown(u);
      if(y.l>r||y.r<l) return;
      else
      {
          modify(u<<1,l,r,k);
          modify(u<<1|1,l,r,k);	
      } 
      pushup(u);
  }
  int query(int u,int l,int r){
      node y=tree[u];
      if(y.l>=l&&y.r<=r)
          return tree[u].sum%p;
      pushdown(u);
      if(y.l>r||y.r<l) return 0;
      return query(u<<1,l,r)+query(u<<1|1,l,r);
  }
  //-------------------------------链剖
  void add_1(int x,int y,int k){
      k%=p;
      while(top[x]!=top[y]){                    //如果不在一条链上 
          if(dep[top[x]]<dep[top[y]]) swap(x,y);//就让所在链 链顶深度较深的那个点向上跳 
          modify(1,dfn[top[x]],dfn[x],k);       //一次跳一整条链，并且修改这条链上的值 
          x=fa[top[x]];                         //这条链跳到顶了，向上跳到上一条链 
      }
      if(dep[x]>dep[y]) swap(x,y);//最后在同一条链上时，两个点之间还有未修改的，修改这些点 
      modify(1,dfn[x],dfn[y],k);
  }//最后说一下modify(线段树区间修改) 因为dfs序在一条链上是连续的，所以这里dfn[top[x]]就相当于
   //左节点，dfn[x]相当于右节点 
  int query_2(int x,int y){
      int ans=0;
      while(top[x]!=top[y])//同上 
      {
          if(dep[top[x]]<dep[top[y]]) swap(x,y);
          ans+=query(1,dfn[top[x]],dfn[x]);//线段树查询 
          ans%=p;
          x=fa[top[x]];
      }
      if(dep[x]>dep[y]) swap(x,y);
      ans+=query(1,dfn[x],dfn[y]);
      return ans%p;
  }
  void add_3(int x,int k){
      k%=p;
      modify(1,dfn[x],dfn[x]+sz[x]-1,k);//不要忘了-1 
  }
  int query_4(int x){
      return query(1,dfn[x],dfn[x]+sz[x]-1);//同上 
  }
  //----------------------------链式前向星 
  struct E{
      int to,nex;	
  }edge[N<<1];
  int head[N],tot;
  void add(int u,int v){
      edge[++tot].to=v;
      edge[tot].nex=head[u];
      head[u]=tot;
  }
  //------------------------2*dfs
  void dfs1(int u,int f){//u是当前节点，f是父节点 
      int max_son=-1;//max_son里存的是当前重儿子的子树大小，用来找出重儿子 
      dep[u]=dep[f]+1;
      fa[u]=f;
      sz[u]=1;//sz:子树大小 
      for(int i=head[u];i;i=edge[i].nex){//遍历所有连边 
          if(edge[i].to!=f){//因为树相当于一棵无向图，这句话保证了只会向下接着搜，不会搜到父节点 
              int y=edge[i].to;
              dfs1(y,u);//处理子节点 
              sz[u]+=sz[y];
              if(sz[y]>max_son) 
              {
                  son[u]=y;
                  max_son=sz[y];
              }//找出重儿子 
          }
      }	
  }
  void dfs2(int u,int topx){	//topx为当前节点所在重链的链顶 
      dfn[u]=++cnt;			//dfn数组存着的是每个节点的dfs序 
      pos[cnt]=a[u];			//这句话的意思dfs序为cnt的点的值为a[u] 
      top[u]=topx;			//top记录每个点所在重链的链顶 
      if(!son[u]) return ;	//没有儿子则返回 
      dfs2(son[u],topx);		//处理重儿子 
      for(int i=head[u];i;i=edge[i].nex)//处理剩下的轻儿子 
      {
          int y=edge[i].to;
          if(y==fa[u]||y==son[u]) continue;
          dfs2(y,y);
      }
  }
  //---------------------------------------------主程序 
  int main()
  {
      n=read(),m=read(),r=read(),p=read();
      FOR(i,1,n) a[i]=read();
      FOR(i,1,n-1)
      {
          int u,v;
          u=read(),v=read();
          add(u,v),add(v,u);
      }
      dfs1(r,0);
      dfs2(r,r);
      build(1,1,n);
      int opt,x,y,z;
      FOR(i,1,m)
      {
          opt=read(),x=read();
          if(opt==1)
          {
              y=read(),z=read();
              add_1(x,y,z);
          }
          else if(opt==2)
          {
              y=read();
              printf("%d\n",query_2(x,y)%p);//注意取膜，不然容易炸，会RE 
          }
          else if(opt==3)
          {
              z=read();
              add_3(x,z);
          }
          else
          {
              printf("%d\n",query_4(x)%p);//同上 
          }
      }
      return 0;
  }

完结撒花qwq

  • 2022.11.5 update:
    经djh老师指正，\(max\)_\(son\) 不能定义成全局变量。

  • 2023.8.8 update:
    删改了无用语句，优化了排版。

标签：剖分,int,top,dfs,树链,dfn,son,节点
From： https://www.cnblogs.com/LHLeisus/p/-shab.html

相关文章

  • [学习笔记] 树链剖分
    叫复习笔记或许更好。树链剖分就是把树剖成链去解决一些问题。定义重子节点：子节点中子树大小最大的节点。轻子节点：除重子节点外的其他子节点。重边：到重子节点的边。轻边：到轻子节点的边。记号\(dfn[x]\)：DFS序，也是在线段树中的编号。\(son[x]\)：重子节点。\(dep[x]\)......
  • 「学习笔记」树链剖分
    树链剖分用于将树分割成若干条链的形式，以维护树上路径的信息。具体来说，将整棵树剖分为若干条链，使它组合成线性结构，然后用其他的数据结构维护信息。树链剖分有很多种形式，本文要讲的是其中的轻重链剖分。树链剖分本质上就是把链从树上砍下来，然后放到树状数组或线段树上来维护。......
  • 长链剖分
    例题：P5903【模板】树上k级祖先题目描述思路长链剖分模板题。长链剖分：计算\(f[i][j]\)表示\(i\)的\(2^j\)级祖先；计算\(up[i][j]\)表示\(i\)的\(j\)级祖先；计算\(down[i][j]\)表示在长链上从\(i\)向下走\(j\)步到达的祖先。计算\(i\)的\(k\)级祖......
  • 树链剖分学习(复习?)笔记
    树链剖分，即树剖。顾名思义，树链剖分就是将一棵树通过某种方式剖分成若干条链，再利用\(dfs\)序，从而将树上的问题转化为序列上的问题。树剖的方式有不止一种，比如重链剖分、长链剖分。最常用的(大概?)是重链剖分。此处介绍重链剖分。首先，我们定义一个节点的重儿子为此节点的所有儿......
  • 树链剖分/重链剖分模板
    #include<bits/stdc++.h>usingnamespacestd;intn,m,d,mod,w[200005],wt[200005],e[200005],ne[200005],h[200005],idx=1,t[800005],l[800005],r[800005],tag[800005];intson[200005],id[200005],fa[200005],cnt,dep[200005],siz[200005],top[200005];/*son[]重儿子......
  • 『复习笔记』树链剖分（重链剖分）
    前言（事出必有因）今天模拟赛有一道线段树+LCA的题，考场上码了两个小时，结果pushup错了，结果线段树调完了，发现TLE了，原来是求LCA炸了。。因为我用的倍增（我就是倍增狗你能把我怎么样），但是倍增的一个重要问题就是log都跑满了，但是树剖跑不满log，别问我为什么不用Tarjan，因为这题是在线的不好......
  • 树链剖分 | 洛谷 P4114 Qtree1
    前言题目链接：洛谷P4114Qtree1前置知识：树链剖分题意给定一棵树，有修改边权和查询两点之间边权最大值两种操作，对于每个查询输出结果。解析已经在前置博客里提到，树链剖分可以将树上的任意一条路径划分成不超过\(O(\logn)\)条连续的链，保证划分出的每条链上的节点DFS序......
  • 树链剖分详解
    目录前言一、树剖是什么？二、重链剖分树剖的实现例题总结前言在同学们一路走来的过程中，一定已经学习了倍增求LCA的算法。倍增求LCA算法只适用于少部分情况，那么，如果要求在求出LCA的同时，对两点\(a,b\)之间的所有点权（或边权）进行求和或修改，又该怎么做呢？这里介绍一种树链......
  • 杭电23多校第九场Capoo on tree（二分+树链剖分+可持久化线段树）
    2023HDU多校9__Capooontree（二分+树链剖分+可持久化线段树）题目链接Solution\(Hint1\)考虑如何进行对某一相同点权的所有点进行点权\(+1\)操作，如果我们建立权值线段树，那只需要将权值为\(x\)的点并入权值\(x+1\)即可，但是这样就算我们建立以节点编号为版本的可持久化线段树，也是......
  • VTK 实例58：三角剖分（表面重建）
    1#include<vtkAutoInit.h>2VTK_MODULE_INIT(vtkRenderingOpenGL2);3VTK_MODULE_INIT(vtkRenderingFreeType);4VTK_MODULE_INIT(vtkInteractionStyle);56#include<vtkSmartPointer.h>7#include<vtkProperty.h>8#include<vtkPo......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99