note ODT

（珂朵莉图压压惊）

适用场景：不断区间修改、区间询问，数据随机

ODT：old driver tree（老司机树），又名珂朵莉树，是一个骗分的好东西。其内部是基于 std::set 实现的，而 std::set 是基于红黑树实现的，所以我觉得应该是算法，但是对于ODT究竟是算法还是数据结构有争议。

在随机数据下跑得飞快，吊打线段树啥的，时间复杂度为\(O(NloglogN)\)
但是在毒瘤数据下会被卡掉qwq。所以一般用来骗分

其他啥的不讲了，网上一大堆，上正题。

ODT 的主要思想是随机数据很可能使得一大段连续数字相同，因此我们可以把这一整段当成同一个数来处理。

举个栗子（借大佬图一用）：

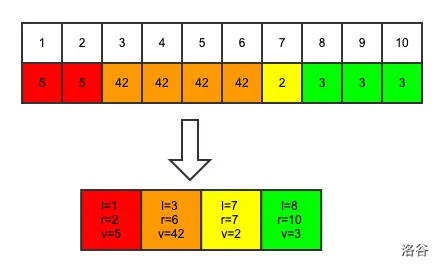
原来需要处理 \(10\) 个数，现在处理 \(4\) 个数即可。（这也是为什么会被卡掉qwq）

讲讲代码实现

为了偷懒方便快捷，可读性增强，我们一般会

#define iit set::iterator

注：iit可改成自己喜欢的，作者不想按shift，故使用iit

初始化，重载运算符。没啥好讲的

struct odt{
	int l,r;
	mutable int v;
	odt(int L=0,int R=-1,int V=0):l(L),r(R),v(V){}
	friend bool operator<(odt a,odt b){
		return a.l<b.l;
	} 
};

敲黑板划重点 ODT重要操作 区间分裂（split）

我们操作的区间并不总是正好覆盖我们存储的区间。因此我们需要一个函数来实现分裂开每个区间的操作，也就是split函数。

split函数接受一个参数 \(pos\)，然后把包含 \(pos\) 的区间 \([l,r]\) 分裂成 \([l,pos)\) 和 \([pos,r]\)

iit split(int pos){
	iit it=s.lower_bound(pos);
	if(it!=s.end()&&it->l==pos)
		return it;
	--it;
	if(pos>it->r)
		return s.end();
	int l=it->l,r=it->r,v=it->v;
	s.erase(it);
	s.insert(odt(l,pos-1,v));
	return s.insert(odt(pos,r,v)).first;
}

敲黑板划重点 ODT重要操作 区间推平/区间赋值（assign）

如果操作中全是split的话，区间越来越多，那么必然会T飞（再多看一眼就快爆炸），所以这时我们就需要区间赋值操作减少区间数量assign。

assign函数要传 \(3\) 个参，分别表示区间左端点（ \(l\) ) 、区间右端点（ \(r\) )和要赋的值（ \(v\) ）。赋值时，把左右端点split一下，然后将中间的部分变成一个新的区间即可。

void assign(int l,int r,int v){
	iit rr=split(r+1);
	iit ll=split(l);
	s.erase(ll,rr);
	s.insert(odt(l,r,v));
}

其他没啥好讲的了（真没啥能讲的了，一个比一个暴力，没脸讲）

那就再粘个区间加的代码吧（其他都是依葫芦画瓢了）

全取出来加一遍，完事（就这么简单粗暴）。

void add(int l,int r,int v){
    iit ll=split(l);
	iit rr=split(r+1);
    for(iit it=ll;it!=rr;it++)
		(it->v)+=v;
}

留道最简单的板子题吧

code

行了我知道你在找什么