线段树优化建图

一个很好用的 \(trick\)。

我们通过例题 CF786B 为例。

他需要我们支持点之间连边，点和区间之间连边，区间和点之间连边。

支持最短路。

如果我们暴力连边，显然最多是有 \(n^2\) 条边的。那怎么办呢，引入线段树分治。

线段树分治

在某些题中，我们可能会用 \(v \to u\in[l,r]\) 这种一个点指向区间，或者 \(u \in [l,r] \to v\) 这种东西。显然的,对于一个长度为 \(n\) 的序列，可能就会有 \(n^2\) 种边，直接存储肯定是不可以的。所以我们考虑用的东西优化建边。

如何优化建边？本质上的需求是用少量的点表示区间的边。就好比，我们读书的时候有一页页的页码，但是我们往往是通过章节来锁定内容；找章节的时候，我们有通过目录；找目录，我们通过找书...以此类推，我们可以发现，我们刚刚的例子，本质上就是用少量的点表示了区间的信息，也就是说，我们钦定点 \(v\) 表示一段区间，在钦定 \(u\) 表示一段点 \(v\)。这是什么？这显然就是树结构。

问题再次转化为，在树结构表示下，怎么用尽可能少的点表示出刚好是 \([l,r]\) 区间的所有点呢？显然是用类似线段树的方法，用 \(\log n\) 的区间表示，这样原本 \(n\) 的边数就优化为了 \(\log n\) 。对于点 \(u\) 连接区间 \([l,r]\) ，我们就相当于\(u\) 连接到了线段树上的区间，就像这个样子。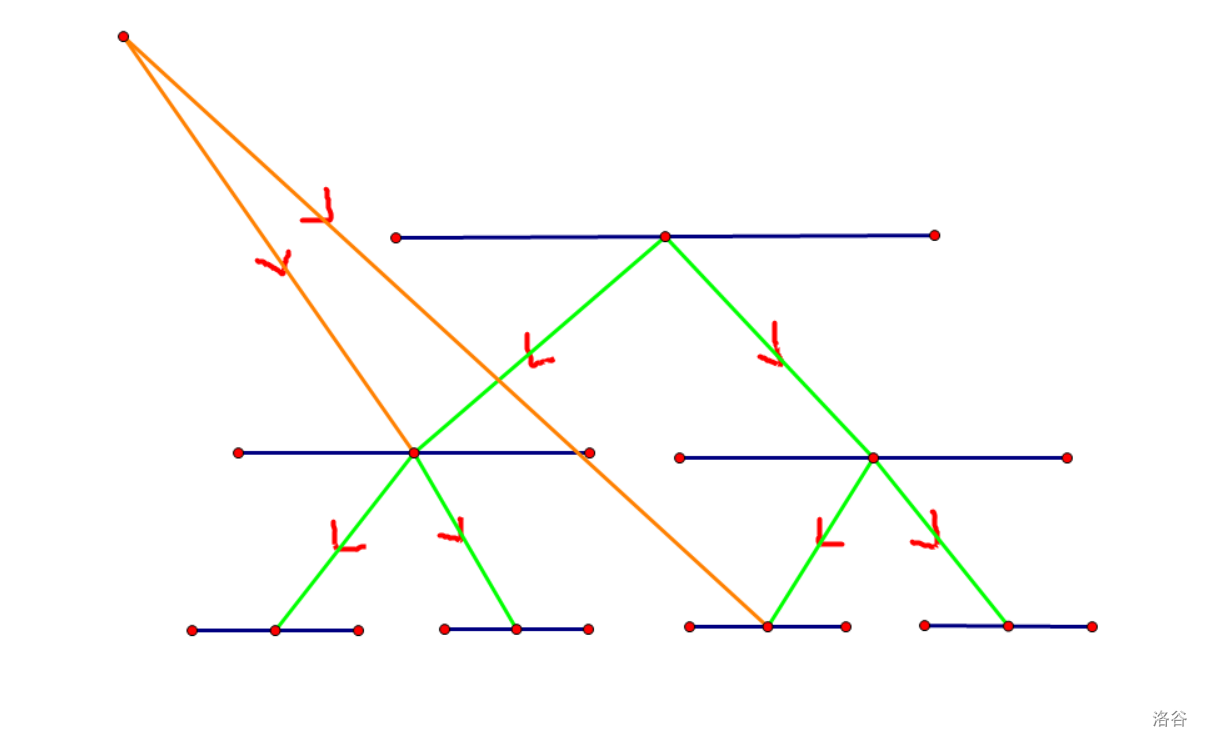

区间连点也是一样的。另外记得线段树上的点本身也要连边。不同的树也要连边，最后的效果就是这样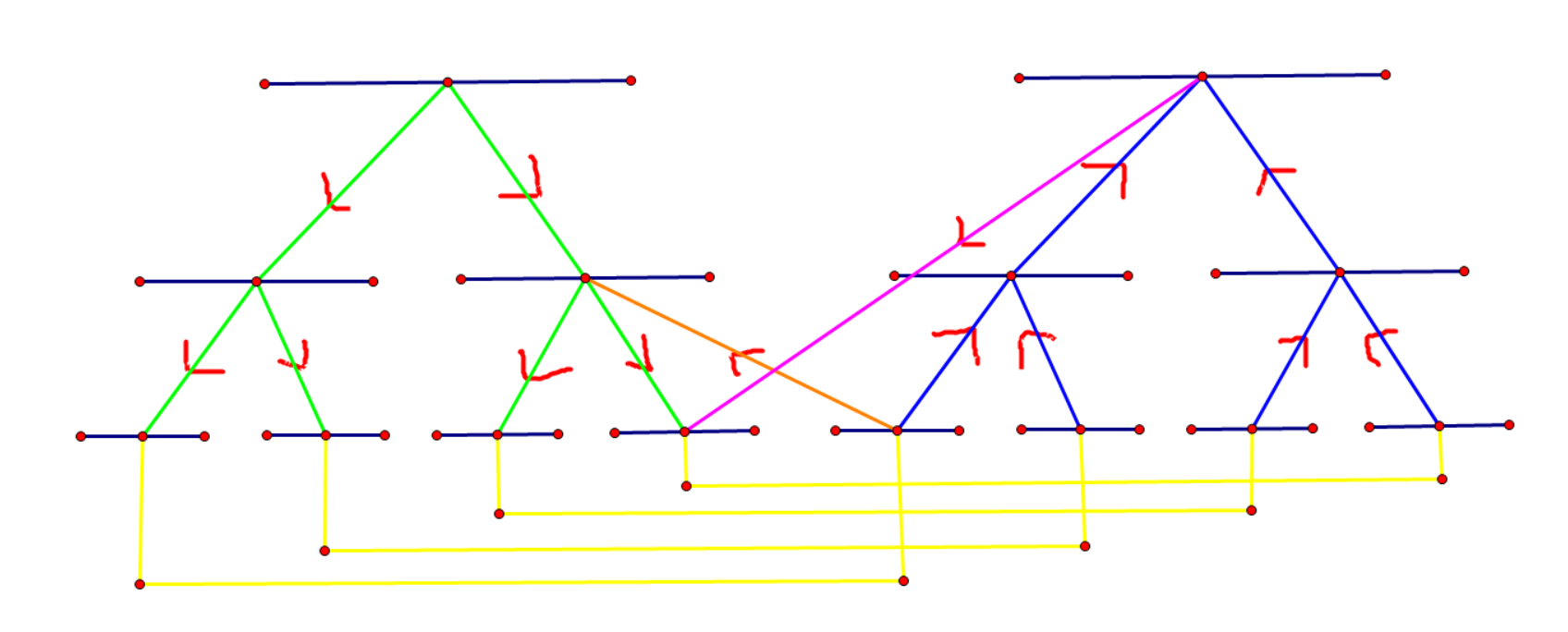

为什么要同时要用两棵树一个管出，一个入呢？我们用例题 CF786B 为例，你不可能说因为原来树上点到点距离为 \(0\)，所以最短路为 \(0\) 吧。