name title details created_date
lldxjw P7154&CF1778F&CF1276D&P8863 #P7154&CF1778F&CF1276D&P8863
P7154
题意
有两个长度为 \(N\) 的数列 \(s\) 和 \(t\)。
对于每个 \(s_i\) 都尝试与 \(t\) 中的元素进行匹配, \(s_i\) 与 \(t_j\) 能够匹配当且仅当 \(s_i \le t_i\) 。
我们称一个匹配时极大的,当且仅当未配对的 \(s_i\) 不能与任何一个未配对的 \(t_i\) 成功匹配。
计算极大的匹配的数量模 \(10^9+7\) 的结果。
$ N \le 3000,1\le s_i,t_i \le 10^9$
题解
显然这个极大的限制不是很好处理。
我们先搞一个显然但是正确性不对的做法。
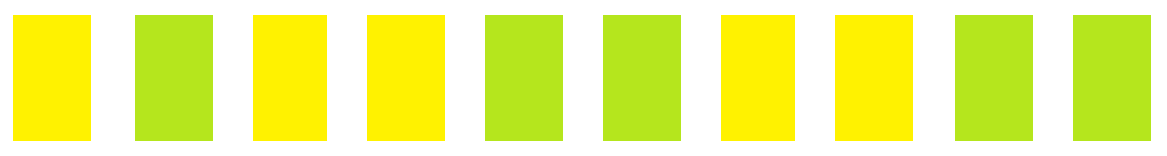
我们画一个图,其中黄色是牛棚,绿色是牛。
我们设 \(f_{i,j}\) 为考虑到第 \(i\) 个元素(此处指牛或牛棚),有 \(j\) 头牛还未被匹配。
牛的转移
CF1778F
题意
你有一颗有根树,有 \(n\) 个节点,编号为 \(1\) ~ \(n\)。
第 \(i\) 个顶点的权值是 \(a_i\) 你可以进行以下操作:
选择一个之前没选过的节点 \(v\) ,以及一个正整数 \(x\) ,需要满足 \(x\) 是 \(v\)子树内所有点的权值的公约数,然后令所有 \(v\) 子树内的节点的权值都乘 \(x\) 。
问在操作 \(\le k\)次后 \(a_1\) 的最大可能值是多少?
\(k \le n \le 10^5,a_i \le 1000\)。
CF1276D
题意
给定一棵\(n\)个点的树,点编号\(1 \sim n\),第\(i\)条边连接\(a_i\)和\(b_i\)。
初始时你有一个空的序列,树上的\(n\)个点都有标记。
现在按照边的编号从小到大考虑每一条边:
- 如果这一条边连接的两个点都有标记,则选择其中的一个点,擦除它的标记并将它的编号放入序列的末端;
- 否则什么都不做。
求能够由上述操作得到的不同的序列数量\(\bmod\ 998244353\)。
你有一个长度是 \(2^n\) 的序列 \(a\) , 下标从 \(1\) 到 \(2^n\) . ( \(n \le 18\) , \(-10^9 \le a_i \le 10^9\) ) .
你需要对这个序列进行 \(q\) ( \(q \le 2 \times 10^5\) ) 次操作 , 每次操作你都会得到一个整数 \(k\) ( \(0 \le k \le n-1\) ) . 你需要进行如下操作 :
- 对于 \(\forall i \in [1,2^n-2^k]\) , 如果 \(a_i\) 已经被交换过了 , 那么忽略它 ; 否则 , 将 \(a_i\) 和 \(a_{i+2^k}\) 进行交换 .
- 在这之后 , 输出序列最大子段和 . 本题中 , 最大子段可以一个数都不选 .
注意 , 每次操作之后不会撤销 .
「KDOI-03」构造数组
题意
你现在有一个长度为 \(n\) 的数组 \(a\)。一开始,所有 \(a_i\) 均为 \(0\)。给出一个同样长度为 \(n\) 的目标数组 \(b\)。求有多少种方案,使得通过若干次以下操作,可以让 \(a\) 数组变成 \(b\)。
- 选出两个不同的下标 \(1\leq i<j\leq n\),并将 \(a_i\) 和 \(a_j\) 同时增加 \(1\)。
两种方案被称之为不同的,当且仅当存在一个 \(x\) 使得一种方案中第 \(x\) 次操作选择的两个下标 \((i,j)\) 与另一种方案中的不同。
答案对 \(\bmod\ {998244353}\) 取模。
对于 \(100\%\) 的数据,\(1\le n\le5~000\),\(1\leq b_i\le30~000\),\(\sum b_i\le30~000\)。
题解
我们可以将这个拍到平面上。
设行 \(x\) 为操作,列 \(y\) 为物品种类。
对于每一次操作,相当于选择两列放置两粒棋子。
结果就是对于每一行有2粒棋子,每一列有\(a_i\)粒棋子。
按列考虑,记 \(f_{i,j,k,l}\) 为考虑前 \(i\) 列,有 \(j\) 行有 \(0\) 个棋子,有 \(k\) 行有 \(1\) 个棋子,有 \(l\) 行有 \(2\) 个棋子。
对于每一列,我们考虑枚举一个 \(u\) ,表示有 \(u\) 个棋子放在了 \(0\) 个棋子的行,有 \(a_i-u\) 放在了 \(1\) 个棋子的行。
我们会发现这个状态数好大啊,所以我们要降维。
观察发现
通过这两个式子,我们可以用一个变量表示另外两个变量。
2023-08-09 09:22:48
lldxjw qwq # qwq
计算时间复杂度时,我们可以考虑将其与一个数字串一一对应起来计算
至少有一个B->全集-全是A 2023-08-10 08:48:30
lldxjw CF1363F # CF1363F
CF1363F Rotating Substrings
题面
给定两个长度为 \(n\) 的字符串 \(s\),\(t\)。定义一次操作为选择 \(s\) 的一个子串 \(s_{l, l +1, \dots, r}\),然后将之修改为 \(s_{r, l, l + 1, l + 2, \dots, r - 1 }\)。请求助使 \(s\) 与 \(t\) 相等的最小操作次数。无解输出 \(-1\)。
多组数据,\(\sum n \leq 2000\),\(s, t\) 中只有小写字母。
题解
2023-08-10 19:52:31
lldxjw 球盒问题 ## 球盒问题
n个球,m个盒子
球本质不同,盒子本质不同,能有空
球本质不同,盒子本质不同,不能有空
球本质不同,盒子本质相同,不能有空
球本质不同,盒子本质相同,能有空
球本质相同,盒子本质不同,不能有空
球本质相同,盒子本质不同,能有空
球本质相同,盒子本质相同,不能有空
球本质相同,盒子本质相同,能有空
2023-08-11 08:13:23
lldxjw 计数问题 # 计数问题
球盒问题
n个球,m个盒子
- 球本质不同,盒子本质不同,不能有空(考虑容斥,2. 减去不合法的方案)
- 球本质不同,盒子本质不同,能有空(考虑球选盒子,共有 \(m^n\) 种)
- 球本质不同,盒子本质相同,不能有空(考虑1.,并去掉m个盒子之间的顺序,为第二类斯特林数)
- 球本质不同,盒子本质相同,能有空(枚举用了几个盒子,对第二类斯特林数进行前缀和)
注意:此处不能直接将 2. 除以 \(m!\) ,对于两个空盒子,交换他两个是没有任何区别的。 - 球本质相同,盒子本质不同,不能有空(插板 \(C_{n-1}^{m-1}\))
- 球本质相同,盒子本质不同,能有空(插板 \(C_{n+m-1}^{m-1}\) )
zhq的解释:考虑n个球,补上m-1个球,然后将其中的m-1个变成隔板。 - 球本质相同,盒子本质相同,不能有空(dp有序枚举)
设G[n][m]表示,n个球,放到m个盒子里的方案数。
DP的转移,往往可以看做“分类讨论”的过程。这个DP,我们分“是否有空盒子”进行转移。
G[n][m] = G[n][m - 1] + G[n - m][m] - 球本质相同,盒子本质相同,能有空(修改结束状态 G[n-m][m])
2023-08-11 21:12:11
lldxjw 在此处输入标题 $$\lfloor \frac{\lfloor \frac{x}{y_1} \rfloor }{y_2} \rfloor \
\lfloor \frac{x}{y_1 y_2} \rfloor $$
森林的连通块个数:点数-边数 2023-08-12 09:02:39
lldxjw 点分治 点分树 # 点分治 点分树
坏了这个真快学傻了。
普通的分治,大概就是将整个序列平均分成两份,
整体二分
2023-08-15 09:42:48
lldxjw 在此处输入标题 设有一条边x->y
在最短路径中,若一条边x到终点不经过当前边,那么其他点也不经过这条边
编号为1号点的强连通分量出度为0 2023-08-16 14:56:59
lldxjw 在此处输入标题 欧拉序(O1求LCA)
欧拉序是在递归过程中每遇到一个节点就加入序列
找x,y两点的lca
就是在欧拉序的两点间找深度最小的点。
欧拉序将树上问题转换成区间问题,我们可以用st表求解。
克鲁斯卡尔重构树
找最小生成树,将树上边权建立一个新点,连接这条
强联通分量
dfn表示遍历到当前点的时间戳,low表示能遍历到的dfn最小的点的时间戳
遍历时压栈,当dfn=low时弹栈
若v不在栈中,则不是强联通分量。
点双
边双
2023-08-17 08:39:25
lldxjw include<bits/stdc++.h> "图上问题->树上问题->序列问题
连通分量专题
强连通分量(SCC)
对于一个有向图,当其中任意两点都能互相到达时,我们认为这是强联通的
int dfn[N],low[N],belong[N],cnt,tot;
bool instack[N];
vector<int>scc[N];
stack<int>st;
void dfs(int u){
dfn[u]=low[u]=++cnt;
st.push(u);instack[u]=1;
for(int i=head[u];i;i=nxt[i]){
int v=to[i];
if(!dfn[v]){
dfs(v);
low[u]=min(low[u],low[v]);
}else if(instack[v])low[u]=min(low[u],low[v]);
//v has gone to u,u can also to v
}
if(low[u]==dfn[u]){
++tot;
while(st.top()!=u){
belong[st.top()]=tot;
instack[st.top()]=0;
scc[tot].push_back(st.top());
st.pop();
}
belong[u]=tot;
scc[tot].push_back(st.top());
instack[u]=0;
st.pop();
}
}
双联通分量(BCC)
双联通分量仅存在于无向图
在一张连通的无向图中,对于两个点 u 和 v,如果无论删去哪个点(只能删去一个,且不能删 u 和 v 自己)都不能使它们不连通,我们就说 u 和 v 点双连通。
边双
边双连通具有传递性
在无向图中,对于任意两个点 u 和 v,如果无论删去哪条边都不能使它们不连通,我们说该图边双联通。
点双
点双连通不具有传递性
在无向图中,对于任意两个点 u 和 v,如果无论删去哪个点都不能使它们不连通,我们说该图点双联通。
void dfs(int u,int fa){
int son=0;
dfn[u]=low[u]=++cnt;
st.push(u);
for(int i=head[u];i;i=nxt[i]){
int v=to[i];
if(!dfn[v]){
son++;
dfs(v,u);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]){
++tot;
while(st.top()!=v){
bcc[tot].push_back(st.top());
st.pop();
}
bcc[tot].push_back(st.top());
st.pop();
bcc[tot].push_back(u);
//因为u可能同时也在别的点双联通分量中,所以不能直接pop(u)
//因为栈内还存在别的双联通分量,所以只pop到v
}
}else if(v!=fa)low[u]=min(low[u],dfn[v]);
}
if(!fa&&!son)bcc[++tot].push_back(u);
}
割点
对于一点u,若删掉u,连通块数量增加1,则该点为割点
对于割点,我们可以发现,割点dfs子树内的任意一个点,都访问不到割点的祖先节点。
所以如果子节点的low大于等于当前点,则当前点为割点
(要特判当前点是root的情况,防止你是链的端点)
割边
对于一条边e,若删掉e,连通块数量增加1,则该点为割边
对于割边,我们可以发现,割边dfs子树内的任意一个点,都访问不到割边的祖先节点。
所以如果子节点的low大于等于当前点,则当前边为割边
(要特判当前点是root的情况,防止你是链的端点)
2-SAT问题
有若干的要求 \(x_1\)成立 或 \(x_2\) 成立, \(x_3\)不成立 或 \(x_4\) 成立
条件1我们可以转化成 \(A\Rightarrow!B\) 和 \(B\Rightarrow!A\)。
条件2我们可以转化成 \(!A\Rightarrow!B\) 和 \(B\Rightarrow A\)。
对于每个数值我们建两个点,表示该条件成立或不成立。
若 \(A\) 经过若干点指向 \(!A\) ,且 \(!A\) 经过若干点指向 \(A\) ,则该条件不成立。
因为可能 \(A\Rightarrow !A\) 但是 \(!A\not\Rightarrow A\),所以我们从编号小的强联通分量开始选。
(是否可以搞3-SAT?)
" 2023-08-18 09:27:51
lldxjw 图论 # 图论
前后缀优化建图
线段树优化建图
2023-08-18 16:10:51
lldxjw 实用链接 "废话: 数论这个东西,好像学了,又好像没学,或许是我不配了(来自复习中的lyk) 。
小声bb:由于工期过长,前后文风格都不统一了,麻了。
花絮:麻了有好多东西都丢了……机房电脑被我清的一干二净,QQ发手机上又忘下载,崩大溃。
实用链接
目录
质数与约数
素数判断及筛法
试除法
若有一个正整数 \(n\) 为合数,则存在一个能整除 \(n\) 的数 \(d\),且 \(2\le d \le \sqrt{n}\) 。因此我们只需要扫描 2 ∼ \(n\) 之间的所有整数,依次检查它们能否整除 n,若都不能整除,则 n 为质数,否则 n 为合数。注意,我们还需要特判 0 和 1 这两个整数。
时间复杂度 \(O(\sqrt n)\) 。
bool is_prime(int n){
if(n<2)return false;
for(int i=1,sq=sqrt(n);i<=sq;i++){
if(n%i==0)return false;
}
return true;
}
埃氏筛
对于每个质数 \(p\) 而言,小于 \(p^2\) 的 \(p\) 的倍数在扫描到更小的质数时就已经被标记过了。
于是从 \(p^2\) 开始扫。
void found_prime() {
memset(vis, 0, sizeof(vis));
vis[0] = 1; vis[1] = 1; // 特殊处理 0 和 1
for(int i=2; i<=n; ++i) {
if(!vis[i]) { // i 为质数
for(int j=i*i; j<=n; j+=i)
vis[j] = 1; // 标记合数
}
}
}
线性筛
#include<bits/stdc++.h>
using namespace std;
const int N=1e8+50;
int prime[N],cnt;
bool vis[N];
int n,q;
void init(){
for(int i=2;i<=n;i++){
if(!vis[i])prime[++cnt]=i;
for(int j=1;j<=cnt&&prime[j]<=n/i;j++){
vis[i*prime[j]]=1;
if(i%prime[j]==0)break;
}
}
}
int main(){
scanf("%d%d",&n,&q);
init();
while(q--){
int x;
scanf("%d",&x);
printf("%d\n",prime[x]);
}
}
素性测试
算数基本定理
算术基本定理又名唯一分解定理,任何一个大于 1 的正整数都能唯一分解为若干个质数的乘积。
(这东西太简单就不证了吧)
推论1: \(n\) 的正约数个数为:
\[(c_1+1)\times(c_2+1)\times\cdots\times(c_m+1)=\prod_{i=1}^{m}(c_i+1) \]推论2: \(n\) 的所有正约数的和为:
\[(1+p_1+p_1^2+\cdots +p_1^{c_1})\times\cdots\times(1+p_m+p_m^2+\cdots +p_m^{c_m})=\prod_{i=1}^m(\sum_{j=0}^{c_i}(p_i)^j) \]经典题摘录
P1463 反素数
首先我们知道:
在12e9范围内,1N中任何数的不同质因子都不会超过10个,且所有质因子的指数总和不超过30(证明)
并且,这个数想要成为反素数,则
\[c_1\ge c_2\ge c_3\ge c_4\ge c_5\ge c_6\ge c_7\ge c_8\ge c_9\ge c_{10} \]若质数不单调递减,则必有一个小于他的数,约数个数等于他。
由于需要枚举的数极小,且很快衰减成0,所以直接dfs即可。
T311325 gcd与lcm
显然,对于两个数的gcd和lcm,$\gcd| \operatorname{lcm} $ 且 \(\frac{a}{\gcd}\)与 \(\frac{b}{\gcd}\) 互质。
于是直接枚举lcm/gcd的约数,判断第一个满足条件的即可。
Neko does Maths
不想写了,直接挂个题解吧(另:挺经典的,要认真看!)。
整除分块
可以先看一下开头的实用链接。
大概就是,由于一部分区域的答案是相同的,我们就把他们划分到同一个块内,统一计算。
经典题摘录
P14053 [AHOI2005]约数研究
不是很会描述,还是挂题解吧(我真菜啊连整除分块都讲不了……)
P2261 [CQOI2007]余数求和
由 \(a\bmod b=a-\lfloor \frac{a}{b}\rfloor\times b\)
\[\sum_{i=1}^n k \bmod i\\ \sum_{i=1}^n k-\lfloor \frac{k}{i}\rfloor\times i\\ n\times k-\sum_{i=1}^n \lfloor \frac{k}{i}\rfloor\times i \]其中 \(\lfloor \frac{k}{i}\rfloor\) 可整除分块。
Floor and Mod
好题,挂题解吧。
P3935 Calculating
题解也懒得挂了系列……。
P1072 [NOIP2009 提高组] Hankson 的趣味题
大小型分类讨论,但感觉也不错。
欧拉函数
参考文章:
定义
我们定义 \(\varphi(x)\) 为 小于 \(x\) 的正整数中与 \(x\) 互质的数的个数,称作欧拉函数。
性质
-
若 \(x\) 为质数, \(\varphi(x)=x-1\)
证明:显然若 \(x\) 是质数,在1 ~ \(x\) 范围内,除 \(x\) 本身外,其余数字均与 \(x\) 互质。
-
若 \(x=p^c\) ( \(p\) 为质数),则 \(\varphi(x)=(p-1) \times p^{k-1}\) 。
证明:所有 \(p\) 的倍数都与 \(x\) 不互质,其他所有数都与他互质。\(p\) 的倍数刚好有 \(p^{k-1}\) 个(包括 \(x\) 本身)
那么 \(\varphi(x)=p^k-p^{k-1}=(p-1)\times p^{k-1}\) 。
-
若 \(p,q\) 互质,则有 \(\varphi(p\times q)=\varphi(p)\times \varphi(q)\) ,可知,欧拉函数本身是积性函数。
-
若 \(p\) 为 \(x\) 的约数( \(p\) 为质数, \(x\) 为任意正整数),我们有 \(\varphi(x\times p)=\varphi(x)\times p\)
-
若 \(p\) 不为 \(x\) 的约数( \(p\) 为质数, \(x\) 为任意正整数),我们有 \(\varphi(x\times p)=\varphi(x)\times (p-1)\)
-
对于一个正整数 \(x\) 的质数幂分解 $$x=p_1^{k1}\times p_1^{k1}\times\cdots\times p_1{k1}=\prod_{i=1}n p_i^{k_i}$$ 。
\[\varphi(x)=x\times (1-\frac{1}{p_1} ) \times (1-\frac{1}{p_1} ) \times\cdots\times (1-\frac{1}{p_1} ) = x\times \prod_{i=1}^{n}(1-\frac{1}{p_i}) \]
求欧拉函数
若求单个数的欧拉函数,直接利用性质4求解。时间复杂度\(O(\sqrt x)\)。
int phi(int n) {
int ans = n;
int t = sqrt(n);
for(int i=2; i<=t; ++i) {
if(n%i == 0)
ans = ans/i*(i-1);
while(n%i == 0) n /= i;
}
if(n > 1) ans = ans/n/(n-1);
return ans;
}
若求前\(n\)个数的欧拉函数,可使用埃氏筛(性质4)或线性筛(性质5、6)。
//线性筛
void init(){
int n=1e7+50;//范围
phi[1]=1; //特判1
for(int i=2;i<=n;i++){
if(!vis[i]){pr[++cnt]=i,phi[i]=i-1;}//质数,性质1
for(int j=1;j<=cnt&&pr[j]<=n/i;j++){
vis[i*pr[j]]=1;
phi[i*pr[j]]=phi[i]*((i%pr[j])?pr[j]-1:pr[j]);
if(i%pr[j]==0)break;
}
}
}
经典题摘录
P2303 [SDOI2012] Longge 的问题
费马小定理
如果 \(p\) 是质数,则对任意整数 \(a\) ,有
\[a^p\equiv a(\bmod\ p)\Rightarrow \gcd(a,p)=1 \]前提:
- \(p\) 是质数
- \(gcd(a,p)=1\)
证明:
有数列\(S=\{1,2,3,\cdots p-1\}\),将 \(S\times a \Rightarrow \{a,2a,3a,\cdots,(p-1)a\}\)
\[(S\times a)\bmod\ p\ \Rightarrow\ \{a,2a,3a,\cdots,(p-1)a\}\bmod\ p\Rightarrow \{1,2,3,\cdots,p-1\} \](因为 \(\gcd(a,p)=1\),所以余数为1~p-1)
\[\prod_{i=1}^{p-1}i\equiv\prod_{i-1}^{p-1}a\times i\pmod p\\ (p-1)!\equiv a^{p-1}\times(p-1)!\pmod p\\ 1\equiv a^{p-1}\pmod p\\ a^{-1}\equiv a^{p-2}\pmod p\\ \]欧拉定理
gcd
设 \(a=bk+c\),显然有 \(c=a \bmod b\)。设 \(d \mid a,~d \mid b\),则 \(c=a-bk, \frac{c}{d}=\frac{a}{d}-\frac{b}{d}k\)。由右边的式子可知\(\frac{c}{d}\) 为整数,即 \(d \mid c\) ,所以对于 \(a,b\) 的公约数,它也会是 \(b,a \bmod b\) 的公约数。反过来也需要证明:设 \(d \mid b,~d\mid (a \bmod b)\),我们还是可以像之前一样得到以下式子 \(\frac{a\bmod b}{d}=\frac{a}{d}-\frac{b}{d}k,~\frac{a\bmod b}{d}+\frac{b}{d}k=\frac{a}{d}\) 。因为左边式子显然为整数,所以 \(\frac{a}{d}\) 也为整数,即 \(d \mid a\),所以 \(b,a\bmod b\) 的公约数也是 \(a,b\) 的公约数。既然两式公约数都是相同的,那么最大公约数也会相同。所以得到式子
exgcd
设 \(ax_1+by_1=\gcd(a,b)\),\(bx_2+(a\bmod b)y_2=\gcd(b,a\bmod b)\)
由欧几里得定理可知: \(\gcd(a,b)=\gcd(b,a\bmod b)\)
所以 \(ax_1+by_1=bx_2+(a\bmod b)y_2\)
又因为 \(a\bmod b=a-(\lfloor\frac{a}{b}\rfloor\times b)\)
所以
因为 \(a=a,b=b\) ,所以 \(x_1=y_2,y_1=x_2-\lfloor\frac{a}{b}\rfloor y_2\)
将 \(x_2,y_2\) 不断代入递归求解直至 \(\gcd\) (最大公约数,下同)为 \(0\) 递归 \(x=1,y=0\) 回去求解。
设 \(x_0,y_0\) 为 \(ax+by=\gcd(a,b)\) 的一组特解。
设 \(x_1=\frac{x_0 c}{\gcd(a,b)}~y_1=\frac{y_0 c}{\gcd(a,b)}\)
则 \(x_1,y_1\) 为 \(ax+by=c\) 的一组特解
设任意 \(d\in Q\) ,那么
同时, \(x_1+db\) 与 \(y_1-da\) 需均为正数。
因为 \(x_1,y_1\in \text{Z}\)
所以我们需要 \(da\in \text{Z},db \in \text{Z}\) 。
当 \(d\) 取到最小可能的正值时 \(d_x=db,d_y=da\) 那么任意解中这两个变量与 \(x_1,y_1\) 的偏差一定分别是 \(d_x\) 和 \(d_y\) 的倍数。
显然最小时 \(d_x=\frac{b}{\gcd(a,b)}\),\(d_y=\frac{a}{\gcd(a,b)}\) ,在 \(d=\frac{1}{\gcd(a,b)}\) 时取到
通解公式
\(s\) 是任意整数
两条性质:
- \(x\) 增大时 \(y\) 减小
- \(s\) 越大, \(x\) 越大, \(y\) 越小。
若我们限制 \(x>0\) 有 \(x_1+s d_x>0,s>-\frac{x_1}{d_x}\)
若我们限制 \(y>0\) 有 \(y_1-s d_y>0,s<\frac{y_1}{d_y}\)
所以 \(-\frac{x_1}{d_x}<s<\frac{y_1}{d_y}\)
因为 \(s\) 是整数,故
杂项
等比数列:\(S_n=a_0\frac{q^n-1}{q-1}\)
n以内质数个数大概是 \(\frac{n}{\ln\ n}\),插一条证明(虽然这篇文章大部分都是在讲别的……)
在12e9范围内,1N中任何数的不同质因子都不会超过10个,且所有质因子的指数总和不超过30
证明:
因为最小的11个质数的乘积大于2e9,且2^31>2e9,所以成立
\(a\bmod b=a-\lfloor \frac{a}{b}\rfloor\times b\)
调和级数" 2023-08-20 11:46:19
lldxjw 在此处输入标题 $$\because ax+by=c\
\therefore\gcd(a,b)\mid (ax+by)\
\therefore \text{if}~ \gcd(a,b) \not \mid c\Rightarrow \text{No solution}$$
设 \(x_0,y_0\) 为 \(ax+by=\gcd(a,b)\) 的一组特解。
设 \(x_1=\frac{x_0 c}{\gcd(a,b)}~y_1=\frac{y_0 c}{\gcd(a,b)}\)
则 \(x_1,y_1\) 为 \(ax+by=c\) 的一组特解
设任意 \(d\in Q\) ,那么
同时, \(x_1+db\) 与 \(y_1-da\) 需均为正数。
因为 \(x_1,y_1\in \text{Z}\)
所以我们需要 \(da\in \text{Z},db \in \text{Z}\) 。
当 \(d\) 取到最小可能的正值时 \(d_x=db,d_y=da\) 那么任意解中这两个变量与 \(x_1,y_1\) 的偏差一定分别是 \(d_x\) 和 \(d_y\) 的倍数。
显然最小时 \(d_x=\frac{b}{\gcd(a,b)}\),\(d_y=\frac{a}{\gcd(a,b)}\) ,在 \(d=\frac{1}{\gcd(a,b)}\) 时取到
通解公式
\(s\) 是任意整数
两条性质:
- \(x\) 增大时 \(y\) 减小
- \(s\) 越大, \(x\) 越大, \(y\) 越小。
若我们限制 \(x>0\) 有 \(x_1+s d_x>0,s>-\frac{x_1}{d_x}\)
若我们限制 \(y>0\) 有 \(y_1-s d_y>0,s<\frac{y_1}{d_y}\)
所以 \(-\frac{x_1}{d_x}<s<\frac{y_1}{d_y}\)
因为 \(s\) 是整数,故
2023-08-20 19:59:21
lldxjw 在此处输入标题 树状数组边修边查(笑哭)
输出忘记排序(这个可以想到的时候记在代码的注释里) 2023-08-21 16:04:40