趁着 opj 让刷数据结构的理由赶紧水几道入门的分块题。。。
以下 \(n\) 一般为序列长度,\(m\) 为询问次数,\(V\) 为值域。
你的名字
真心觉得有黑。下面俩题跟这个一比,简直是萌萌题。
细节太多,难实现。
题意:
给定一个长为 \(n\) 的序列,每次询问区间 \([l,r]\) 模 \(k\) 意义下的最小值。
\(n\leq 3\times 10^5\),\(k,V \leq 10^5\)。
1s,128MB ~ 256MB。
乘法相关,根号分治。
考虑一个阈值 \(T\),先考虑 \(k < T\)。
-
暴力构造 \(b_i=a_i \bmod k\),然后 RMQ 即可,这里干脆直接分块维护。
-
复杂度 \(O(nT+m\sqrt n)\)。
下面考虑 \(k \geq T\) 的情况。
枚举 \(k\) 的倍数 \(p\),对于每个 \(p\),询问 \(\min\{ a_i \mid l\leq i \leq r \wedge a_i \geq p \}-i\),再对所有 \(p\) 的这个最小值取 min,即为答案。
有个 \(a_i \geq p\) 的限制,考虑把所有 \(p\) 排序,从大到小枚举 \(p\) 的同时,把数组中 \(\geq p\) 的值插入。
思考如何维护插入 \(n\) 个数,处理 \(\frac{mV}{T} \approx m\sqrt V\) 次询问。
询问次数太多,需要做到每次询问 \(O(1)\)。不难想到猫树或者 ST 表。
但猫树更新一个值是 \(O(n)\) 的,ST 表为 \(O(n\log n)\)。
虽然 ST 表带一个 log,但常数极小,而且比猫树好写得多,于是考虑改进 ST 表。
考虑分块,每个块维护前缀后缀 min,然后对所有块的最小值 ST 表。
那么中间一大截整的块就可以用 ST 表 \(O(1)\) 维护最小值,不完整的块用前缀后缀 min 维护,每次查询 \(O(1)\) 不变。
每次修改 \(O(L+\frac{n}{L}{\log_\frac{n}{L}})\)。
但会发现这无法处理 \(l,r\) 在同一个块里的情况,但都在同一个块了,你为什么不暴力呢?
然后还有个致命的问题:如果存下所有 \(p\),空间会炸。
考虑从 \(v \sim 1\) 枚举 \(k'\),每次考虑 \(k'\) 对其因子的贡献即可。
卡常技巧
- 对于每一个 \(k\),估算一下两种做法的时间复杂度,选小的。
- 尽量不要用取模。
代码细节很多。
#include<bits/stdc++.h>
using namespace std;
const int N=3e5+5,M=1e5+5,inf=N;
int n,m,V,a[N],ans[N],L[N],R[N],vis[M],ans2[N];
//L[i]~R[i] 存储一段 k 相同的区间。
//ans2:对于第二种情况 l,r 在同一个块的情况
//注意上述两种情况都是对一整个 k 相同的区间操作的,所以对于单个询问的特殊处理需要单独记一下。
struct node{int l,r,k,id;} q[N];
void ckmin(int &x,int y) {if(y<x) x=y;}
char buf[1<<15],*p1=buf,*p2=buf;
#define nc() (p1==p2&&(p2=buf+fread(p1=buf,1,1<<15,stdin),p1==p2)?-1:*p1++)
inline int rd()
{
int x=0,f=1;char c=nc();
for(;!isdigit(c);c=nc()) if(c=='-') f=-1;
for(; isdigit(c);c=nc()) x=(x<<3)+(x<<1)+(c^48);
return x*f;
}
namespace solve1//构造 bi=ai%k 的做法
{
const int T=550;
int v[N],c[N],mn[N/T+5];
int query(int l,int r)
{
int ans=inf;
if(l/T==r/T) {for(int i=l;i<=r;i++) ans=min(ans,v[i]);return ans;}
int L=l/T*T+T-1,R=r/T*T;
for(int i=l;i<=L;i++) ans=min(ans,v[i]);
for(int i=R;i<=r;i++) ans=min(ans,v[i]);
for(int i=l/T+1;i<R/T;i++) ans=min(ans,mn[i]);
return ans;
}
void solve(int k)
{
for(int i=0;i<k;i++) c[i]=i;
for(int i=k;i<=V;i++) c[i]=c[i-k];
//不取模处理每个数 %k 的值
for(int i=1;i<=n;i++) v[i]=c[a[i]];
for(int i=0;i<=n/T;i++) mn[i]=inf;
for(int i=0;i<=n/T;i++)
{
int L=max(1,i*T),R=min(n,i*T+T-1);
for(int j=L;j<=R;j++) mn[i]=min(mn[i],v[j]);
}
for(int i=L[k];i<=R[k];i++) ans[q[i].id]=query(q[i].l,q[i].r);
}
}
namespace solve2
{
const int T=550,Lg=10;
int st[Lg][N/T+5],lmn[N],rmn[N],lg[N/T+5];
vector<int> v[M];
void upd(int p,int x)
{
//维护 前后缀数组
//由于是从大到小插,可以直接复制
int bel=p/T,L=max(1,bel*T),R=min(n,bel*T+T-1);
for(int i=L;i<=p;i++) rmn[i]=x;
for(int i=p;i<=R;i++) lmn[i]=x;
//维护 st 表
st[0][bel]=x;
for(int i=1;i<Lg;i++)
{
int L=max(0,bel-(1<<i)+1),R=min(bel,n/T-(1<<i)+1);
for(int j=L;j<=R;j++) st[i][j]=x;
}
}
int query(int l,int r)
{
int L=l/T+1,R=r/T-1,t=lg[R-L+1];
return min(min(lmn[r],rmn[l]),(L<=R?min(st[t][L],st[t][R-(1<<t)+1]):inf));
}
void solve()
{
for(int i=1;i<=n;i++) v[a[i]].push_back(i);
for(int i=2;i<=n/T;i++) lg[i]=lg[i>>1]+1;
for(int i=1;i<=n;i++) lmn[i]=rmn[i]=inf;
for(int i=0;i<Lg;i++) for(int j=0;j<=n/T;j++) st[i][j]=inf;
for(int i=V;i;i--)
{
for(int p:v[i]) upd(p,i);
for(int j=1;j*j<=i;j++)
if(i%j==0)
{
if(!vis[j]) for(int k=L[j];k<=R[j];k++) ckmin(ans[q[k].id],query(q[k].l,q[k].r)-i);
if(j*j!=i&&!vis[i/j]) for(int k=L[i/j];k<=R[i/j];k++) ckmin(ans[q[k].id],query(q[k].l,q[k].r)-i);
}
}
//注意 0 是所有数的倍数,最后还要再做一次
for(int i=1;i<=m;i++) ckmin(ans[q[i].id],query(q[i].l,q[i].r));
}
}
int main()
{
n=rd(),m=rd();
for(int i=1;i<=n;i++) V=max(V,a[i]=rd());
for(int i=1;i<=m;i++) q[i]={rd(),rd(),rd(),i};
sort(q+1,q+1+m,[&](node a,node b){return a.k<b.k;});
for(int i=1;i<=m;i++)
{
auto [l,r,k,id]=q[i];
ans[id]=ans2[id]=inf;
if(r-l<=550) for(int j=l;j<=r;j++) ckmin(ans2[id],a[j]%k);
if(!L[k]) L[k]=i;R[k]=i;
}
for(int i=1;i<=V;i++)
{
if(!L[i]) {vis[i]=1;continue;}
//粗略计算一下两种复杂度
if(n<1ll*(V/i)*(R[i]-L[i]+1)*3) solve1::solve(i),vis[i]=1;
}
solve2::solve();
for(int i=1;i<=m;i++) printf("%d\n",(ans2[i]==inf?ans[i]:ans2[i]));
}
由乃打扑克
喜欢我超强样例还不给下数据吗?
题意:
给定一个序列长为 \(n\),每次求区间第 \(k\) 小或者区间加上 \(x\)。
\(n \leq 10^5\),\(V\) 在 int 范围。
2s,128 MB。
一眼想到 \(n\sqrt n \log_{\sqrt n}\log_{V}\),没想到能过(
主席树之类的显然不能再维护一个区间加的操作,考虑分块。
先考虑如何分块求区间第 \(k\) 小。
- 可以二分第 \(k\) 小,统计 \(i\in[l,r] \wedge a_i \leq k\) 的个数。
- 对于每一块排序,满足单调性,即可二分每个块内满足条件数的个数,其余暴力判。
然后分块维护区间加就很容易了。
- 对于一整块加上 \(x\),显然不需要重新排序,打标记即可。
- 否则暴力加上后块内重新排序,显然每次操作最多两个块重新排序。
卡常技巧:
- 二分第 \(k\) 先求一边 \([l,r]\) 的最大最小值。
- 如果当前块最大值 \(\leq k\),或最小值 \(>k\),则不需要块内二分。
不清楚为什么这题还需要开 long long。
至于为什么这么简单调了一晚上,因为 TM 看错题了,二分边界赋小了。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5,T=200,inf=1e10;
int n,m,a[N],b[N],add[N/T+5],L[N],R[N],bel[N];
void ckmin(int &x,int y) {if(y<x) x=y;}
void ckmax(int &x,int y) {if(y>x) x=y;}
char buf[1<<15],*p1=buf,*p2=buf;
#define nc() (p1==p2&&(p2=buf+fread(p1=buf,1,1<<15,stdin),p1==p2)?-1:*p1++)
inline int rd()
{
int x=0,f=1;char c=nc();
for(;!isdigit(c);c=nc()) if(c=='-') f=-1;
for(; isdigit(c);c=nc()) x=(x<<3)+(x<<1)+(c^48);
return x*f;
}
void upd(int l,int r,int k)
{
int lb=bel[l],rb=bel[r];
if(lb==rb)
{
for(int i=l;i<=r;i++) a[i]+=k;
for(int i=L[lb];i<=R[lb];i++) b[i]=a[i];
sort(b+L[lb],b+R[lb]+1);
return;
}
for(int i=l;i<=R[lb];i++) a[i]+=k;
for(int i=L[lb];i<=R[lb];i++) b[i]=a[i];
sort(b+L[lb],b+R[lb]+1);
for(int i=L[rb];i<=r;i++) a[i]+=k;
for(int i=L[rb];i<=R[rb];i++) b[i]=a[i];
sort(b+L[rb],b+R[rb]+1);
for(int i=lb+1;i<rb;i++) add[i]+=k;
}
int qry(int l,int r,int op)
{
int ans=op?inf:-inf,lb=bel[l],rb=bel[r];
if(lb==rb) {for(int i=l;i<=r;i++) op?ckmin(ans,a[i]+add[lb]):ckmax(ans,a[i]+add[lb]);return ans;}
for(int i=l;i<=R[lb];i++) op?ckmin(ans,a[i]+add[lb]):ckmax(ans,a[i]+add[lb]);
for(int i=L[rb];i<=r;i++) op?ckmin(ans,a[i]+add[rb]):ckmax(ans,a[i]+add[rb]);
for(int i=lb+1;i<rb;i++) op?ckmin(ans,b[L[i]]+add[i]):ckmax(ans,b[R[i]]+add[i]);
return ans;
}
int qkth(int l,int r,int k)
{
if(k>r-l+1) return -1;
int lb=bel[l],rb=bel[r];
int vL=qry(l,r,1),vR=qry(l,r,0),ans;
while(vL<=vR)
{
int m=(vL+vR)>>1,c=0;
if(lb==rb) for(int i=l;i<=r;i++) c+=a[i]+add[lb]<=m;
else
{
for(int i=l;i<=R[lb];i++) c+=a[i]+add[lb]<=m;
for(int i=L[rb];i<=r;i++) c+=a[i]+add[rb]<=m;
for(int i=lb+1;i<rb;i++)
{
if(b[L[i]]+add[i]>m) continue;//最小值>k
if(b[R[i]]+add[i]<=m) {c+=R[i]-L[i]+1;continue;}//最大值 <= k
int ll=L[i],rr=R[i],ans=0;
while(ll<=rr)
{
int mid=(ll+rr)>>1;
if(b[mid]+add[i]<=m) ans=mid-L[i]+1,ll=mid+1;
else rr=mid-1;
}
c+=ans;
}
}
if(c<k) vL=m+1;
else vR=m-1,ans=m;
}
return ans;
}
signed main()
{
n=rd(),m=rd();
for(int i=1;i<=n;i++) a[i]=b[i]=rd();
for(int i=0;i<=n/T;i++)
{
L[i]=max(1ll,i*T),R[i]=min(n,i*T+T-1);
for(int j=L[i];j<=R[i];j++) bel[j]=i;
sort(b+L[i],b+1+R[i]);
}
while(m--)
{
int op=rd(),l=rd(),r=rd(),k=rd();
if(op==1) printf("%d\n",qkth(l,r,k));
else upd(l,r,k);
}
}
初始化
题意:
给定一序列,每次求区间和或给定 \(x,y,z\),然后令序列下标为 \(y,y+x,y+2x,y+3x,...,y+kx\) 的值加 \(z\)。
\(n\leq 2\times 10^5\)。
500ms,128MB。
乘法相关,根号分治。
考虑一个阈值 \(T\),对于 \(x \geq T\) 的操作,暴力改复杂度为 \(\frac{n}{T}\)。
下面考虑 \(x < T\)。
可以对每一个 \(x\) 分开做。
考虑将序列分为每 \(x\) 个数一段,那么只需要考虑维护第一段,就能代表所有段。
\(y \leq x\) 是非常优美的限制,能很好的放在 \(x\) 个数一段的前提下维护,如下图:
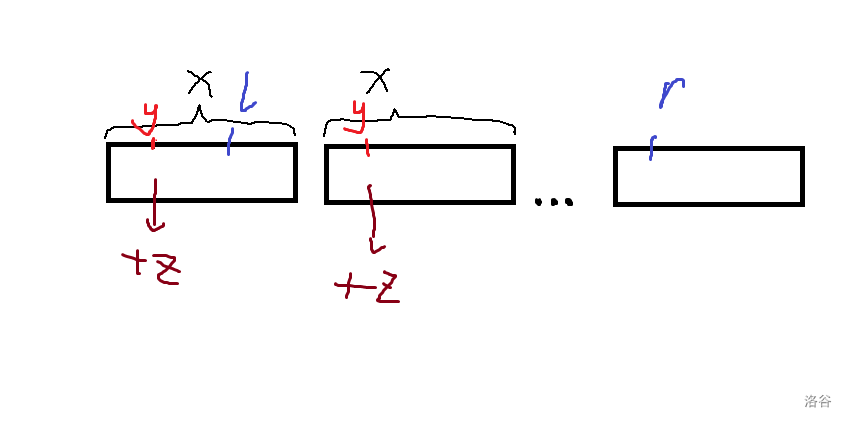
故只需要维护一个后缀和,前缀和数组即可。
卡常技巧:用 c++98,由于 \(\leq T\) 的修改常数极小,这里取 \(T=150\)。
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5,T=150,p=1e9+7;
int n,m,a[N],s[N/T+5],L[N/T+5],R[N/T+5],bel[N],ls[T+5][T+5],rs[T+5][T+5],vis[T];
void inc(int &x,int y) {if((x+=y)>=p) x-=p;}
char buf[1<<15],*p1=buf,*p2=buf;
#define nc() (p1==p2&&(p2=buf+fread(p1=buf,1,1<<15,stdin),p1==p2)?-1:*p1++)
inline int rd()
{
int x=0,f=1;char c=nc();
for(;!isdigit(c);c=nc()) if(c=='-') f=-1;
for(; isdigit(c);c=nc()) x=(x<<3)+(x<<1)+(c^48);
return x*f;
}
void add(int x,int y,int z)
{
if(x>=T) {for(int i=y;i<=n;i+=x) inc(a[i],z),inc(s[bel[i]],z);return;}
vis[x]=1;
for(int i=1;i<=y;i++) inc(rs[x][i],z);//维护后缀
for(int i=y;i<=x;i++) inc(ls[x][i],z);//维护前缀
}
int qsum(int l,int r)
{
int bl=bel[l],br=bel[r],ans=0;
if(bl==br) for(int i=l;i<=r;i++) inc(ans,a[i]);
else
{
for(int i=l;i<=R[bl];i++) inc(ans,a[i]);
for(int i=L[br];i<=r;i++) inc(ans,a[i]);
for(int i=bl+1;i<br;i++) inc(ans,s[i]);
}
for(int i=1;i<T;i++)
{
if(!vis[i]) continue;
int pl=(l-1)%i+1,pr=(r-1)%i+1,kl=(l-1)/i,kr=(r-1)/i;
if(kl==kr) inc(ans,(ls[i][pr]-ls[i][pl-1]+p)%p);
else inc(ans,(1ll*(kr-kl-1)*ls[i][i]+ls[i][pr]+rs[i][pl])%p);
}
return ans;
}
int main()
{
n=rd(),m=rd();
for(int i=1;i<=n;i++) a[i]=rd();
for(int i=0;i<=n/T;i++)
{
L[i]=max(1,i*T),R[i]=min(n,i*T+T-1);
for(int j=L[i];j<=R[i];j++) inc(s[i],a[j]);
for(int j=L[i];j<=R[i];j++) bel[j]=i;
}
for(int i=1;i<=m;i++)
{
int op=rd(),x=rd(),y=rd(),z;
if(op==1) z=rd(),add(x,y,z);
else printf("%d\n",qsum(x,y));
}
}