Prufer 序列 - 无根树的序列化

定义

一种将带标号的树用一个唯一的整数序列表示的方法。
Prufer 序列可以把一颗带标号的 \(n\) 个节点的树序列化为一个长度为 \(n - 2\) 的唯一的序列。
也就相当于完全图的生成树与数列之间的双射。

构造方式

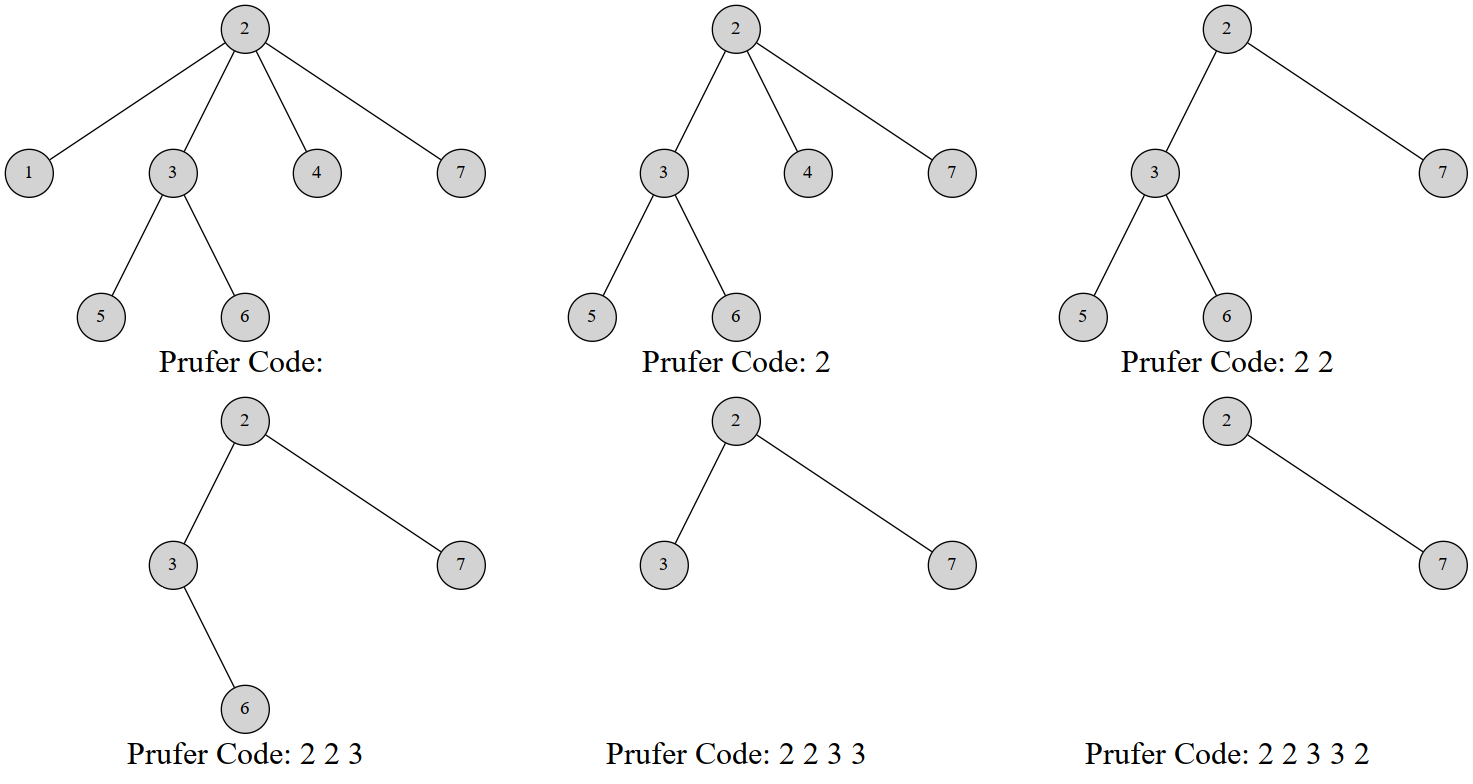
每次选择一个编号最小的叶节点并删掉它，然后在序列中记录下它连接到的那个节点。
重复 \(n - 2\) 次如上操作，此时树上只剩 \(2\) 个节点，算法结束。
如果使用优先队列来构造，时间复杂度显然是 \(O(n\log n)\)。
可以使用指针来构造，将时间复杂度降低至 \(O(n)\)。
首先找到编号最小的，度数为 \(1\) 的叶子节点，指针 \(p\) 指向它，将它删除。
如果删除了这个节点后，它的父亲节点的编号比它小并且父亲节点的度数也变成了 \(1\)，那么此时这个节点一定是编号最小的叶子节点，删除它即可，同时不断往上删除，注意在这个过程中 \(p\) 并不进行移动。
否则的话，继续让 \(p\) 自增，找到下一个编号最小的叶子节点即可。
每条边在删度数的时候最多被访问一次，而指针最多遍历每个结点一次，因此复杂度是 \(O(n)\) 的。

性质

Prufer 序列具有以下性质：

• 构造完 Prufer 序列后剩下的两个节点其中一个是编号最大的点 \(n\)。
• 每个节点出现的次数是度数减一。
• 没有出现在 Prufer 序列里的节点的就是叶子节点。

树的还原

通过 Prufer 序列还原树的方法和构造它的方法差不多。
Prufer 序列告诉了我们每个节点的度数，我们可以找到编号最小的度数为 \(1\) 的节点，根据构造方法来看，它一定和 Prufer 序列的第一个元素相连接。从这里就大概和 Prufer 序列的构造方法几乎一样了。

Cayley 公式

完全图 \(K_n\) 有 \(n^{n - 2}\) 棵生成树。
任意一个长度为 \(n - 2\) 的值域 \([1, n]\) 的整数序列都可以通过 Prufer 序列双射对应一个生成树，于是方案数就是 \(n^{n - 2}\)。

模板题：

• Luogu P6086 Prufer 序列

#define int ll

int n, m;
const int MAXN = 5e6 + 5;
int fa[MAXN], prufer[MAXN], deg[MAXN];

void solve_prufer() {
	rep (i, 1, n - 1) cin >> fa[i], deg[fa[i]]++;
	int pos = 1;
	rep (i, 1, n - 2) {
		while (deg[pos]) pos++;
		prufer[i] = fa[pos];
		while (i <= n - 2 && !--deg[prufer[i]] && prufer[i] < pos)
			prufer[i + 1] = fa[prufer[i]], i++;
		pos++;
	}
	int ans = 0;
	rep (i, 1, n - 2) ans ^= i * prufer[i];
	cout << ans;
}

void solve_father() {
	rep (i, 1, n - 2) cin >> prufer[i], deg[prufer[i]]++;
	prufer[n - 1] = n;
	int pos = 1;
	rep (i, 1, n - 1) {
		while (deg[pos]) pos++;
		fa[pos] = prufer[i];
		while (i <= n - 1 && !--deg[prufer[i]] && prufer[i] < pos)
			fa[prufer[i]] = prufer[i + 1], i++;
		pos++;
	}
	int ans = 0;
	rep (i, 1, n - 1) ans ^= i * fa[i];
	cout << ans;
}