CF1864D Matrix Cascade

思路

第一时间想到的是暴力，因为同一行的互不影响，所以第一行的 \(1\) 一定都需要操作，然后把后续的状态更新，再操作第二行的所有的 \(1\)，但是很可惜是 \(O(n^4)\) 的复杂度，必然会 TLE。

所以思考其他的办法，考虑到可以统计有多少操作更改了这个位置的状态，所以可以使用一个类似前缀和的方法。

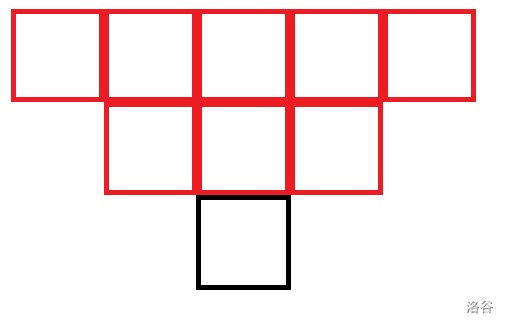
如上图，可以发现黑色方框的状态会被红色方框的操作影响。

所以想办法统计红色方框进行的操作总数。

令 \(b_{i,j}\) 表示格子 \((i,j)\) 是否做过操作， \(c_{i,j}\) 表示所有会影响格子 \((i,j)\) 的状态的操作总数，包括本格子的操作。

再简单画一个图：

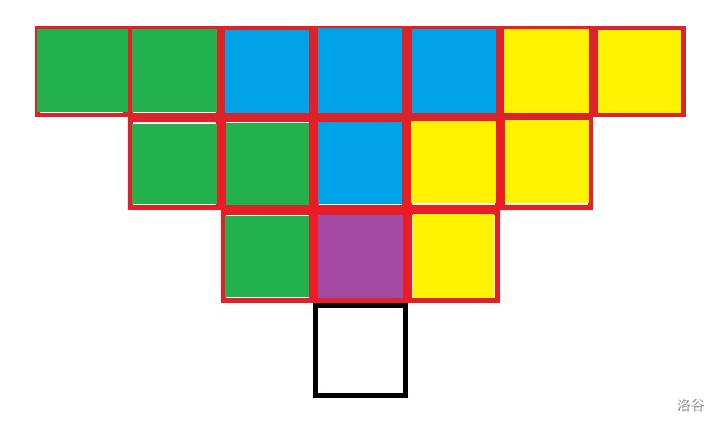
绿色为 \(c_{i-1,j-1}\) 单独涉及的区域，黄色为 \(c_{i-1,j+1}\) 单独涉及的区域，蓝色为 \(c_{i-1,j-1}\) 和 \(c_{i-1,j+1}\) 共同涉及的区域。

所以可以推断出公式为 \(c_{i,j}=c_{i-1,j-1}+c_{i-1,j+1}-c_{i-2,j}+b_{i-1,j}\)。

然后再判断经过这么多次操作后，这个格子的状态，再判断是否需要操作，再更改 \(c_{i,j}\) 和 \(b_{i,j}\)。

然后发现样例都不对，在调试后发现，是当 \(j=1\) 或者 \(j=m\) 时发生了错误，所以只需要特判，这种情况更加简单公式为 \(c_{i,j}=c_{i-1,j+1}+b_{i-1,j}\) 或者 \(c_{i,j}=c_{i-1,j-1}+b_{i-1,j}\)。

AC code

#include<bits/stdc++.h>
using namespace std;
int T,n,a[3005][3005],b[3005][3005],c[3005][3005],ans;
char ch[3005];
int main()
{
	scanf("%d",&T);
	while(T--)
	{
		scanf("%d",&n),ans=0;
		for(int i=1;i<=n;++i)
		{
			scanf("%s",ch+1);
			for(int j=1;j<=n;++j)
			{
				b[i][j]=0,a[i][j]=ch[j]-'0';
			}
		}
		for(int i=1;i<=n;++i)
		{
			for(int j=1;j<=n;++j)
			{
				if(j==1) c[i][j]=c[i-1][j+1]+b[i-1][j];
				else if(j==n) c[i][j]=c[i-1][j-1]+b[i-1][j];
				else c[i][j]=c[i-1][j-1]+c[i-1][j+1]-((i>=2)?c[i-2][j]:0)+b[i-1][j];
				if((c[i][j]%2)^a[i][j]) ++c[i][j],++ans,b[i][j]=1;
			}
		}
		printf("%d\n",ans);
	}
	return 0;
}