前 \(10\) 项为:\(1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862\)
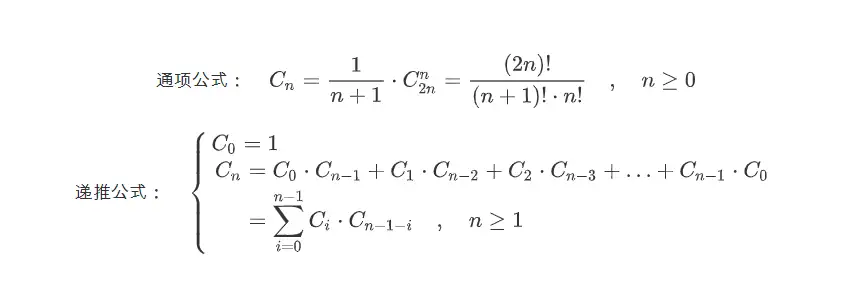
递推公式
\(tip:\) 在 \(n=17\) 时 \(Catalan\) 数就会超过 \(int\) 范围。
\[C_1=1 \]\[C_n=C_{n-1}\frac{4*n-2}{n+1} \]出栈问题
一个栈的入栈顺序为 \(1,2,3,\ldots ,n\) 时,出栈顺序有多少种?
栈中每个元素需要经历入栈出栈,所以会有 \(2n\) 个操作,记入栈为 \(+1\) ,出栈为 \(-1\) ,那么每个合法操作顺序每个前缀和必须 \(\ge0\) 。如果直接求显然不方便,那么正难则反。如果当前 \(n\) 非法,那么需要在所有的 \(C_{2n}^{n}\) 情况中,去掉 \(C_{2n}^{n+1}\) 个非法序列(因为非法序列相当于在 \(n+1\) 个位置放置 \(-1\) ,在 \(n-1\) 个位置放置 \(+1\) )。\(C_{2n}^{n}-C_{2n}^{n+1}=\frac{C_{2n}^{n}}{n+1}\) 此时就得到了 \(Catalan\) 数。
括号问题
\(n\) 对括号能构成多少种合法序列?
很显然与出栈问题相同,答案就是 \(Catalan\) 数。
满二叉树问题
\(n+1\) 个节点可以构成多少种满二叉树?
对于每个节点要么子节点为空,要么同时存在两个节点,如果把左儿子看作 \(+1\) , 右儿子看作 \(-1\) ,那么又与出栈问题相同。
标签:出栈,Catalan,二叉树,序列,2n,节点 From: https://www.cnblogs.com/edgrass/p/17662918.html