去 ZR 的时候接触到的,然后来填坑。
参考资料:
应用
李超线段树最经典的应用就是维护一个二维平面直角坐标系,支持动态插入线段或者直线,询问与直线 \(x = x_0\) 相交的已插入线段中交点 \(y\) 的最大/最小值。也就是当 \(x=x_0\) 时,求 \(\max\{k_ix+b_i\}\) 或者 \(\min\{k_ix+b_i\}\)。这两种情况没有什么本质上的区别,随便改一些地方就能从一种情况转化成另一种了。
算法流程
我们首先从暴力考虑,最朴素的方法就是暴力 \(O(n)\) 求出函数值。考虑优化,这里我们采用的优化方法是减少集合大小,排除不可能成为最优解的,从而降低复杂度。
首先我们要知道李超线段树的核心,李超线段树的核心是维护当前节点维护的区间的中点处最高的线段,我们可以称之为“最优势线段”。那么询问的时候,我们可以对包含横坐标 \(x\) 的区间上的“最优势线段”计算答案,然后取个 \(\max\) 即可,这样可以看出是 \(O(\log n)\) 的。
可以看出,我们相当于维护一个记录当前区间最高线段的,不下传标记的线段树,这其实就是标记永久化的思想。
然后我们再考虑如何插入一个新的线段。我们会用到斜率和新旧线段在区间中点上的取值来进行更新,这需要分类讨论一下,我们设 \(f(x)\) 表示一个线段在 \(x\) 处的取值。
-
(1) 当前区间没有线段,那我们直接将新线段放入当前区间即可。
-
(2) 当前区间有最优势线段,且新线段的斜率大于旧线段的斜率,这又分成两种情况考虑。
\(\circ\) 如果 \(f_{\text{old}}(mid) > f_{\text{new}}(mid)\),那么新线段在 \([l,mid]\) 部分的取值一定没有旧线段优,但是新线段在 \([mid+1,r]\) 可能更优,所以我们将新线段下放到 \([mid+1,r]\) 来递归更新答案。如图
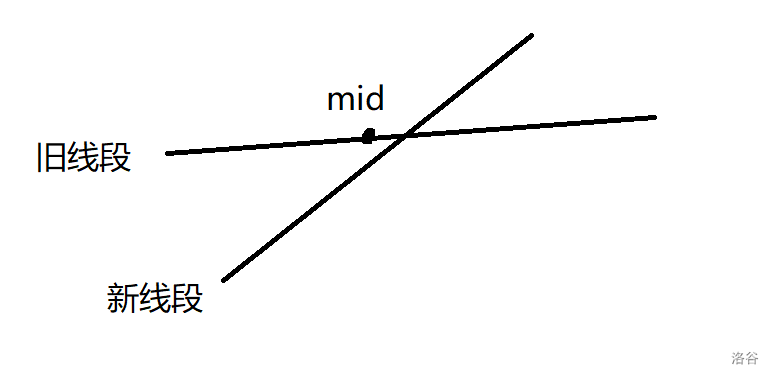
\(\circ\) 如果 \(f_{\text{old}}(mid) < f_{\text{new}}(mid)\),那么旧线段在 \([mid+1,r]\) 部分的取值一定没有新线段优,但是旧线段在 \([l,mid]\) 可能更优,我们将新线段在当前节点替换旧线段,然后将旧线段下放到 \([l,mid]\) 来递归更新答案。如图
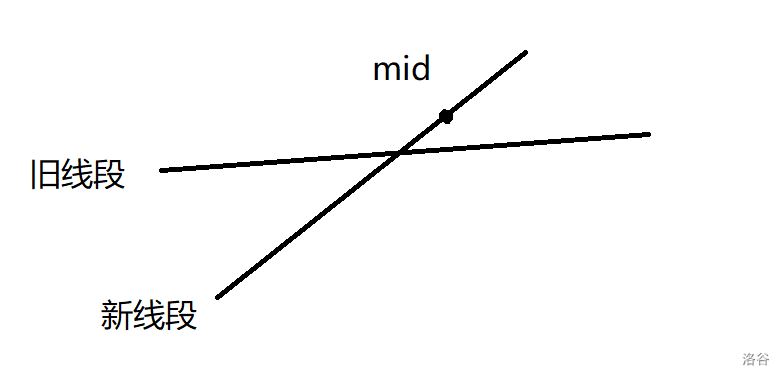
-
(3) 当前区间有最优势线段,且新线段的斜率小于旧线段的斜率,这又分成两种情况考虑。
\(\circ\) 如果 \(f_{\text{old}}(mid) > f_{\text{new}}(mid)\),那么新线段在 \([mid+1,r]\) 部分的取值一定没有旧线段优,但是新线段在 \([l,mid]\) 可能更优,所以我们将新线段下放到 \([l,mid]\) 来递归更新答案。如图
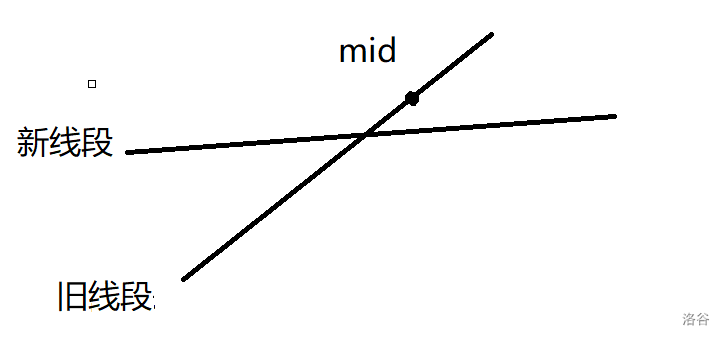
\(\circ\) 如果 \(f_{\text{old}}(mid) < f_{\text{new}}(mid)\),那么旧线段在 \([l,mid]\) 部分的取值一定没有新线段优,但是旧线段在 \([mid+1,r]\) 可能更优,我们将新线段在当前节点替换旧线段,然后将旧线段下放到 \([mid+1,r]\) 来递归更新答案。如图
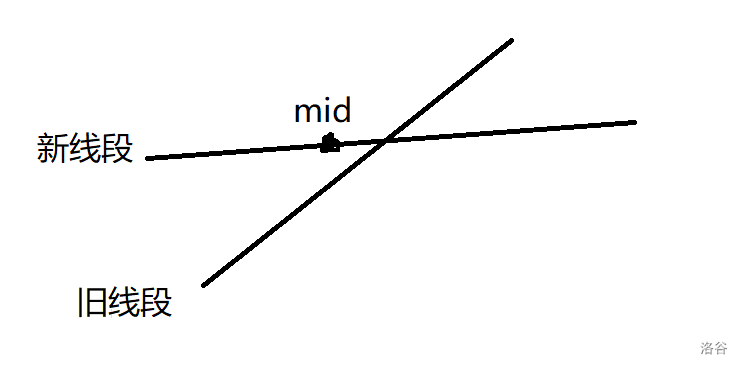
-
(4) 如果当前区间有最优势线段,且新旧线段斜率相同,此时比较截距 \(b\),截距大的直接替换截距小的就行。
我们通过上述过程看出,首先我们要判断这个线段覆盖的范围,然后再更新这个范围内的标记,这样就是 \(O(\log^2 n)\) 的,如果是直线全局修改,那我们就省去了第一个步骤,所以就是 \(O(\log n)\) 的。
代码
给出关键的修改和查询。
il double calc(int id,int x) { return k[id] * x + b[id]; }
il int cmp(double a,double b)
{
if(a - b > eps) return 1;
if(a - b < -eps) return -1;
return 0;
}
il void Update(int p,int l,int r,int y)
{
if(l == r)//单点了直接比较然后返回
{
if(calc(tree[p],l) < calc(y,l)) tree[p] = y;
return ;
}
if(!tree[p]) { tree[p] = y; return ; }//空的,直接插入
int mid = (l+r) >> 1 , x = tree[p];
if(k[x] > k[y])//新线段斜率小于旧线段
{
if(cmp(calc(x,mid),calc(y,mid)) == 1) Update(lc,l,mid,y);
else Update(rc,mid+1,r,tree[p]) , tree[p] = y;
}
else if(k[x] < k[y])//新线段斜率大于旧线段
{
if(cmp(calc(x,mid),calc(y,mid)) == 1) Update(rc,mid+1,r,y);
else Update(lc,l,mid,tree[p]) , tree[p] = y;
}
else if(b[x] < b[y]) tree[p] = y;//斜率相同,比较截距
}
il void Modify(int p,int nl,int nr,int l,int r,int id)
{
if(nl <= l && r <= nr)
{//找覆盖范围
Update(p,l,r,id);
return ;
}
int mid = (l+r) >> 1;
if(nl <= mid) Modify(lc,nl,nr,l,mid,id);
if(nr > mid) Modify(rc,nl,nr,mid+1,r,id);
}
il pdi Max(pdi a,pdi b)
{
int f = cmp(a.first,b.first);
if(f == 1) return a;
if(f == -1) return b;
return a.second < b.second ? a : b;
}
il pdi Query(int p,int l,int r,int pos)
{
pdi res = {calc(tree[p],pos),tree[p]};
if(l == r) return res;
int mid = (l+r) >> 1;
if(pos <= mid) res = Max(res,Query(lc,l,mid,pos));
if(pos > mid) res = Max(res,Query(rc,mid+1,r,pos));
return res;
}
这是维护线段的,维护直线时,我们就不需要 Modify 函数,直接运用 Update 函数即可。
完整代码:P4097(维护线段)、P4254(维护直线)。
标签:return,int,text,线段,tree,mid,李超树 From: https://www.cnblogs.com/bloodstalk/p/17658432.html