出去集训讲了一些有关树状数组的 NB 东西，然后模拟赛考了一个二维树状数组的板子，自己差点没推出来柿子，所以简单写写。

参考博客: 《树状数组进阶》-Alex_wei

树状数组二分

树状数组二分，本质上其实应该是树状数组倍增，它是基于倍增的思想实现的。

算法流程

树状数组二分解决的问题是找到一个分割点 \(q\)，使得 \(\leq q\) 的位置满足某个限制，而 \(>q\) 的位置不满足。并且需要注意的一点是，树状数组二分是要在整个序列上二分，而并非每个序列都可以。

而这个限制，在题中出现最多的就是找到一个位置 \(q\)，使得 \(\leq q\) 的前缀和都要 \(\leq v\)，而 \(>q\) 的位置的前缀和都要 \(>v\)。

因为树状数组中的一个位置 \(i\)，存储的是 \(\displaystyle i-\text{lowbit}(i)+1 \sim i\) 的值，因为这个天然性质，使得我们可以进行这个操作。

我们设当前位置是 \(p\)，前缀和是 \(s\)，我们从大到小枚举 \(1\leq 2^k \leq n\)，尝试将 \(p\) 加上 \(2^k\)，即判断 \(\displaystyle s + \sum_{i=p+1}^{p+2^k}a_i\leq v\) 是否成立。

这样对的原因是我们是从大到小枚举的 \(k\)，所以 \(\text{lowbit}(p+2^k) = 2^k\)，因此这个式子是正确的。那么如果 \(\displaystyle s + \sum_{i=p+1}^{p+2^k}a_i\leq v\) 成立，我们就令 \(\displaystyle p\leftarrow p+2^k,s = s+\sum_{i=p+1}^{p+2^k}a_i\)，一直往下找就行了。

因为这个 \(\displaystyle \sum\) 里面的东西刚好就是树状数组维护的，所以我们就可以在 \(O(\log n)\) 的复杂度内解决这个问题，如果单纯的是二分 + 树状数组（注意不是树状数组上二分），那就是 \(O(\log^2 n)\)，显然是不优的。

例题

• P6619 [省选联考 2020 A/B 卷] 冰火战士

参考题解：duyi

撅世好题。

我们挖掘一些性质：

• 1. 注意到一旦双方出战名单确定，无论出战顺序如何，因为双方耗费的能量一定相同，且至少有一方能量耗尽时才能结束，因此答案是两队能量和最小值的两倍。
• 2. 我们设两个函数 \(\displaystyle f_{ice}(k) = \sum_{i\in \text{ice},x_i\leq k}y_i,f_{fire}(k) = \sum_{i\in \text{fire},x_i\ge k}y_i\)，我们观察这两个函数的图像，可以注意到，关于冰战士的价值函数是单调不降的，关于火战士的价值函数是单调不升的，具体就如下图所示（图片来自 here)

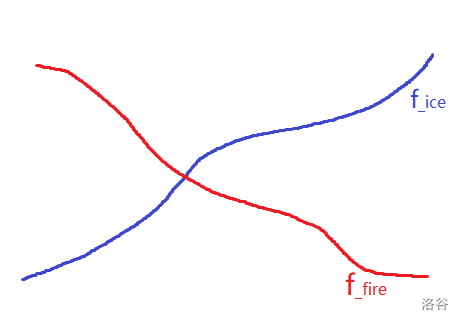
，然后我们要找的就是它们两条线的 \(\min\) 部分里的最大值，也就是下图

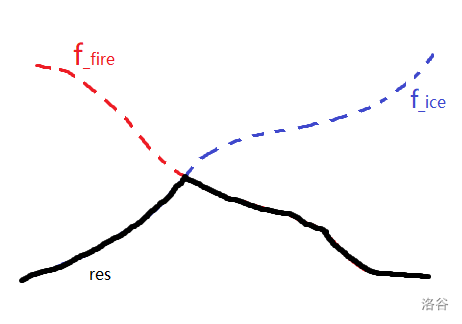
res 部分的那个峰点，但是由于这个函数是定义在整数域上的，所以不连续，所以这样的点可能会有多个，我们就可以拆分成两个问题来做：

• 找出最大的 \(k\)，使得 \(f_{ice}(k) < f_{fire}(k)\)

• 找出最小的 \(k\)，使得 \(f_{ice}(k) \ge f_{fire}(k)\)

然后这两个 \(f\) 我们可以用树状数组维护它们的前缀和，然后在树状数组上二分解决就行了。因为 \(f_{fire}(k)\) 在 res 部分是一个后缀，我们依然可以维护前缀，然后后缀 \(=\) 总和 - 前缀就行了。

但是有一个问题就是树状数组是求了一个前缀和满足 \(\leq\) 的限制，而第二个问题不太好办，怎么解决呢？

具体的，我们先解决第一个问题，找到的位置是 \(p\)，然后我们在 \(p+1\) 的位置上解决问题二，如果第一个问题值更大，那么就按问题 \(1\) 输出；否则，我们利用求出来的问题 \(2\) 的值再树状数组二分一次，这样就能保证找到的位置在最前面了。综上，我们最多只需要 \(2\) 次树状数组二分，因为树状数组常数很小，并且理论复杂度是 \(O(n\log n)\)，所以可以通过 \(2\text{e}6\)。

code:

#include<bits/stdc++.h>
//#define int long long
#define ll long long
#define next nxt
#define re register
#define il inline
#define lowbit(x) x&(-x)
const int N = 2e6 + 5;
using namespace std;
int max(int x,int y){return x > y ? x : y;}
int min(int x,int y){return x < y ? x : y;}

int n,m,cnt,sumfire;
int b[N];
struct node{
	int op,type;
	int t,v;
}a[N];
struct Node{
	int c[N];
	il void add(int x,int k) { for(;x<=n;x+=lowbit(x)) c[x] += k; }
}treeice,treefire;

il int read()
{
	int f=0,s=0;
	char ch=getchar();
	for(;!isdigit(ch);ch=getchar()) f |= (ch=='-');
	for(; isdigit(ch);ch=getchar()) s = (s<<1) + (s<<3) + (ch^48);
	return f ? -s : s;
}

il int Query(int x)
{
	if(x < 1 || x > m) return 0;
	int ans1 = 0 , ans2 = sumfire;
	for(;x;x-=lowbit(x)) ans1 += treeice.c[x] , ans2 -= treefire.c[x];
	return min(ans1,ans2);
}

signed main()
{
	n = read();
	for(re int i=1;i<=n;i++)
	{
		a[i].op = read();
		if(a[i].op == 1)
		{
			a[i].type = read() , a[i].t = read() , a[i].v = read();
			b[++cnt] = a[i].t;
		}
		else
		{
			int k = read(); a[i] = a[k];
			a[i].op = 2 , a[i].v = -a[i].v;//删去一个就相当于贡献为负
		}
	}
	sort(b+1,b+cnt+1);
	m = unique(b+1,b+cnt+1) - b - 1;
	for(re int i=1;i<=n;i++) a[i].t = lower_bound(b+1,b+m+1,a[i].t) - b;
	for(re int i=1;i<=n;i++)
	{
		if(!a[i].type) treeice.add(a[i].t,a[i].v);
		else treefire.add(a[i].t+1,a[i].v) , sumfire += a[i].v;//你要求的是从该位置起始的一段后缀，而树状数组查询前缀和会把自己算进来，如果在a[i].t位置上加
		int I = 0 , F = 0 , x = 0;//就会导致这个位置本不应该被删去却被删了，所以我们在 a[i].t+1 的位置上加数
		for(re int j=21;j>=0;j--)
		{
			int nx = x | (1<<j);
			if(nx <= m)
			{
				int nI = I + treeice.c[nx] , nF = F + treefire.c[nx];
				if(nI <= sumfire - nF) x = nx , I = nI , F = nF;
			}
		}//树状数组上二分
		int ans1 = Query(x) , x2 = x + 1 , ans2 = Query(x2);
		if(ans1 <= 0 && ans2 <= 0) puts("Peace");
		else if(ans1 > ans2) cout << b[x] << " " << (ans1<<1) << "\n";
		else//第二次树状数组二分
		{
			int F = 0 , x = 0;
			for(re int j=21;j>=0;j--)
			{
				int nx = x | (1<<j);
				if(nx <= m)
				{
					int nF = F + treefire.c[nx];
					if(ans2 <= sumfire - nF) x = nx , F = nF;
				}
			}
			cout << b[x] << " " << ((sumfire-F)<<1) << "\n";
		}
	}
	return 0;
}

二维树状数组

先放一放。