题意
有一个 \(n\times n\) 的方格图,坐标编号类似平面直角坐标系,左下角为 \((1, 1)\)。
这个方格图被分成了 \(n\) 层,左下角 \((1, 1)\) 为第一层,随后每层都向外拓展一圈,如下图就是 \(n=5\) 的时候的情况:
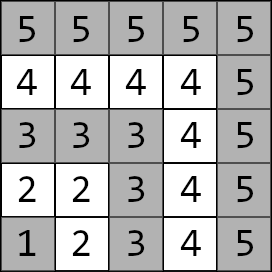
层与层之间有墙隔开,但每层都有两个门,分别分布在该层顶部和右侧,门是双向的。
现在给出这些门的坐标,有 \(m\) 次询问,每次给定两个坐标 \((x_1, y_1)\) 和 \((x_2,y_2)\),请你回答两点之间的最短路。
题解
分块做法。
首先读题可以发现门是一定要走的,考虑利用 \(\text{DP}\) 预处理出门与门之间的最短距离,设 \(f_{i,j,0/1,0/1}\) 表示从顶部 / 右侧门到达第 \(i\) 层后到通过顶部 / 右侧门到达第 \(j\) 层的最优路径长度。该式的转移是平凡的。
考虑利用分块优化,对于每个块块内处理出两两点对之间的 \(f\) 值,对于块块之间按也处理出类似的 \(\text{DP}\) 值。
需要平衡复杂度,设块长为 \(B\),那么每个块内有 \({B}\) 个元素,即 \({B}^2\) 个点对关系。因为共有 \(\dfrac{n}{B}\) 个块,所以这部分的复杂度为 \(\mathcal{O}\left(nB\right)\)。共有 \(\dfrac{n}{B}\) 个块,即 \(\left(\dfrac{n}{B}\right)^2\) 个点对,复杂度为 \(\mathcal{O}\left(\left(\dfrac{n}{B}\right)^2\right)\)。
令 \(nB = \left(\dfrac{n}{B}\right)^2\),得 \(B = n^{\frac{1}{3}}\),总复杂度为 \(\mathcal{O}(n^{\frac{4}{3}})\),可以通过本题。
Code
出于篇幅考虑,代码另行发布。
标签:CF1681E,Labyrinth,题解,复杂度,right,dfrac,mathcal,left From: https://www.cnblogs.com/User-Unauthorized/p/solution-CF1681E.html