[CEOI2011] Matching 题解
题外话:
看了其他人题解后作为初学 $kmp$ 的我非常蒙,因为对这个算法的核心掌握不太好,不知道怎么维护动态的序列,因此写下此题解共享经验,建议只会打模板的看看。
参考资料:
https://www.cnblogs.com/fusiwei/p/11944975.html
思路引导:
看到数据范围,又和真实值没有太大关系,立即离散化,不再赘述。
首先,我们能看出这是一个类似匹配的问题,即对于任意一个和 p 相同长度的 a 的子串,要求其排名序列和 p 一毛子一样。那么这样的话,一般情况下我直接在 a 前面接上 p 然后跑一遍模板 $kmp$ 就好了。
但是出现了意外,原因是:我的主串 a 的子串和模式串 p 不一定一模一样(大多数不一样),但是仍应该匹配。
所以我们考虑如何让 a 的某个子串和 p 一模一样达成匹配。
如果您看了前面的题解,那么可以知道一种方式:将 a 的子串和 p 的第 i 位表示为 i 位置之前比他大的数有多少个。很显然这样就能达成匹配。例子的话,其他题解给出了,这里不再重复。并且个人认为,树状数组维护这个东西是显而易见的。
然后就是困扰我许久的问题:用 $kmp$ 算法怎么处理动态的数组呢?(为什么是动态?因为我们发现对于同一个位置 i,考虑的子串不同,那么他对应的排名也不同,相应地,他前面比他大的数字个数也不同。
首先,很明显的是,我们模式串 p 肯定不会改变吧。
其次,通过上文的参考资料可以得知, nxt 数组只和模式串 p 有关系(因为跳 nxt 数组时,只是模式串在跳)。于是我们可以先求出这个数组。
那么显而易见的,我只要维护好在跳 nxt 数组时的主串末尾变化即可。
不懂?我们用下图来辅助一下。
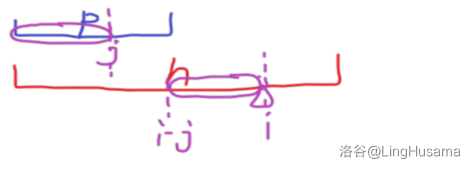
假设我们上一次匹配到了 j 位置,正在匹配 i 位置。
首先我们要尝试一下 $h_i$ 这里能否和 $P_{j+1}$ 这个位置达成匹配,准确来说,是看他们的位置上的排名是否相等,很显然,如果相等的话,i 位置的答案就是 $j+1$。
要是无法达成匹配,我们就要跳 $p_j$ 的 nxt 数组,尝试能否达成匹配。但是显然,我在跳 nxt 数组时,相应的后缀的长度会短,我应该在主串中删除不在变短的后缀中的数字以免影响排名,而这些数字所在的区间正是 $[i-j,i-nxt[j]-1]$ ,我们用树状数组也可以强制删除噻。
最后达成匹配,看他的长度是否和 p 的长度相等,相等的话就说明完全匹配上了。但此时你的指针位置在这个合法区间的末尾,因此答案应该加入 $i-n+1$。
代码:
个人感觉思路很重要,建议理解后自己写。
#include<bits/stdc++.h>
#define int long long
const int mod=1e9+7;
using namespace std;
int p[1000006];
int h[1000006];
int c[1000006];
int lsh[1000006];
int len[1000006];
int cnt[1000006];//可以看作是数->排名的一种映射,只和p有关
int nxt[1000006];
vector<int>ans;
int lowbit(int x){
return x&(-x);
}
void add(int pos,int val){
for(int i=pos;i<=1000000;i+=lowbit(i)){
c[i]+=val;
}
}
int query(int pos){
int ret=0;
for(int i=pos;i>=1;i-=lowbit(i)){
ret+=c[i];
}
return ret;
}
signed main(){
ios::sync_with_stdio(false);
int n,m;
cin >> n >> m;
for(int i=1;i<=n;i++){
int k;
cin >> k;
p[k]=i;
}
for(int i=1;i<=m;i++){
cin >> h[i];
lsh[i] = h[i];
}
sort(lsh+1,lsh+1+m);
for(int i=1;i<=m;i++){
h[i]=lower_bound(lsh+1,lsh+1+m,h[i])-lsh;
}
//离散化结束,开始尝试kmp
cnt[n+1] = -0x7fffffff;
for(int i=1;i<=n;i++) {
cnt[i] =query(p[i]);
add(p[i], 1);
}//最前面的串的排位
for(int i = 1; i <= m; i++) {
c[i] = 0;
}//清空
int j=0;
for (int i=2;i<=n;i++) {
while (j&&query(p[i])!=cnt[j + 1]) {
for(int k=i-j;k<=i-nxt[j]-1;k++){
add(p[k], -1);
}
j=nxt[j];
}
if (query(p[i])==cnt[j+1]) {
j++;
add(p[i], 1);
}
nxt[i] = j;
}
// for(int i=1;i<=n+1;i++){
// cout<<cnt[i]<<" ";
// }
// cout<<endl;
for (int i=1;i<=m;i++) {
c[i]=0;
}
j=0;
for (int i=1;i<=m;i++) {
while (j && query(h[i])!=cnt[j + 1]) {
for (int k=i-j;k<=i-nxt[j]-1; k++){
add(h[k],-1);
}
j = nxt[j];
}
if (query(h[i])==cnt[j+1]) {
j++;
add(h[i], 1);
}
if (j==n){
ans.push_back(i-n+1);
}
}
printf("%d\n",ans.size());
for (int i=0;i <ans.size(); i++) {
printf("%d ",ans[i]);
}
}