自我总结
基础规则
- 每行每列不能有重复数字
- 数独有九个小正方形,每个小正方形有 9 个数字,小正方形内也不能有重复数字
概念:
- 行:数独中的一行,记为r。例如第一行为r1
- 列:数独中的一列,记为c。例如第二列记为c2
- 宫:标准数独由9个九宫格组成,一个九宫格叫宫,记为b。从左至右,从上自下依次排序。例如第一宫记为b1
- 区:行、列、宫的统称。
定理
- 定理1:区内无重复数字
- 推论1:当一个区内只剩下1个空没填时,应填入区内未出现的数字
-
基础解法
-
解法 1:找空法
- 原理:行列小正方形中不能出现重复数字,因此若空较少时容易根据其它行列确定剩下的数字
- 剩 1 空:行、列、小正方形中哪个没填就填哪个
- 剩 2 空:寻找是否有行、列可排除剩下两个数字中的一个
- 剩 3 空:寻找是否有 2 行、2 列可排除,例如:

- 剩 4 空:寻找交叉的一行一列,将 3x3 的小正方形中 3 个空占去
-
解法 2:交叉比对
-
2 行 2 竖:
- 发现 1:某个数字有 2 行、2 竖
- 发现 2:2 行和 2 竖都相交于同一个小正方形
- 发现 3:小正方形里没有该数字
- 结论:马上确定剩下数字为该数字,附上例图:

-
进阶版:2 行 1 竖或 2 竖 1 行
-
-
根本原理:每行只有一个数字,因此在同一水平或竖线上的小正方形内必有三个重复数字。
常见范式:
3 空一行切 2:
2 行余 1 空
二线风筝
本文由 简悦 SimpRead 转码, 原文地址 www.zhihu.com
2-String-Kite,江湖人称二线风筝。

把重点放到候选数 4 上面,留意 R2 和 C3,他们都只有两个单元格包含候选数 4,同时还有两个单元格共块(B1),这个时候,4 无外乎两种可能,r2c2-r7c3 或者 r2c4-r3c3,无论哪种情况,r7c4(上图中画圈圈的那个单元格)都能被 4“看见”,所以 4 不能位于该单元格中,这个时候要将 4 从 r7c4 中移除,如法炮制,5 也是一样的情况。
这个时候画圈圈的单元格中只剩下 2,当然就必须 2 了。剩下的就太简单了,我就不啰嗦了,直接在丢出结果是这样:

PS:如果同时把注意力集中在 4 和 5 上面,这个时候的技巧叫做 Remote Pair,同样能得到相同的结论,但是二线风筝这一技巧还是比较适合初学者,也容易理解一些,毕竟同时只关注一个候选数。
JohnT28
题目如下:

本题解法很多,现提供一种简便的方法:
假设第八行第五列为 5,则第八行第二列不是 5,这样第七行第三列只能为 5,第三行第三列不是 5,第三行第五列便是 5,这与原假设矛盾。因此,第八行第五列不是 5,而是 4。后面难度不大,顺势推下去就行。
上述的技巧称为 X - 链,是强迫链的特殊形式。本题的 X 是 5,围绕是 5 非 5 展开推理,很有特色。
基础入门
本文由 简悦 SimpRead 转码, 原文地址 zhuanlan.zhihu.com
不了解数独的人,请先看我第一篇文章
现在你应该知道数独的基本规则,以及行、列和宫
避免你没看前面那篇文章,我解释一下我用到的坐标体系
R 代表行,C 代表列,B 代表宫
R1C1 指第一行第一列那个格子
R23C1 指第一列的第二行和第三行 2 个格子
R1C23 指第一行的第二列和第三列 2 个格子
B1 代表第一宫
本文只是数独的基础技巧和快速入门,如果都学会还想继续深入,请等待我的后续文章
把这篇文章的技巧都能用的出神入化以后,你玩数独已经很厉害了
好了,说正题。
做数独第一个要用到的技巧和思路是什么呢?
答案一定是 「排除法」
什么是排除?
根据数独规则,如果某格内出现了一个数字,与该格同行、同列同宫的位置不能再出现相同的数字。这种排斥同行、同列、同宫其它格内出现相同数字的思路就是排除。见下图:
图中出现的已知数 5,可以排除掉同行、同列和同宫中其他格子内填 5 的可能,即打叉的格子不能再填 5 了,否则和数独的规则矛盾了。

排除法怎么用?
排除法主要分为:1 宫内排除法、2 行列排除法、3 区块排除法。
宫内排除法
针对某宫进行排除,找到只有一个位置可以填某数。
见下图
观察数字 2
B1 和 B3 的 2 让 B2 的 R12 都不能填 2,那么 2 只能在 R3C6
B3 和 B4 的 2 让 B6 的 C8 和 R6 都不能填 2,那么 2 只能在 R5C9

行列排除法
针对某行或某列进行排除,找到该行或该列只有一个位置可以填某数。
观察 R5,B6 的 2 让 R5 在 B6 的 3 列都没法填入 2,所以 2 只能在 R5C6

再看一个例子
还是看 R5,C268 的 2 都因为这些列已经有 2 无法填入,那么 2 只能在 R5C9

区块排除法
某一个数字在一个宫里面,只出现在某一行或者某一列,那么在这一行或者列的其他宫内就不能出现了。
利用排除形成区块,再利用该区块作为排除其他位置的条件进行推理填数。
r5的4使B6的4只可能在 R46C9 这两个格子中,说明 C9 的 4 也就一定在这两个格子里面,B9 的 4 不能出现在 C9,只剩下一个位置可以填入,R9C8 就一定是 4

再看一个例子
R4 的 8 让 B4 的 8 只能出现 R6 中,这样的 R6 的 8 一定在 B4 的这三个位置
这样 C8,R4 和 R6 交叉排除,B6 的 8 只能出现在 R5C9

唯余法:也称唯一余数法,指的是某格里只剩下唯一的数字可以填了。
数独中任意一个格子都可以填入 1-9,如果某格的同行、同列和或同宫中已经出现了 8 个不同的数字,那么该格只能填入没出现的第 9 个数字。
这个思路与排除法不同,排除法是利用已知数字填出相同的数字,而唯余法是利用已知数字填出不同的数字。
例子1:

c8余1、2、3、4、5,r5余1、6、7、8、9,两相结合知c8r5必为1
例子2:

r5余1、4、5、6、7、8、9,c6余1、2、3、4、5,B5余1、2、3、6、8、9,结合知r5c6必为1
数对占位法:利用数对占位作为间接条件,再配合其他数字的排除推理的方法。
数对就是两个候选数组成的一对数字
数对占位指的是无法确定的同一组数对只占据2个格子,其它格子不可能出现,只是说这两个格子到底是数对里哪个数字还不清楚。
例子1:
R4 的 24 和 R6 的 24,让 B5 的 24 只能出现在 R5C56,即有数对24,此时B5其它位置必不会出现2或4
且C4 的 3 和 C5 的 3 排除完后,B5 的 3 的位置是 R56C6
R5C6不能填入 3,3 就只能在 R6C6 了

数对最重要的是起一个占位的作用,虽然我不知道 24 在这两格里面的具体位置,但我把这两格占住了,除了 24 其他的都不能填,你填了除 24 外的任何一个数字,24 中就有一个没法填了
数对还有一个作用是做删减,如果有些数对是通过唯一余数法出来的,比如还是 24,那么除掉这两个格子,其他和这两个格子相关的地方都不能是 24
怎么解一个数独
- 找已知数最多的那个数字,用宫内排除法,看看是不是能确定其他 1 的位置,就算不能确定,也先做好笔记
- 做笔记时注意超过 4 个的都值得先做笔记,同时注意区块排除法
- 找相关已知数最多的格子,看看唯余法是不是能够把数字直接填出来,就算填不出来,也请做好笔记,这个时候这个格子基本只有 2-3 个候选数
- 接下来找已知数最多的行,列,宫,比如某一行已经有 6 个数出现了,只剩下 3 个,先看看能不能填入数字,如果填不进也做好笔记
- 找数对,然后再排除
- 重复上面的步骤,如果没解出来,就应该需要把所有格子能够填入的数字都做好笔记了
- 再找一次数对,做一次排除,这个时候大部分的数独就应该能解决了。
- 如果解决不了,说明这个数独的难度超过了这篇文章所说的方法,后续我还会接着写更多的方法。
数对删减法
本文由 简悦 SimpRead 转码, 原文地址 zhuanlan.zhihu.com
在介绍数独入门的时候,已经说过数对了,但我还是要写一篇文章专门讲一下,掌握了数对,大部分的数独已经难不倒你了。
到这,我相信你对于排除法和唯余法都掌握了,如果还没有,再去看下我前面的文章
数对(数组)是什么,有什么用?
我自己的理解是这样的,N 个数字出现在 N 个有关的格子里面,那么和这几个格子有关系的格子里面不能有这些数字。它的主要作用是占位,这几个数字已经被我这几个格子占住了,其他格子不能用了。
好了,还是上图

看上图,B1 里面有两个格子里面有 37,两个格子两个数字,37 这两个数字已经被这两个格子占住了,所以 B1 其他格子里面不能有 37,就是 B1 打叉的地方。
为什么能占住呢?
如果 B1 打叉的格子里面有 37 任意一个数字,那么现在 37 的这两个格子一定有一个没法填数进去,无论外面用了 3 还是用了 7,这两个格子都剩下同一个数字,出现矛盾。
两个格子两个数字还是比较容易看的
来看一下 C8,3 个格子分别是 456,46,56
但这三个格子数字的并集就是 456 三个数字,三个格子三个数字,这三个数字就被占住了,C8 打叉的地方不能有 456 这三个数字
数对(数组)一般最多看到 4 个数字,再多一定有一组少的数对(数组),或者有一个唯一数可以填
我们来看一个实例

大家看出来哪有数对(数组)了么?
我把我看到的放上来

R2 有 49,B2 有 89,无论用那个,B2 里面 R2 的 9 都可以删掉
B8 有 3 个格子都有 168,那么 R8C6 里面的 168 都可以删掉
删完后是这样的

R8 又有 47 数对了,R8 其他位置的 47 都可以删除,这样 B7 就只有一个 4 了,可以接着填数了。
SDC
本文由 简悦 SimpRead 转码, 原文地址 www.zhihu.com
张齐天
Emmmm……
这个题有个技巧叫做 SDC,暂时没有中文名(:з)∠)
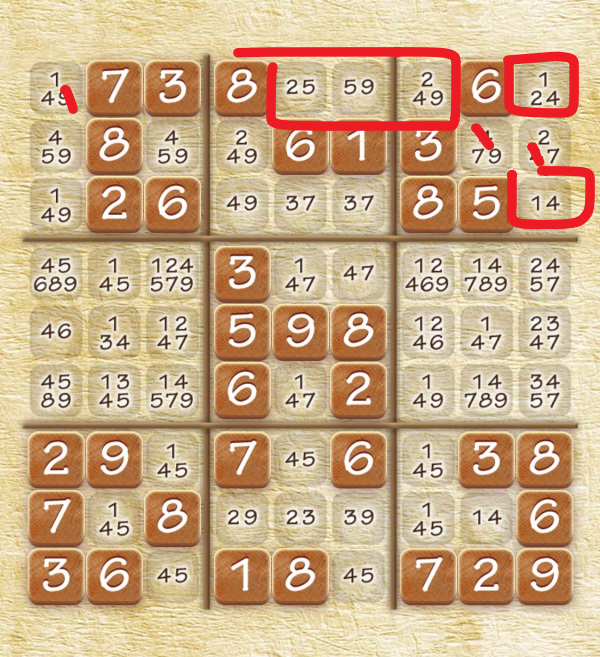
观察框起来的几个单元格,你可以发现,给的数字 1、2、4、5、9 没有一个数字跨区域出现。什么意思呢?框起来的区域里,比如拿 1 来说,1 只在第 1、3 行第 9 格(记作 r13c9,后同)出现,它们都是同一个宫里的。
同理,2、4、5、9 也都满足要求。
试想一下,五个单元格内显然要填入五个数,但恰好这五种不同的数字全部都不会跨区,是否意味着五个数 “完全不重复地” 出现在这五个单元格里,且一个数对应一个格,不多不少呢?
是的,我们确实能得到这个结论,所以,我们就知道,第一行的其余非框内的单元格位置都不能填入 2、5、9,而第 3 个宫里非框内的单元格都不能填入 1 和 4,把它们全删掉。
SDC 全称 Sue de Coq,是个网名,有这个网名的这个人发现了这个技巧,人为了纪念他就把这网名拿来搬过来称呼这个技巧了。
前段时间恢复了一点腱鞘炎写了俩帖子:
Sue de Coq 到底是什么?那么 Sue de Coq 怎么观察呢?
我相信你如果看不懂上面的描述,这篇帖子或多或少都可以给你带来一点思维方式。评论区一直有人说假设,我个人并不是很喜欢这个说法。我承认这个假设的逻辑带入到这个例子里确实行得通(而且并不只是这种技巧可以用假设)。但假设这种思维方式未免有一些暴力,我还是比较喜欢比较接近正常的、可以锻炼逻辑推理思维的一种方式来理解,而假设这个东西确实应该是人人都应该知道的(毕竟你学过数学或多或少就能接触到这个词到底是什么意思),就不属于需要特别学习的思维了。
不过上面的描述我依然不会修改,我希望你能自己理解(哪怕 “跨区域” 这个说法看文字它就是不容易理解,我也希望你自己思考)。
匿名用户
这个题目的难度是 8.3,属于过分难的题目了。必须靠很高级的技巧才能求解。比赛一般也不会出这种题目。
如果你非要推理求解,请下载 Sudoku Explainer,里面可以一步步教你怎么解。
只是要求下一个数字已经要用到 Bidirectional Cycle、 Forcing Chain 这种方法了。。我也不会。
举个例子:
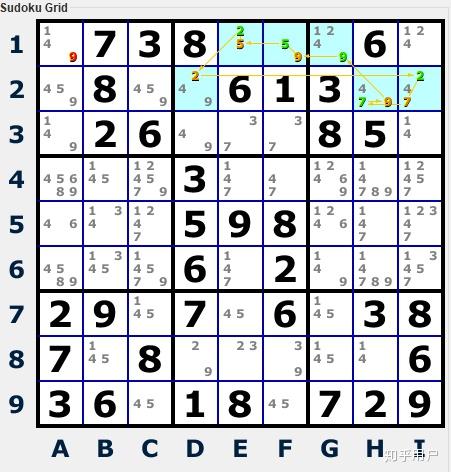
Bidirectional Cycle
The cells E1, D2, I2, H2, G1 and F1 form a bidirectional cycle: there are exactly two ways of placing the values in these cells, forming two different possible configurations. Some values appear in a row, column or block regardless of the chosen configuration. Because one of the two configurations must be correct, other occurances of these values can be removed from these rows, columns or blocks.
The two configurations of the bidirectional cycle are enforced by two complementary, circular chains of implications. The details of each chain are given below.
Cycle details, forward direction (View 1):
(1) If F1 contains the value 5, then E1 cannot contain the value 5 (the value can occur only once in the block)
(2) If E1 does not contain the value 5, then E1 must contain the value 2 (only remaining possible value in the cell)
(3) If E1 contains the value 2, then D2 cannot contain the value 2 (the value can occur only once in the block)
(4) If D2 does not contain the value 2, then I2 must contain the value 2 (only remaining possible position in the row)
(5) If I2 contains the value 2, then I2 cannot contain the value 7 (the cell can contain only one value)
(6) If I2 does not contain the value 7, then H2 must contain the value 7 (only remaining possible position in the block)
(7) If H2 contains the value 7, then H2 cannot contain the value 9 (the cell can contain only one value)
(8) If H2 does not contain the value 9, then G1 must contain the value 9 (only remaining possible position in the block)
(9) If G1 contains the value 9, then F1 cannot contain the value 9 (the value can occur only once in the row)
(10) If F1 does not contain the value 9, then F1 must contain the value 5 (only remaining possible value in the cell)
 爱凡学堂
爱凡学堂
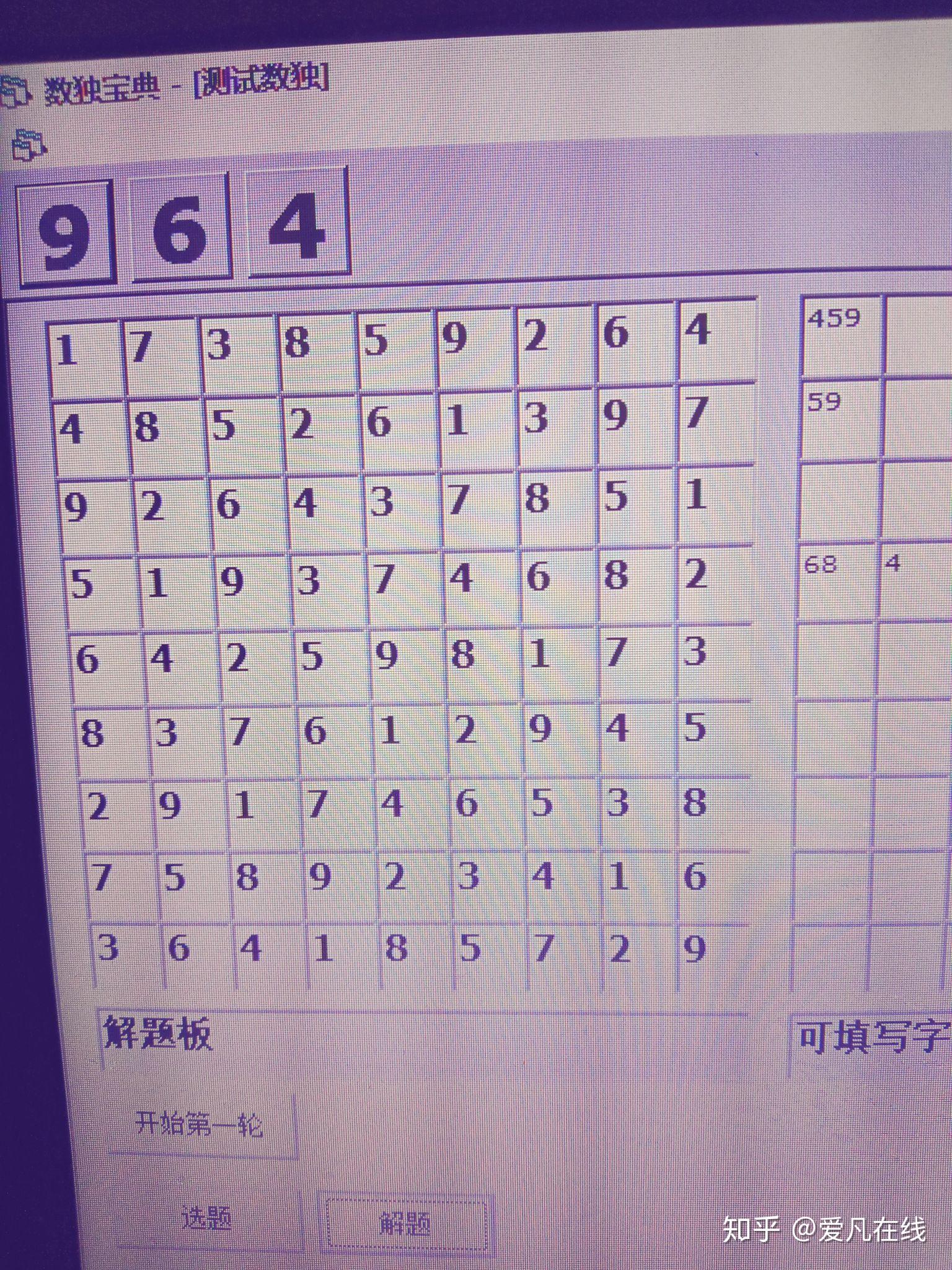
可以跳出人的思维,用程序思维来解。这道题还是有难度的,我的算法要 4 秒才能算出来
大佬合集:
(69 封私信 / 81 条消息) 王西 - 知乎 (zhihu.com)
数组法
本文由 简悦 SimpRead 转码, 原文地址 zhuanlan.zhihu.com
第一节什么是数组?

一、数组的定义
〔一〕数组在中文里面有三个名字:数组、链数和元组。
〔二〕数组是用于储存多个相同类型数据的集合。
1、九宫标准数独的规则:根据 9×9 数独初始盘面上的提示数,通过逻辑推理,将数字 1-9 填入剩余的空格内。使得每行,每列,每个粗线围成的 3x3 小九宫内,均出现数字 1-9 各一次且没有重复的数字出现。
2、根据数独的规则,可以得到:
(1)一个单元格中只能最终填入唯一的一个数字。
A 可以得到这样的推论:两个单元格中需要填入两个数字,三个单元格中需要填入三个数字。
B、总而言之,有多少个单元格,就有多少个数字。
(2)同区中均出现数字 1-9 各一次且没有重复的数字出现。
A、可以得到这样的推论:针对同行的两个单元格,一定要填入两个数字,这两个数字一定是两个不同的数字,不能是相同的数字。
B、同样的道理,针对某列或某宫的两个单元格,一定要填入两个数字,这两个数字一定是两个不同的数字,不能是相同的数字。
C 总而言之,在同区中,有多少个单元格,就有多少个不相同数字。
3、根据数独规则的推论,可以得到:
A 两个单元格中要包含两个不同数字,两格与两数的关系可以称作二数组。二数组,常常被称作数对。
B 同理:
三个单元格中要包含三个不同数字,三格与三数的关系可以称作三数组。
四个单元格中要包含四个不同数字,四格与四数的关系可以称作四数组。
C 总而言之,有多少个单元格,就有多少个不相同数字,N 格与 N 数的关系可以称作 N 数组。
〔三〕数组,这里指同区确定数组,是同一区域下的两个或以上的单元格内,确定只能填入某些数字,并且可以换着填都没毛病的结构。
1、同区,指在同一个区域,具体说就是同行、同列或同宫。
2、确定,是指数字种类的数量和格子的数量是确定的,也就是说,单元格有 n 个同时数字也有 n 种。
〔三〕数组还有复杂的用法
1、数组也可以存在不同区域内。如远程数对。
2、单元格的数量和数字种类的数量也可以是不同的。如待定数组。
二、数组的核心本质
〔一〕格找数填:n 个单元格只能填入 n 种数字
〔二〕数找格填:n 种数字只能放在 n 个单元格里。
三、数组的分类
〔一〕分类的目的是为了解题。
1、解题总的来说有三种方法,直观法、候选数法和试数法。
(1)其中,试数法也叫试错法,先尝试填入数字,然后再填入其他数字,如果出错了,就说明开始填入的数字是错的。然后再换另外一个数字,再进行一番尝试。如果再出错,就再换一个数字尝试。直到找到正确的数字。
(2)其中,重点讲的是直观法和候选数法,这两种方法有技术含量,也可以快速的出数或者删数。
2、直观法(Direct):表示不需要标记任何候选数就可以完成的做题模式。
3、候选数法(Candidate):表示某个单元格的可能填入的情况。一个可能情况就是一个候选数。
4、因此,从直观法和候选数这两个视角来研究分类。
〔二〕从直观法的视角
1、一个单元格中,只能填入一个数字;只能填入在此格所行列宫中都没有出现的数字。
2、针对一行中的两个单元格,只能填入二个数字;只能填入每一格所行列宫中都没有出现的数字。
3、同理,针对一列(宫)中的两个单元格,只能填入二个数字;只能填入每一格所行列宫中都没有出现的数字。
4、同理,针对同区中的 N 个单元格,只能填入 N 个数字;只能填入每一格所行列宫中都没有出现的数字。
5、因此,从余数法的视角,数组是没有分类的。
〔三〕从候选数法的视角
1、候选数有两种标记方法
(1)局部标记(Partial Marked):标记其中某一个或某一些单元格的候选数,用于辅助推理的做题模式。
(2)全部标记(Full Marked):将盘面的所有单元格的所有可能填数情况都标记出来的做题模式。
(3)这里采用全部标记的方式来讲解
2、从候选数法的视角,数对有两种:显性数组和隐性数组。
〔四〕显性数组

实例一
1、从直观法的视角来分析
〔1〕用余数法推算 r7c1 和 r7c7 中应该填入的数字

r7c1 所在的宫 B7 出现的数字:23456
r7c1 所在的行 R7 出现的数字:123459
r7c1 所在的列 C9 出现的数字:15

在宫 B7、行 R7 和列 C9 中没有出现的数字:78
数字 78 就是格 r7c1 的候选数,记作 r7c1(78)

同样的推理,可以得出:r7c7 格的候选数是 78,
记作 r7c7(78)
〔2〕发现显性数对

可以发现:第七行 R7 中,
A7 和 8 两个数字分布在两个单元格 r7c1 和 r7c7 中。
B 有两个数分布在两个单元格中,就称作二数组。
C 两个单元格中的候选数是一样的,都是 78,所以也叫做数对。
D 在同区中,两个单元格中只有两个候选数,就叫做显性数对。
〔3〕通过直观法,想发现数组是不容易的。
2、从候选法的视角来分析
〔1〕全标候选数

利用余数法对全盘标记候选数
〔2〕找到同区的数组
按照宫→行→列的顺序来观察
寻找双值格,就是只有两个候选数的单元格。
寻找同区中的候选数字相同的两个双值格。

很容易就会在第七行 R7 中发现候选数相同的两个双值格 r7c1 和 r7c7。
〔3〕在同单元内其中 n 个单元格内只有 n 种不同的数字,一看就明白,因此称为显性数组。
本例中,两个单元格 r7c1 和 r7c7 中,只有两种不同的数字 7 和 8,因此称为显性数组。由于只有两个候选数,就称作显性二数组,或者叫显性数对。
r7c1 和 r7c7 两个单元格中包含两个数字(78),记作
r7c17(78)。
〔4〕同样的盘面,用直观法观察数组很难发现,但是,用候选数法,则相对更容易发现。
〔五〕隐性数组

实例二
1、从直观法的视角来分析
〔1〕利用排除法推算单元格的候选数。

基础排除法是利用单数对某个区域做排除,这里做一下升级,用两个数字对某个区域做排除。
本例选择 4 和 9 这两个数字对第九列 C9 进行排除。
为了方便理解,可以分别用 4 和 9 对第九列作排除,最后再将结果放在一起。

A、数字 4 对第九列 C9 作排除,得到两个空格。数字 4 如果不再 R2C9 格,就一定在 R9C9 格,记作 R29C1(4)

B、数字 9 对第九列 C9 作排除,得到两个空格。数字 9 如果不再 R2C9 格,就一定在 R9C9 格,记作 R29C1(9)
C、综上所述:数字 4 和 9 都只可以出现在 R2C9 和 R9C9 这两个格中,记作 R29C1(49)。

D、现在利用两个数字作排除。
(a)根据数独规则,每一格必填一个数字,或者说一个数字最终只能填入一个格子。
(b)所以,两个数字最终要填入两个格子。现在利用两个数字作排除,最终也要至少剩下两个空格。
(c)当经过排除之后,只剩下两个空格时,这就构成了数对。
(d)利用画排除线的方法,可以很容易的得到两个空格 R2C9 和 R9C9。因此,对于行来说,数字 4 和 9 只能出现在 R2C9 和 R9C9 中,记作 R29C9(49)
E、先说一下结论,R29C9(49)也称作隐性数组。
2、从候选法的视角来分析
〔1〕对全盘进行候选数的全面标记。

可以采用余数法作标记。手工打造全标是很费时间的
〔2〕观察第九列

数字 4 和 9,只出现在第九列 C9 中的 R2C9 和 R9C9 两个格中。
其中,R2C9 中还有数字 7;R9C9 还有数字 5。
〔3〕同单元内有 n 种不同的数字只能填入到 n 个单元格内,该些格中因为还有其它候选数很难辨认,因此称为隐性数组。
因此,数组 R29C9(49)称作隐性数组。
〔六〕特别说明
1、在上述举例中,通过余数法发现了显性数对,通过排除法发现了隐性数对。但是,并不是说,所有通过余数法得到的数组一定是显性数对,也可能是隐性数组。同样,并不是说,所有通过排除数法得到的数组一定是隐性数对,也可能是显性数组。
2、到底是显性数组还是隐性数组,要通过全标候选数来区分。单元格内包含数组本身的数字,不包含其他数字,就是显性数组。单元格内不仅包含数组本身的数字,还包含其他数字,就是隐性数组。
3、在直观法中发现数组是不容易的,相对来说,在候选数法中更容易发现数组。因此,数组技巧更多应用在候选数法中。
四、详解显性数组和隐性数组
〔一〕显性数组:同一区域下,n 个单元格内只数组有 n 种不同的数字。
1、显性数组是一种根据 “n 个单元格填 n 种候选数” 的情况,来确定删数和出数结论的技巧。
2、显性数组可以利用余数法对单元格进行点算,通过数数的操作进行数字的枚举,最终可以得到显性数组。
3、在标记候选数的情况下,可以明显的看到 n 个单元格中只有 n 种候选数。
4、显性数组按照数组规格,可有效使用的一共有 3 种:显性数对(双数组)、显性三数组(三链数)、显性四数组(四链数)。
〔二〕隐性数组:同一区域下,n 种不同的数字只能填入到 n 个单元格内。
1、隐性数组是一种根据 “当前行列宫内仅有 n 个单元格来填这 n 种候选数”,来确定删数和出数结论的技巧。
2、“隐性” 体现在 “必须通过排除才能看到,单元格内的填数情况标注出来无法立马确定”。隐性数组不能被直观的看到,需要进行分析才能观察到。可以通过排除的操作对位置进行枚举,最终可以得到隐性数组
3、隐性数组按照数组规格,可有效使用的一共有 3 种:隐性数对(双数组)、隐性三数组(三链数)、隐性四数组(四链数)。
〔三〕直观法解题时,由于没有标候选数的关系,所以观察到的数组很难判定其为显性或隐性。
1、因此解题时必须同时考虑删数及占位两种情形,才不致遗漏数对所能发挥的功效。
2、解题时若能从这两方面去思考,则数对解法可以发挥的威力会远远超乎你的想象。
五、数组的作用
〔一〕占位:n 种数字已经被 n 个单元格占用了,同一区域的其他格子就不能用了。
〔二〕删数:n 个单元格里只能有 n 种数字,这些单元格中的其他数字就可以删除了。
〔三〕显性数组和隐性数组在作用上的区别
1、对外:显性数组的作用是对所在宫和所在行列的其他相同候选数进行排除,他是对外排除的。
2、对内:隐性数组的作用,他不排除所在宫和所在行列的其他格里的相同候选数。他是对隐性数组所在的格内部的其他的候选数进行排除的,他是对内排除的。
本节实例答案

实例一:初盘

实例一:终盘

实例二:初盘

实例二:终盘
标签:候选,数字,填入,单元格,格子,数组,数独 From: https://www.cnblogs.com/LR--Gragon/p/sudoku-zs8tdx.html