监狱 - IPS99技术分享

标签：监狱连边囚犯 int 线段路径罪犯

题目链接：[JOISC 2022 Day1] 监狱

本题的思路并不刁钻，但十分考验代码能力，因此本蒟蒻尽量讲的仔细一点，尽量串联起思路与代码中的重点，当然也方便本人加深理解。

Analysis:

首先对于两个的罪犯，我们思考他们在什么情况下不合法，无非以下几种：

两个囚犯路径有重合，且相向而行。
两个囚犯路径呈包含与被包含关系。
两个囚犯路径有重合，但处理不当，使其在中途相遇。

\(\dots\)

我们发现这些限制条件只能提供一些类似于特殊判断的思路，而且限制三肉眼可见的不合理，那么我们只好换一种思路：从最后合法的方案入手。如果最后方案合法，就意味着有一种合理的先后顺序可以安排所有罪犯，使其不相遇且到达终点。

而囚犯们当然可以先安排一个囚犯走完他的路径，再同理安排另一个，这是因为每个囚犯的移动路径是独立的，要想判断最终情况是否合法，这要知道先后顺序，这与囚犯们谁先走完路径是无关的，故这种移动策略是合理的。

所以，我们去思考每个囚犯移动的先后顺序，不难得出以下两条简洁规整的性质：

如果 \(A\) 的起点在 \(B\) 的路径上，那么 \(A\) 必须先于 \(B\) 走。
如果 \(A\) 的终点在 \(B\) 的路径上，那么 \(B\) 必须先于 \(A\) 走。

由此答案也就呼之欲出了，我们根据这两条性质为各个囚犯连有向边表示他们的先后关系，暴力跳点，拓扑判环，如果成环就是不合法方案，那么你会获得一个 \(\Theta(n^2)\) 的连边建图，这样的复杂度在本题的数据范围下当然会被卡的十分拉跨，那么我们将思路优化一下，用线段树优化建图。

我们首先将原图的树复制两棵 \(S,T\)，约定用 \(S_x\)，\(T_x\) 表示原图中点 \(x\) 在这两棵树上的编号（原树的 dfs 序）。

对于 \(i\) 的路径：

我们从所有路径上的点在 \(S\) 上对应的点向 \(p_i\) 连边，代表起点在这些点上的人必须先于 \(i\) 走，为了传递限制，还需对每个 \(p_i\) 向 \(S_{s_i}\) （第 \(i\) 个罪犯的起点的编号）连边
我们从 \(p_i\) 向所有路径上的点在 \(T\) 上对应的点连边，代表 \(i\) 必须先于终点在这些点上的人走，为了传递限制，还需对每个 \(T_{t_i}\) （第 \(i\) 个罪犯的终点的编号）向 \(p_i\) 连边。

如果你还不是很明白，那我们不妨画个图辅助理解：

首先，我们先看非法的一组数据：

图长这样：

因为两条路径有重复，根据上文提到的性质，我们给两个人分别连边，发现成环，因此不合法。但是我们将其放在线段树上，又该怎么办？

首先按照线段树优化建图的套路，对原树按照 dfs 序建立两棵线段树，一颗为全是出边的”出树“，另一棵为全是入边的“入树”，按照上文提到的连边规则，我们不难连出这样一幅图：

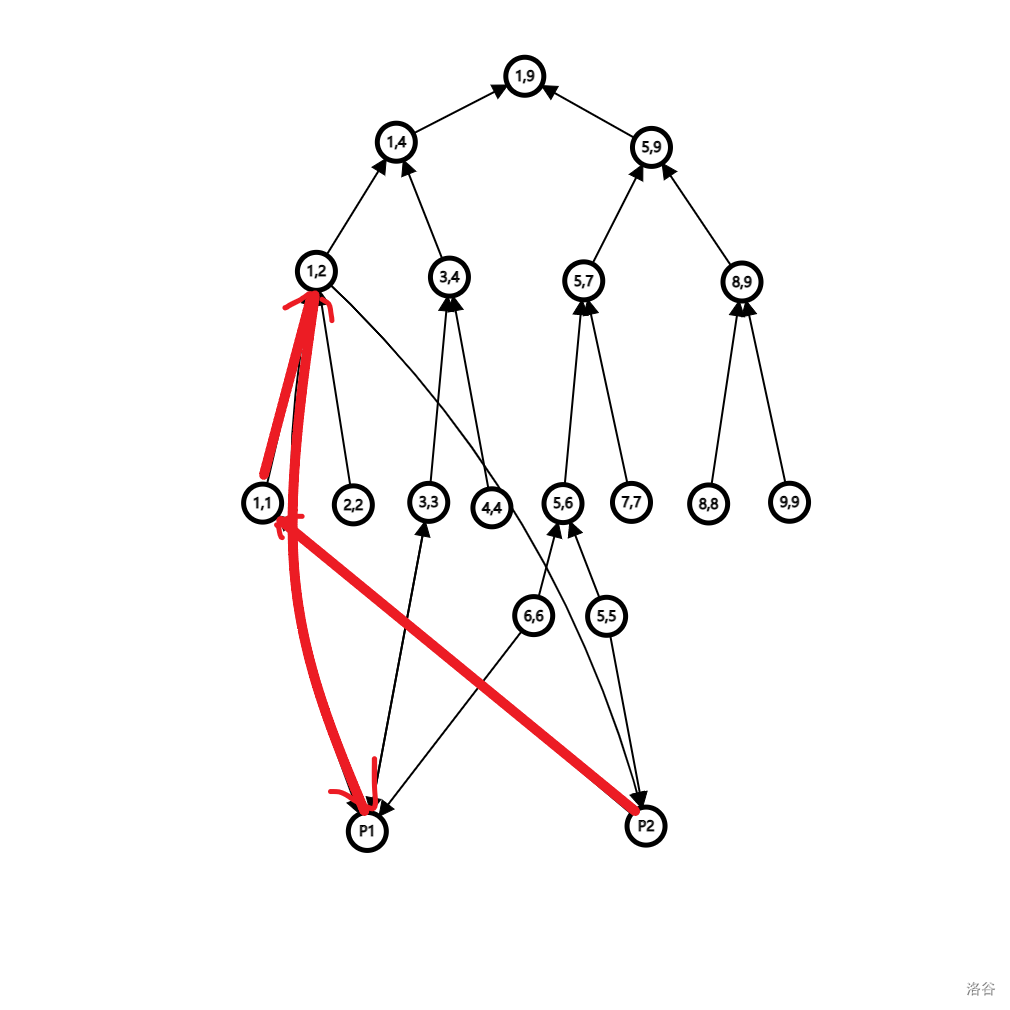
这是一棵“入树”，可以发现经过连边，\(P_2\) 罪犯可以向 \(P_1\) 罪犯连一条有向边，代表 \(P_2\) 与 \(P_1\) 的先后顺序，同理，我们再建一棵”出树“（这里不再给出图片），可以发现 \(P_1\) 罪犯又向 \(P_2\) 罪犯连出了另一条有向边，我们惊喜的发现：\(P_1\) 与 \(P_2\) 罪犯成环了！矛盾的出现意味着非法的诞生，那么我们愉快地将当前局面判为“非法”。

Achieve:

首先树剖求出 dfs 序及重链，然后线段树建出两棵树表示”出入树“，我们发现操作涉及区间对单点加边以及单点对区间加边，那么我们在跳重链的时候对两棵树进行操作，然后就是将单点对单点加边，最后拓扑判环，拜拜程序。

Attention:

两棵线段树实际上建的是同一个图的不同种边（废话）。
多测的清空记得精细化处理。
原树与线段树建图一定要区分清楚，不论是思路上还是代码上。

Code:

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N=5e6+5;
int n,m;
int deg[N];
int to[N<<1],nxt[N<<1],head[N<<1],tot1;
int to1[N<<1],head1[N<<1],nxt1[N<<1],tot;
void add1(int u,int v){
    to1[++tot]=v,nxt1[tot]=head1[u],head1[u]=tot;
    to1[++tot]=u,nxt1[tot]=head1[v],head1[v]=tot;
}
void add(int u,int v){
    // if(typ) swap(u,v);
    to[++tot]=v,nxt[tot]=head[u],head[u]=tot;
    deg[v]++;
}
int f[N],son[N],rev[N],top[N],dfn[N],siz[N],dep[N],cntd;
void dfs(int u,int fa){
    dep[u]=dep[fa]+1,siz[u]=1,f[u]=fa;
    for(int i=head1[u];i;i=nxt1[i]){
        if(to1[i]==fa) continue;
        dfs(to1[i],u);
        siz[u]+=siz[to1[i]];
        if(siz[to1[i]]>siz[son[u]]) son[u]=to1[i];
    }
}
void dfs2(int u,int tp){
    top[rev[dfn[u]=++cntd]=u]=tp;
    if(son[u]) dfs2(son[u],tp);
    for(int i=head1[u];i;i=nxt1[i]) if(to1[i]^f[u]&&to1[i]^son[u]) dfs2(to1[i],to1[i]);
}
int cnt(0);
int leaf[N][2];
struct SMT{
    #define lc t[pos].ls
    #define rc t[pos].rs
    #define mid ((l+r)>>1)
    struct Node{
        int ls,rs;
    }t[N<<2];
    void build(int &pos,int l,int r,int typ){
        pos=++cnt;
        if(l==r) return leaf[l][typ]=pos,void();
        t[pos].ls=t[pos].rs=0;
        build(lc,l,mid,typ);build(rc,mid+1,r,typ);
        if(typ) add(pos,lc),add(pos,rc);
        else add(lc,pos),add(rc,pos);
    }
    void update(int pos,int l,int r,int L,int R,int x,int typ){
        if(r<L||R<l||R<L) return;
        if(L<=l&&r<=R) return typ?add(x,pos):add(pos,x),void();
        update(lc,l,mid,L,R,x,typ);
        update(rc,mid+1,r,L,R,x,typ);
    }
    #undef lc
    #undef rc
    #undef mid
}S,T;
int trt,srt;
void update(int x,int y,int z){
    if(dep[x]<dep[y]) swap(x,y);
    if(dfn[y]<=dfn[x]&&dfn[x]<=dfn[y]+siz[y]-1){
        x=f[x];
        while(top[x]^top[y]){
            S.update(srt,1,n,dfn[top[x]],dfn[x],z,0);
            T.update(trt,1,n,dfn[top[x]],dfn[x],z,1);
            x=f[top[x]];
        }
        S.update(srt,1,n,dfn[y]+1,dfn[x],z,0);
        T.update(trt,1,n,dfn[y]+1,dfn[x],z,1);
    }else{
        x=f[x],y=f[y];
        while(top[x]^top[y]){
            if(dep[top[x]]<dep[top[y]]) swap(x,y);
            S.update(srt,1,n,dfn[top[x]],dfn[x],z,0);
            T.update(trt,1,n,dfn[top[x]],dfn[x],z,1);
            x=f[top[x]];
        }
        if(dfn[x]<dfn[y]) swap(x,y);
        S.update(srt,1,n,dfn[y],dfn[x],z,0);
        T.update(trt,1,n,dfn[y],dfn[x],z,1);
    }
}
bool topo(){
    queue<int> q;
    for(int i=1;i<=cnt;i++) if(!deg[i]) q.push(i);
    while(!q.empty()){
        int u=q.front();q.pop();
        for(int i=head[u];i;i=nxt[i]){
            deg[to[i]]--;
            if(!deg[to[i]]) q.push(to[i]);
        }
    }
    for(int i=1;i<=cnt;i++) if(deg[i]) return false;
    return true;
}
void clear(){
    memset(head1,0,sizeof(int)*(n+1));
    memset(head,0,sizeof(int)*(cnt+1));
    memset(son,0,sizeof(int)*(n+1));
    memset(deg,0,sizeof(int)*(cnt+1));
    tot=tot1=cnt=cntd=srt=trt=0;
}
int main(){
    //  freopen("prison.in","r",stdin);
    //  freopen("prison.out","w",stdout);
    int t;cin>>t;
    while(t-->0){
        clear();
        scanf("%d",&n);
        for(int i=2,u,v;i<=n;i++){
            scanf("%d%d",&u,&v);
            add1(u,v);
        }
        dfs(1,0),dfs2(1,1);
        S.build(srt,1,n,0);
        T.build(trt,1,n,1);
        scanf("%d",&m);
        for(int i=1,s,t;i<=m;i++){
            scanf("%d%d",&s,&t);
            cnt++;
            add(leaf[dfn[t]][0],cnt),add(cnt,leaf[dfn[s]][0]);
            add(leaf[dfn[t]][1],cnt),add(cnt,leaf[dfn[s]][1]);
            update(s,t,cnt);
        }
        puts(topo()?"Yes":"No");
    }
}

感谢阅读！！！

标签：监狱,连边,囚犯,int,线段,路径,罪犯
From： https://www.cnblogs.com/shen666zxcmt/p/17648211.html

监狱

Analysis:

Achieve:

Attention:

Code:

相关文章

赞助商

阅读排行