算是一道很经典的题了,所以决定写博客
设最后选出的四种生物个数分别是\(A\),\(B\),\(C\),\(D\),则最后的答案显然是\((A-B)^2+(C-D)^2\)
我们不妨把一个生物群\(a_i\),\(b_i\),\(c_i\),\(d_i\)看成向量\((a_i-b_i,c_i-d_i)\),则原题就变成了从\(n\)个向量中选若干个,使得这些向量的和的模长的平方最大
然后看到这题ABC139F
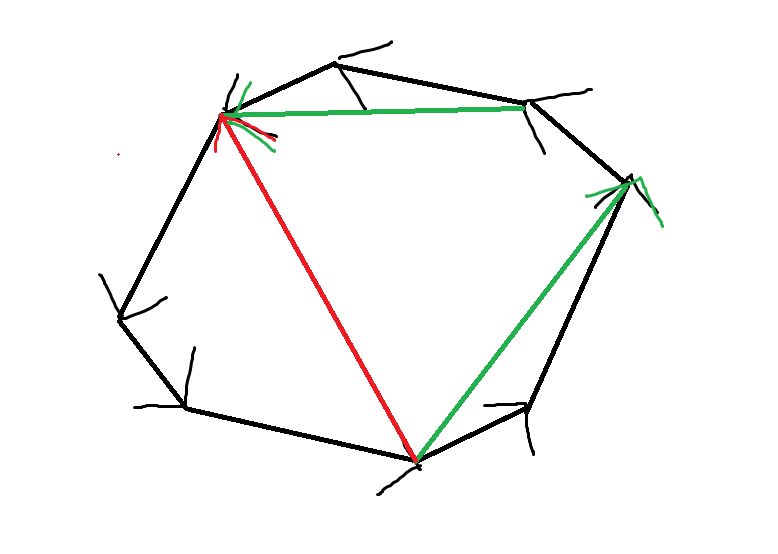
我们把这\(n\)个向量加入一个集合中,按照幅角排序,能够得到半个或一个凸包
最终的答案一定是凸包顶点上的一对点\((x,y)\)之间的距离,因为如果答案是凸包的两个部分合起来,我们不如直接把这两个位置中间的所有向量都加入答案,这样得到的总是更优的
如图,两个绿色向量之和一定没红色向量优
方法1:
\(O(n^2)\)的枚举肯定是不现实的,但我们发现从一个向量开始绕一圈后当遇到和他平行但方向相反的向量时,把他删掉答案肯定更优
如图,\(\max{(|v_1|,|v_2|)} \geq |v_3|\)
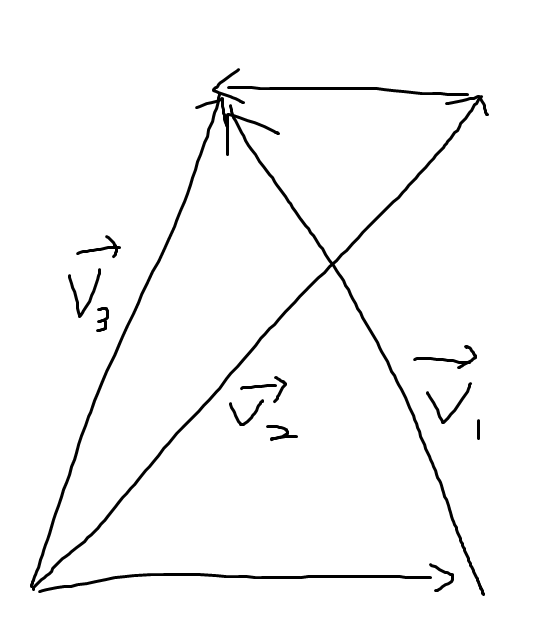
我们可以用几何方法,因为上下两个向量平行,所以他们和\(v_3\)形成的夹角一定有一个\(\geq 90^。\),其一定比\(v_3\)的模长要大
所以我们可以把这\(n\)个向量的反向量也加入凸包中,这样当存在一个向量和这个向量平行之前这个向量就会被它的反向量抵消掉
当然这样还存在一个问题,可能刚开始的时候把反向量加入了答案,但现实的答案时不能只使用反向量的
因此如果存在一个反向量\(v'_i\)的模角>\(v_i\),则我们先把前缀向量和+=\(v_i\),来保证反向量一定能起到删除作用
复杂度瓶颈在于排序,最终复杂度\(O(nlogn)\)
方法2:
我们发现这个区间肯定是有单调性的,所以我们可以使用双指针
用法和上面做法类似,如果碰到和他平行的就把左端点+1即可
同样也是\(O(nlogn)\),但方法1好写很多
标签:CF1841F,加入,凸包,答案,平行,我们,向量 From: https://www.cnblogs.com/fox-konata/p/17645394.html