做题笔记Ⅱ
贪心
CF1764C
题目描述
有一些点,每个点有一个点权 \(a_i\), 你可以在任意两个点间连边。最终你连成的图需要满足:不存在点 \(u, v, w\),满足 \(a_u\leq a_v\leq a_w\) 且边 \((u, v), (v, w)\) 存在。求最多能连的边数。
题解
考虑到题目所求是一个有序的三元组,所以我们习惯性地对序列进行排序。我们不难发现,在序列中一个点连接的右边的点,就不能再连左边的点,反之亦然。
因此,为了保证连接的有序性,我们很容易发现构造的连边方式是二分图匹配的。
对于二分图而言,我们想要连边方式更多,一种可取的想法是构造完全二分图。
对于朴素的情况,我们枚举断点。将序列分成左右两份,注意一种权只能分在左右一边,接着使用乘法原理计算边数即可,可以证明,这是二分图中最优的情况。
此外,对于颜色全部相同的特殊情况,我们无法构造完全二分图。这时,我们只需要两两匹配即可。
代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+100;
int t,n,a[N],ans;
bool check()
{
for(int i=2;i<=n;i++)
{
if(a[i]!=a[i-1])
return false;
}
cout<<n/2<<endl;
return true;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>t;
while(t--)
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
sort(a+1,a+1+n);
if(check()==true)
continue;
ans=0;
for(int i=1;i<=n;i++)
{
int l=upper_bound(a+1,a+1+n,a[i])-a-1;
ans=max(ans,l*(n-l));
}
cout<<ans<<endl;
}
return 0;
}
P9207
题目描述
有一台计算器,使用 \(k\) 位的带符号整型来对数字进行存储。也就是说,一个变量能够表示的范围是 \([-2^{k-1},2^{k-1})\)。现在我们希望使用该计算器计算一系列数 \(a_1,a_2,\cdots,a_n\) 的和。计算的伪代码如下:

由于奇怪的特性,如果两个变量在相加时得到的结果在 \([-2^{k-1},2^{k-1})\) 之外,即发生了溢出,那么这台计算器就会卡死,再也无法进行计算了。
为了防止这样的事情发生,一个变通的方法是更改 \(a_i\) 的排列顺序。容易发现这样不会改变计算出的和的值。
不过,可能不存在一种方案,使得计算出这 \(n\) 个数并且计算机不爆炸。但我们还是希望,计算出尽量多的数字的和。
题解
我们考虑相加的结果可能因过小或过大而超界,因此我们希望维护一个基于0的平衡。
我们考虑分别按正负数分类,并按绝对值排序。贪心判断,加正负数两者谁更接近原点。
本题的一大坑点在于给定的区间是左闭右开,这点在特判时需要注意。
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=510;
int n,k,a[N],b[N],l1,l2,z1,z2,ans,no;
bool cmp(int x,int y)
{
return x>y;
}
bool check(int x)
{
if(x<0&&abs(x)<=(1<<k))
return true;
if(x>=0&&abs(x)<(1<<k))
return true;
return false;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>k;
k--;
for(int i=1;i<=n;i++)
{
int x;
cin>>x;
if(x<0)
b[++l2]=x;
else
a[++l1]=x;
}
sort(a+1,a+1+l1);
sort(b+1,b+1+l2,cmp);
for(int i=1;i<=n;i++)
{
if(z1==l1)
{
for(int i=z2+1;i<=l2;i++)
{
if(check(no+b[i])==true)
{
no+=b[i];
ans++;
}
else
break;
}
break;
}
if(z2==l2)
{
for(int i=z1+1;i<=l1;i++)
{
if(check(no+a[i])==true)
{
no+=a[i];
ans++;
}
else
break;
}
break;
}
if(abs(no+a[z1+1])<abs(no+b[z2+1]))
{
no+=a[++z1];
if(check(no)==true)
ans++;
else
break;
}
else
{
no+=b[++z2];
if(check(no)==true)
ans++;
else
break;
}
}
cout<<ans;
return 0;
}
P3918
题目描述
神犇航空开展了一项载客特技飞行业务。每次飞行长 \(n\) 个单位时间,每个单位时间可以进行一项特技动作,可选的动作有 \(k\) 种,每种动作有一个刺激程度 \(c_i\)。如果连续进行相同的动作,乘客会感到厌倦,所以定义某次动作的价值为(距上次该动作的时间) $ \times c_i$,若为第一次进行该动作,价值为 \(0\)。安排一种方案,使得总价值最大。
题解
由题意,一个动作的贡献依赖于距上次做该动作的时间,因此,只做一次是不会产生贡献的。
考虑两次时会产生左右端点的距离,而多次同样为左右端点的距离。显然对于每个动作只需进行两次即可。
我们根据贪心的思想,显然想要 \(c\) 更大的动作相距距离更长,因此最大的动作应放在时间轴两端执行,其余则依次向内延展。
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+100;
int n,k,c[N],z,ans;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>k;
for(int i=1;i<=k;i++)
{
cin>>c[i];
}
sort(c+1,c+1+k,greater<int>());
for(int i=n-1;i>=1;i-=2)
{
ans+=i*c[++z];
}
cout<<ans;
return 0;
}
P9209
题目描述
有一个包含 \(n\) 个停车位的停车场,里面的停车位排成了一排,最左边和最右边都是墙壁。
有 \(n\) 辆车要按顺序依次停入这个停车场,在停入第 \(i\) 辆车时,这辆车要停入的位置左右两边的空位越多,停进去需要的时间也就会越少,具体地,如果其左边连续的空位数量为 \(l\),其右边连续的空位数量为 \(r\),那么停入该辆车所需时间为 \(W_i-L_i\cdot l-R_i\cdot r\),其中 \(W_i,L_i,R_i\) 会给出(特别的,停车所需要的时间不会是负数,所以我们保证 \(W_i\ge L_i\cdot n+R_i\cdot n\))。
对于连续空位的解释:例如,下图中箭头所指位置左边连续空位为 \(1\),右边连续空位为 \(2\)。
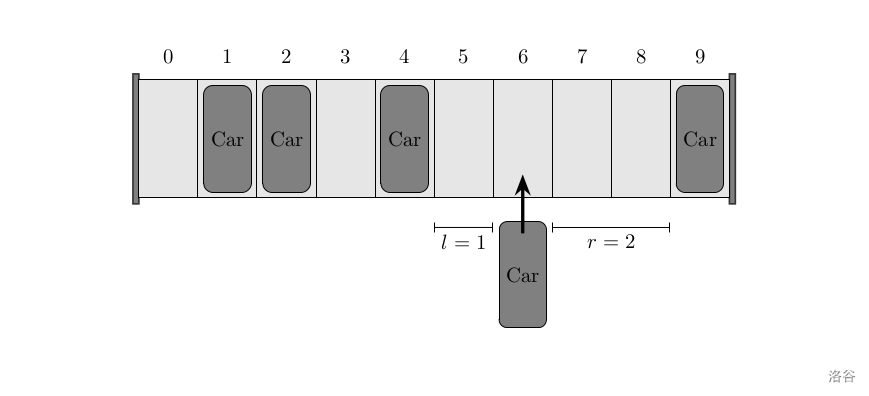
请依次确定每一辆车停入的位置,使得停入所有车所需时间最小。
题解
题目保证了 \(W_i\ge L_i\cdot n+R_i\cdot n\) 这一点保证了 \(L\) 和 \(R\) 对于贡献的有效性。
我们考虑在插入一辆车时怎样最优,显然选择一个最大的区间,并将汽车放在 \(LR\) 更大的一侧。
接着我们考虑一辆车对后续车怎样最优,显然为后续车辆维持一个完整较大的区间是最优的。
因此本题将汽车停放于边缘的贪心思路就形成了。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+100;
int n,w[N],L[N],R[N],ans;
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>w[i];
}
for(int i=1;i<=n;i++)
{
cin>>L[i];
}
for(int i=1;i<=n;i++)
{
cin>>R[i];
}
for(int i=1;i<=n;i++)
{
ans+=w[i]-max(L[i],R[i])*(n-i);
}
cout<<ans;
return 0;
}
P6155
题目描述
给定一个长度为 \(n\) 的整数序列 \(a_i\),再给定一个长度为 \(n\) 的整数序列 \(b_i\)。
你可以进行一些修改,每次你可以将一个 \(a_i\) 增加 \(1\),花费为 \(b_i\),你需要使所有的 \(a_i\) 不相等,且同时满足花费最少。
但 zbw 认为太过简单,于是他规定,你可以在修改前进行无限次如下操作:交换 \(b_i,b_j(1 \leq i,j \leq n)\)。
求最小的花费。
由于答案可能很大,请输出答案对 \(2^{64}\) 取模后的值。
题解
考虑到 \(a_i\) 增加1可能会与更大数相同,从而触发连锁反应,我们先对原数组排序。接着我们根据贪心的思想,对于相同的数,应当为其找到操作次数较小的,更小的落脚点。且更多的数应当更快的找到落脚点。由于我们已经给原数组排序,我们不难发现遍历过程中需要修改的数是后进先出的,我们可以用栈维护。最后我们统计修改次数,给次数越多的附上越小的 \(b\) 即可。
代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+100;
int n,a[N],b[N],c[N];
stack<int>st;
unsigned long long ans;
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
for(int i=1;i<=n;i++)
{
cin>>b[i];
}
sort(a+1,a+1+n);
for(int i=2;i<=n;i++)
{
if(a[i]==a[i-1])
{
st.push(i);
}
for(int j=a[i-1]+1;j<a[i]&&st.size()!=0;j++)
{
c[st.top()]=j-a[st.top()];
st.pop();
}
}
for(int i=a[n]+1;st.size()!=0;i++)
{
c[st.top()]=i-a[st.top()];
st.pop();
}
sort(c+1,c+1+n);
sort(b+1,b+1+n,greater<int>());
for(int i=1;i<=n;i++)
{
ans+=b[i]*c[i];
}
cout<<ans;
return 0;
}