首页 > 其他分享 >栈与队列

栈与队列

时间：2023-08-17 23:12:59浏览次数：41  
标签：return val 队列 Queue int data size

栈与队列

前言

 栈与队列作为线性表结构的代表，在计算机领域应用广泛。我们耳熟能详的系统栈，进程处理等计算机操作系统底层实现原理都是间接或者直接使用了相关数据结构或其思想，下面让我们来介绍这两种数据结构。

栈

结构定义

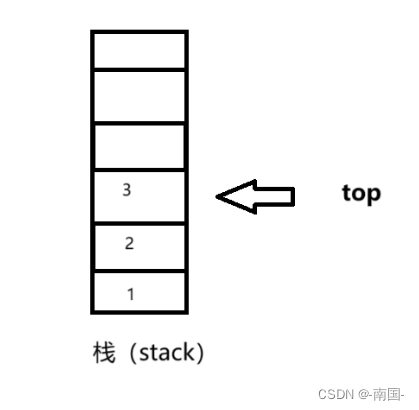
  栈(stack)是限定仅在表尾进行插入或者删除的线性表。对于栈来说，表尾端称为栈顶（top），表头端称为栈低（bottom）。不含元素的空表称为空栈。因为栈限定在表尾进行插入或者删除，所以栈又被称为后进先出的线性表（简称LIFO:Last in, First out.结构）。
在这里插入图片描述

  • 定义结构体
typedef struct Stack {
    int *data;
    int top, size;
}Stack;

结构操作

  • 初始化（init）
//初始化
Stack *init(int n) {
    Stack *s = (Stack *)malloc(sizeof(Stack));
    s->data = (int *)malloc(sizeof(int) * (n + 10));
    s->top = -1;
    s->size = n;
    return s;
}
  • 压栈、入栈（push）
//入栈
int push(Stack *s, int val) {
    if (s == NULL) return 0;
    if (s->top + 1 == s->size) {
        if (!expand(s)) return 0;
        printf("expand Stack->size is successful!\n");
    }
    s->data[++s->top] = val;
    return 1;
}
  • 获取栈顶元素（top/front）
//获取队首元素
int top(Stack *s) {
    if (empty(s)) return -1;
    return s->data[s->top];
}
  • 扩容操作（expand）
//扩容
int expand(Stack *s) {
    int exp_size = s->size;
    int *p;
    while (exp_size) {
        p = (int *)realloc(s->data, (s->size + exp_size));
        if (p) break;
        exp_size /= 2;
    }
    if (p == NULL) return 0;
    s->data = p;
    s->size += exp_size;
    return 1;
}
  • 销毁（clear）
//销毁
void clear(Stack *s) {
    if (s == NULL) return ;
    free(s->data);
    free(s);
    return ;
}
  • 判空（empty）
//判空操作
int empty(Stack *s) {
    return s->top == -1;
}
  • 出栈、弹栈（pop）
//出栈
int pop(Stack *s) {
    if (s == NULL) return 0;
    if (empty(s)) return 0;
    s->data[s->top--];
    return 1;
}

完整代码（栈）

#include<stdio.h>
#include<stdlib.h>
#include<time.h>
//顺序栈：初始化、销毁、获取队首元素、判空操作、入栈、出栈

typedef struct Stack {
    int *data;
    int top, size;
}Stack;

//初始化
Stack *init(int n) {
    Stack *s = (Stack *)malloc(sizeof(Stack));
    s->data = (int *)malloc(sizeof(int) * (n + 10));
    s->top = -1;
    s->size = n;
    return s;
}

//判空操作
int empty(Stack *s) {
    return s->top == -1;
}

//获取队首元素
int top(Stack *s) {
    if (empty(s)) return -1;
    return s->data[s->top];
}


//扩容
int expand(Stack *s) {
    int exp_size = s->size;
    int *p;
    while (exp_size) {
        p = (int *)realloc(s->data, (s->size + exp_size));
        if (p) break;
        exp_size /= 2;
    }
    if (p == NULL) return 0;
    s->data = p;
    s->size += exp_size;
    return 1;
}

//入栈
int push(Stack *s, int val) {
    if (s == NULL) return 0;
    if (s->top + 1 == s->size) {
        if (!expand(s)) return 0;
        printf("expand Stack->size is successful!\n");
    }
    s->data[++s->top] = val;
    return 1;
}

//出栈
int pop(Stack *s) {
    if (s == NULL) return 0;
    if (empty(s)) return 0;
    s->data[s->top--];
    return 1;
}

//销毁
void output(Stack *s) {
    if (s == NULL || empty(s)) return ;
    printf("[");
    for (int i = 0; i <= s->top; i++) {
        i && printf(", ");
        printf("%d", s->data[i]);
    }
    printf("] <== Stack[%d]\n", s->top + 1);
    return ;
}

//销毁
void clear(Stack *s) {
    if (s == NULL) return ;
    free(s->data);
    free(s);
    return ;
}

int main () {
    #define max_op 20
    int op, val;
    srand(time(0));
    Stack *s = init(10);//测试
    for (int i = 0; i < max_op; i++) {
       op = rand() % 4;
       val = rand() % 100 + 1;
       switch (op) {
           case 0:
           case 1:
           case 2: {
               printf("push val(%d) to the Stack is %s!\n", val, push(s, val) ? "YES" : "NO");
           } break;
           case 3: {
               val = top(s);
               printf("pop val(%d) from the Stack is %s!\n", val, pop(s) ? "YES" : "NO");
           } break;
        }
        output(s);
    }
    clear(s);
    #undef max_op
    return 0;
}

队列

结构定义

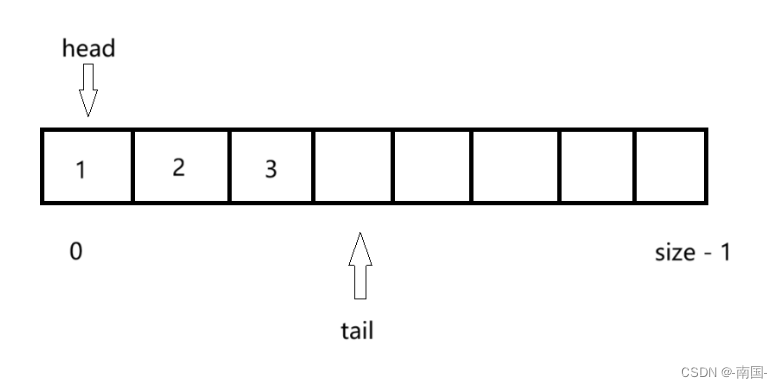
  相比于栈结构而言，队列是队首出队，队尾入队的受限线性表结构。特点是先入先出（LILO）
在这里插入图片描述

  • 定义结构体
typedef struct Queue {
    int *data;
    int head, tail, size;
}Queue;

结构操作

  • 初始化（init）
//初始化队列
Queue *init(int n) {
    Queue *q = (Queue *)malloc(sizeof(Queue));
    q->data = (int *)malloc(sizeof(int) * (n + 10));
    q->head = q->tail = 0;
    q->size = n;
    return q;
}
  • 销毁（clear）
//销毁
void clear(Queue *q) {
    if (q == NULL) return ;
    free(q->data);
    free(q);
    return ;
}
  • 判空（empty）
//判空操作
int empty(Queue *q) {
    if (q == NULL) return 1;
    return q->head == q->tail;
}
  • 获取队首元素（front）
//获取队首元素
int front(Queue *q) {
    if (q == NULL || empty(q)) return -1;
    return q->data[q->head];
}
  • 入队（push）
//入队操作
int push(Queue *q, int val) {
    if (q == NULL) return 0;
    if (q->tail + 1 == q->size) {
        if (!expand(q)) return 0;
        printf("expand the Queue size is successful!\n");
    }
    q->data[q->tail++] = val;
    return 1;
}
  • 出队（pop）
//出队操作
int pop(Queue *q) {
    if (q == NULL || empty(q)) return 0;
    q->head++;
    return 1;
}

循环队列

  • 循环队列实现思路？
    • 队列再结构体的属性中定义一个cnt变量，即q→cnt 。
    • 当head == q→size 时 使得head -= q→size；tail 亦然。
    • 当需要遍历队列时，（0 → q→cnt） ⇒ q→data[（q→head + i）% q→size];即可

完整代码（队列、循环队列）

  • 队列
#include<stdio.h>
#include<stdlib.h>
#include<time.h>


//顺序表队列:初始化、销毁、扩容、获取队首元素、判空、入队、出队
typedef struct Queue {
    int *data;
    int head, tail, size;
}Queue;

//初始化队列
Queue *init(int n) {
    Queue *q = (Queue *)malloc(sizeof(Queue));
    q->data = (int *)malloc(sizeof(int) * (n + 10));
    q->head = q->tail = 0;
    q->size = n;
    return q;
}

//判空操作
int empty(Queue *q) {
    if (q == NULL) return 1;
    return q->head == q->tail;
}

//获取队首元素
int front(Queue *q) {
    if (q == NULL || empty(q)) return -1;
    return q->data[q->head];
}

int expand(Queue *q) {
    int exp_size = q->size;
    int *p;
    while (exp_size) {
        p = (int *)realloc(q->data, (exp_size + q->size));
        if (p) break;
        exp_size /= 2;
    }
    if (p == NULL) return 0;
    q->data = p;
    q->size += exp_size;
    return 1;
}

//入队操作
int push(Queue *q, int val) {
    if (q == NULL) return 0;
    if (q->tail + 1 == q->size) {
        if (!expand(q)) return 0;
        printf("expand the Queue size is successful!\n");
    }
    q->data[q->tail++] = val;
    return 1;
}

//出队操作
int pop(Queue *q) {
    if (q == NULL || empty(q)) return 0;
    q->head++;
    return 1;
}

//遍历
void output(Queue *q) {
    if (q == NULL || empty(q)) return ;
    printf("[");
    for (int i = q->head; i < q->tail; i++) {
        i != q->head && printf(",");
        printf("%d", q->data[i]);
    }
    printf("] <== Queue[%d]\n", q->tail - q->head);
    return ;
}

//销毁
void clear(Queue *q) {
    if (q == NULL) return ;
    free(q->data);
    free(q);
    return ;
}

int main() {
    srand(time(0));
    int op, val;
    #define max_op 20
    Queue *q = init(10);
    for (int i = 0; i < max_op; i++) {
        op = rand() % 4;
        val = rand() % 100 + 1;
        switch(op) {
            case 0:
            case 1:
            case 2: {
                printf("push val(%d) to the Queue is %s!\n", val, push(q, val) ? "YES" : "NO");
            } break;
            case 3: {
                val = front(q);
                printf("pop front(%d) from the Queue is %s!\n", val, pop(q) ? "YES" : "NO");
            } break;
            
        }
        output(q);
    }
    clear(q);
    #undef max_op
    return 0;
}
  • 循环队列
#include<stdio.h>
#include<stdlib.h>
#include<time.h>

//循环队列:初始化、销毁、获取队首元素、判空操作、出队、入队、遍历
typedef struct Queue{
    int *data;
    int head, tail, size, cnt;
}Queue;

//初始化
Queue *init(int n) {
    Queue *q = (Queue *)malloc(sizeof(Queue));
    q->data = (int *)malloc(sizeof(int) * (n + 5));
    q->head = q->tail = q->cnt = 0;
    q->size = n;
    return q;
}

//判空
int empty(Queue *q) {
    return q->cnt;
}

//获取队首元素
int front(Queue *q) {
    if (q == NULL || !empty(q)) return -1;
    return q->data[q->head];
}

//入队
int push(Queue *q, int val) {
    if (q == NULL) return 0;
    if (q->cnt == q->size) return 0;//队列满了
    q->data[q->tail++] = val;
    if (q->tail == q->size) q->tail -= q->size;
    q->cnt++;
    return 1;
}
//出队
int pop(Queue *q) {
    if (q == NULL || !empty(q)) return 0;
    q->head++;
    if (q->head == q->size) q->head -= q->size;
    q->cnt--;
    return 1;
}

//遍历
void output(Queue *q) {
    if (q == NULL) return ;
    printf("[");
    for (int i = 0; i < q->cnt; i++) {
        i && printf(", ");
        printf("%d", q->data[(q->head + i) % q->size]);
    }
    printf("] <== Queue[%d]\n", q->cnt);
}

//销毁
void clear(Queue *q) {
    if (q == NULL) return ;
    free(q->data);
    free(q);
    return ;
}

int main() {
    srand(time(0));
    #define max_op 30
    Queue *q = init(10);  
    int op, val;
    for (int i = 0; i < max_op; i++) {
        op = rand() % 4;
        val = rand() % 100 + 1;
        switch (op) {
            case 0:
            case 1:
            case 2: {
                printf("Push val(%d) to the Queue is %s!\n", val, push(q, val) ? "YES" : "NO");
            } break;
            case 3: {
                val = front(q);
                printf("Pop val(%d) from the Queue is %s!\n", val, pop(q) ? "YES" : "NO");
            } break;
        }
        output(q);
    }
    #undef max_op
    clear(q);
    return 0;
}

标签：return,val,队列,Queue,int,data,size
From： https://www.cnblogs.com/wDao1/p/17639147.html

相关文章

  • 队列的实现方式（先进先出 FIFO）--环形队列
    博客地址：https://www.cnblogs.com/zylyehuo/#-*-coding:utf-8-*-classQueue:def__init__(self,size=100):self.queue=[0for_inrange(size)]self.size=sizeself.rear=0#队尾指针self.front=0#队首指针......
  • 队列的内置模块（deque）--双向队列
    博客地址：https://www.cnblogs.com/zylyehuo/#-*-coding:utf-8-*-fromcollectionsimportdequeq=deque([1,2,3,4,5],5)q.append(6)#队尾进队print(q.popleft())#队首出队#用于双向队列q.appendleft(1)#队首进队q.pop()#队尾出队......
  • 利用队列的内置模块（deque）模拟 Linux 下的 tail 命令（输出文件中最后几行的内容）
    博客地址：https://www.cnblogs.com/zylyehuo/#-*-coding:utf-8-*-fromcollectionsimportdequedeftail(n):#n：指定输出文件中最后几行withopen('test.txt','r')asf:q=deque(f,n)returnqforlineintail(5):print......
  • 栈和队列
    栈和队列1，栈(stack)栈是限定仅在表尾进行插入或者删除操作的线性表栈 :线性表->一对一的关系-》数组链表栈是有限制的线性表(阉割版的线性表)栈更重要的是一种思想先进后出，后进先出 在程序设计或算法中，会经常用到这种思想“撸串”“死胡同堵车”“压子弹” 栈顶(top)：进行插入或......
  • RabbitMq的死信队列
    参考博客：https://blog.csdn.net/weixin_59074080/article/details/130673121https://blog.csdn.net/m0_46979453/article/details/127229005https://zhuanlan.zhihu.com/p/582787597?utm_id=0什么是死信队列正常情况下，一条消息自生产者发布到broke，然后转发到队列中，最后被订阅......
  • 【单调队列】 单调队列的“扫描线”理解
    【单调队列】单调队列的“扫描线”理解  “如果一个选手比你小还比你强，你就可以退役了。”——单调队列的原理比你强，而且比你影响时间更长。某种意义上，数学思维是生活中的思考的延伸。  算法学习笔记(66):单调队列。引用Pecco的算法笔记。  在这里给出一种扫描线......
  • 3.1 C++ STL 双向队列容器
    双向队列容器（Deque）是C++STL中的一种数据结构，是一种双端队列，允许在容器的两端进行快速插入和删除操作，可以看作是一种动态数组的扩展，支持随机访问，同时提供了高效的在队列头尾插入和删除元素的操作。Deque双向队列容器与Vector非常相似，它不但可以在数组尾部插入和删除元素，还可以在......
  • 3.1 C++ STL 双向队列容器
    双向队列容器（Deque）是C++STL中的一种数据结构，是一种双端队列，允许在容器的两端进行快速插入和删除操作，可以看作是一种动态数组的扩展，支持随机访问，同时提供了高效的在队列头尾插入和删除元素的操作。Deque双向队列容器与Vector非常相似，它不但可以在数组尾部插入和删除元素，还可以在......
  • 代码随想录算法训练营第十三天|单调数列：滑动窗口最大值(力扣239.)、优先级队列：前k个高
    单调数列：滑动窗口最大值(力扣239.)给定滑动窗口的范围，求每个滑动窗口范围内的最大值使用单调队列实现对于最大值数字前面的数字不存入数列，对于最大值数字后面的数字存入数列中单调队列中数字的大小呈递减顺序pop(value)：如果窗口移除的元素等于单调队列的队口元素，则pop；否则什......
  • Redis专题-队列
    Redis专题-队列首先，想一想Redis适合做消息队列吗？1、消息队列的消息存取需求是什么？redis中的解决方案是什么？无非就是下面这几点：0、数据可以顺序读取1、支持阻塞等待拉取消息2、支持发布/订阅模式3、重新消费4、消息不丢失5、消息可堆积那我们来看看redis怎么满足这些需......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99