【单调队列】 单调队列的“扫描线”理解

  “如果一个选手比你小还比你强，你就可以退役了。”——单调队列的原理

• 比你强，而且比你影响时间更长。
• 某种意义上，数学思维是生活中的思考的延伸。

  算法学习笔记(66): 单调队列。引用 Pecco 的算法笔记。

  在这里给出一种扫描线的理解。

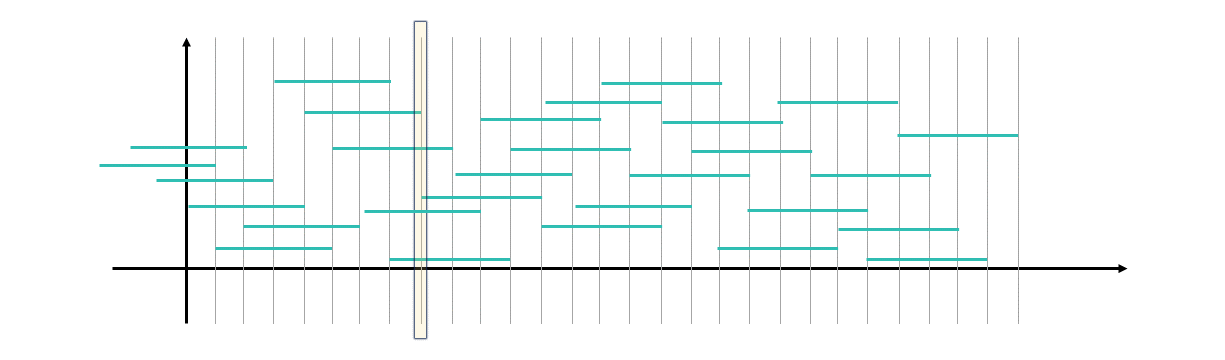
  我们以滑动窗口长度为 5，维护区间最大值为例子。

  图中横轴表示数组元素位置，纵轴表示数组元素大小，线表示每个数字的影响范围，对应记录的是长度为 k 的滑动窗口区间起点。因此，线段的右端点就是数组元素本身的位置。滑动窗口在图中仅仅需要标出起点的位置（一根竖线），就可以知道有哪些数字了。

  我们考虑后前后两段线。假如后一段大于等于前一段，那么后一段的影响未来范围比前一段更长，就可以在未来一直压着前一段。于是前一段没用了，弹出。（也就是说你预先考虑了一下未来的情况，然后弹出了）假如后一段小于前一段，虽然在过去和未来有限的时间里，前一段会压着后一段，但是后一段仍有不被压着的时候，因此后一段需要保留。

  当我们再直接观察队列中的弹出操作时候，就可以理解，弹出是因为之前的数影响范围被当前的更大的数字覆盖掉了。前面不弹出的是因为还有影响的可能。

  在这个问题中，序列本身是没有方向的，从左向右或者从右向左都行。我们进行滑动窗口的时候，需要规定一个方向。这个方向是无所谓的，但是一旦有了方向，这其中包含的已知到未知推导过程中前后顺序的维护信息，导致了单调队列的“覆盖”与弹出。剩下的“可能有贡献”的元素需要留着。删除不可能的，保留可能的，最后在某一时刻，从所有可能的中，选出确定的。

  为什么单调队列是单调的？我们考虑开始的时候用一个普通队列来维护，前后顺序是元素在序列中的顺序。每加入一个元素的时候，找一遍队列中的小于它的元素，删掉，再加入末尾（因为队列前后顺序和序列前后顺序是一样的）。这时候，查找就找这个队列里面的最大值。弹出照常。这两个操作现在还都是 \(O(k)\) 的。\(k\) 是滑动窗口长度。

  现在我们归纳地证一下。一个元素是有序的；对于新来的元素，改变一下操作顺序，先插入这个序列的正确排序的位置，再删除。有序序列删掉一些数还有序。于是 \(n\) 可以推 \(n+1\)。于是就都成立了。然后就有 \(O(1)\) 的取最大值和总和 \(O(n)\) 的插入删除操作了。\(n\) 是序列长度。