模拟退火算法中的退火过程是什么
这是一篇笔记,是对于B站up主马少平的视频(第四篇 如何用随机方法求解组合优化问题(四))的学习与记录。
这篇笔记还没有介绍到模拟退火算法,而是记录退火这一物理过程以及相关的公式。
最主要的内容是如何将退火过程的特点迁移到后续的算法设计中。
退火是什么
退火是固体物理学中的一个概念,它描述了固体材料在高温下逐渐冷却的过程,以使其从高能态逐渐转变为低能态。这个概念在模拟退火算法中得到了应用,用于寻找问题的最优解。
退火有以下过程:
- 加热阶段(高温阶段):在退火过程开始时,固体物体会被加热到非常高的温度。高温会使原子或分子的热运动剧烈,突破原本的位置限制。这种高温状态下,固体处于高能态,原子或分子的位置非常不稳定。
- 冷却阶段(退火阶段):随着时间的推移,温度逐渐降低。在温度逐渐降低的过程中,原子或分子的热运动减缓,逐渐趋向于更稳定的位置。随着温度的降低,固体会逐渐从高能态转变为低能态,原子或分子逐渐排列成更有序的结构。
- 冷却到基底温度(低温阶段):当温度足够低时,固体达到了最低能态,原子或分子的运动几乎停止,形成了稳定的结晶态。此时,固体的内部结构和排列达到了最优状态,对应着系统的全局最优解。
在模拟退火算法中,这个物理过程被用来模拟在解空间中寻找最优解的过程。算法从一个初始解(高温状态)开始,随机生成新的解(状态),并根据一定的准则决定是否接受新解。随着算法的迭代,模拟退火算法会逐渐减小“温度”,也就是接受劣解的概率,从而使算法在解空间中逐渐趋向于全局最优解,就像实际的退火过程一样。
退火过程
在退火过程中,状态转换的标准为:
-
如果 \(\Delta E \le 0\) ,则新状态被接受;
-
如果 \(\Delta E > 0\) ,则新状态被接受的概率为:
\[P = e^{-\frac{\Delta E}{KT}} \]
其中 \(\Delta E\) 是新状态的内能和初始状态的内能的差值,\(T\) 是绝对温度,\(K>0\) 是玻尔兹曼常数。
在给定的温度 \(T\) 下,当进行足够多次的状态转换后,系统将达到一种热平稳状态。
此时系统处于某个状态 \(i\) 的概率 \(P_i(T)\) 由 Boltzmann 分布给出:
\[P_i(T)=\frac{e^{-\frac{E(i)}{KT}}}{Z_T} \]其中 \(Z_T=\sum\limits_{j\in S}e^{-\frac{E(j)}{KT}}\) 为归一化因子。
退火过程分析
同一温度下两个内能不同的状态
-
假设两个状态的内能 \(E(i)<E(j)\):
\[\begin{align*} P_i(T)-P_j(T) &= \frac{e^{-\frac{E(i)}{KT}}}{Z_T} - \frac{e^{-\frac{E(j)}{KT}}}{Z_T} \\ &= \frac{1}{Z_T}e^{-\frac{E(i)}{KT}} \left( 1-\frac{e^{-\frac{E(j)}{KT}}}{e^{-\frac{E(i)}{KT}}} \right ) \\ &= \frac{1}{Z_T}e^{-\frac{E(i)}{KT}} \left ( 1-e^{-\frac{E(j)-E(i)}{KT}} \right ) \end{align*} \]因为 \(E(i)<E(j)\),可以推出\(0<e^{-\frac{E(j)-E(i)}{KT}}<1\),于是有 \(P_i(T)-P_j(T) >0\),即 \(P_i(T)>P_j(T)\)
结论:在任何温度 \(T\) 下,系统处于低内能的状态的概率大于处于高内能的状态的概率。
高温下的情况
\[\begin{align*} \lim_{T\to \infty}P_i(T) &= \lim_{T\to \infty} \left[ \frac{e^{-\frac{E(i)}{KT}}}{\sum\limits_{j\in S}e^{-\frac{E(j)}{KT}}} \right ] \\ &= \frac{1}{|S|} \end{align*} \] 其中 \(|S|\) 表示系统所有可能的状态数。
结论:当温度趋近于无穷大时,系统处于各个状态的概率相等,处于均匀分布,与所处状态的内能无关。
低温下的情况
\[\begin{align*} \lim_{T\to 0}P_i(T) &= \lim_{T\to 0} \left[ \frac{e^{-\frac{E(i)}{KT}}}{\sum\limits_{j\in S}e^{-\frac{E(j)}{KT}}} \right] = \lim_{T\to 0} \left[ \frac{e^{-\frac{E(i)-E_m}{KT}}}{\sum\limits_{j\in S}e^{-\frac{E(j)-E_m}{KT}}} \right] \\ &= \lim_{T\to 0} \left[ \frac{e^{-\frac{E(i)-E_m}{KT}}}{\sum\limits_{j\in S_m}e^{-\frac{E(j)-E_m}{KT}}+\sum\limits_{j\notin S_m}e^{-\frac{E(j)-E_m}{KT}}} \right] = \lim_{T\to 0} \left[ \frac{e^{-\frac{E(i)-E_m}{KT}}}{\sum\limits_{j\in S_m}e^{-\frac{E(j)-E_m}{KT}}} \right] \\ &= \begin{cases} \frac{1}{|S_m|}, & if \quad i\in S_m \\ 0, & if \quad i \notin S_m \end{cases} \end{align*} \] 其中 \(S_m\) 表示系统最小内能状态的集合,\(E_m\) 表示系统的最小内能。
结论:当温度趋近于绝对0度时,系统以等概率趋近于几个内能最小的状态之一,而系统处于其它状态的概率为0。即系统达到内能最小状态的概率为1。
温度缓慢下降时的情况
\[\begin{align*} \frac{\partial P_i(T)}{\partial T} &= \frac{\partial}{\partial T} \left[ \frac{e^{-\frac{E(i)}{KT}}}{Z_T} \right] \\ &= \frac{P_i(T)}{KT^2}[E(i)-\overline{E_T}] \begin{cases} >0 \quad if \ E(i)>\overline{E_T}, \quad 高能状态 \\ <0 \quad if \ E(i)<\overline{E_T}, \quad 低能状态 \end{cases} \end{align*} \] 其中 \(\overline{E_T}=\sum\limits_{j\in S}E(j)P_j(T)\) 为状态内能的平均值。
结论:系统处于低能状态的概率随着温度的下降单调上升,而系统处于高能状态的概率随着温度的下降单调下降。
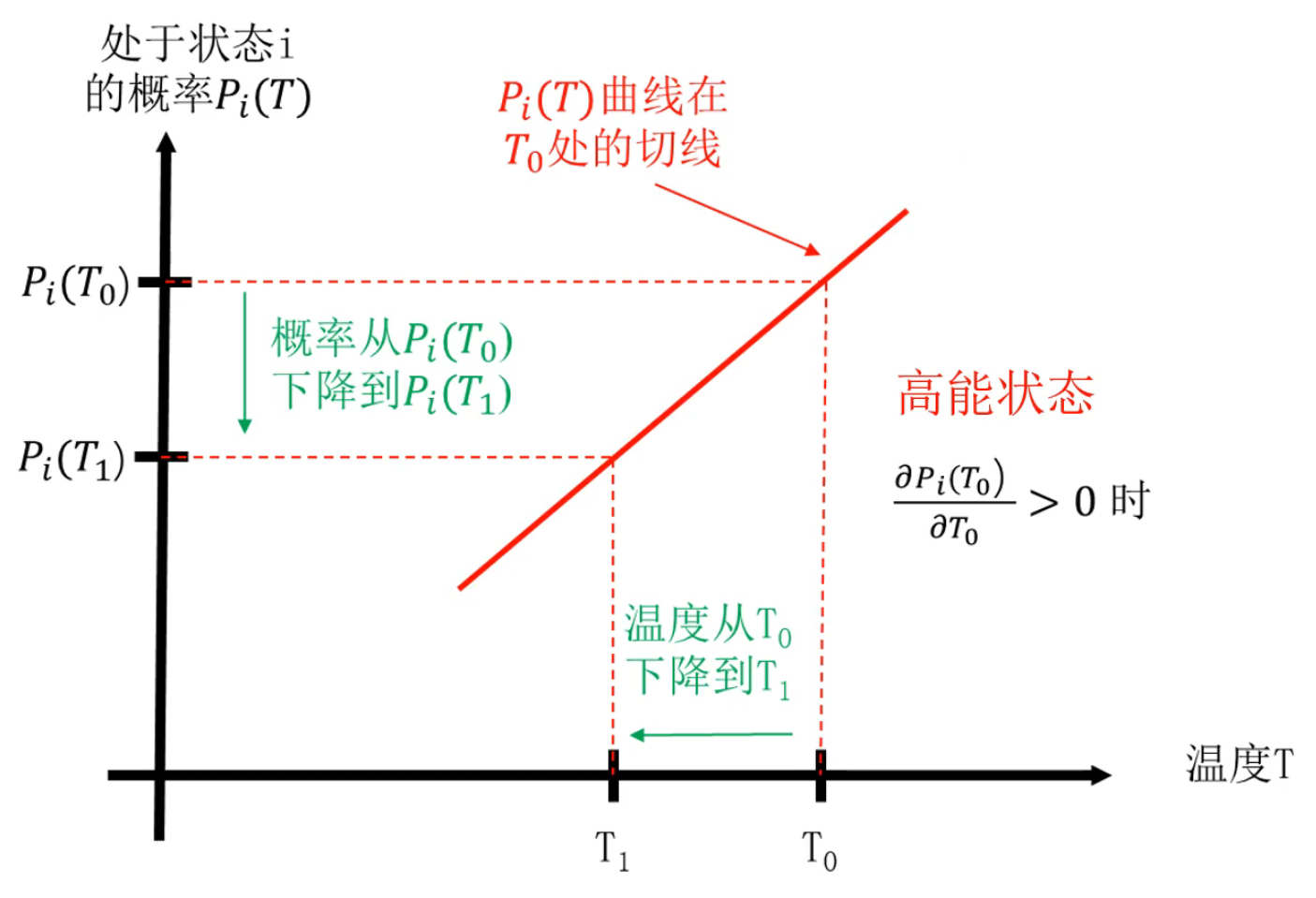
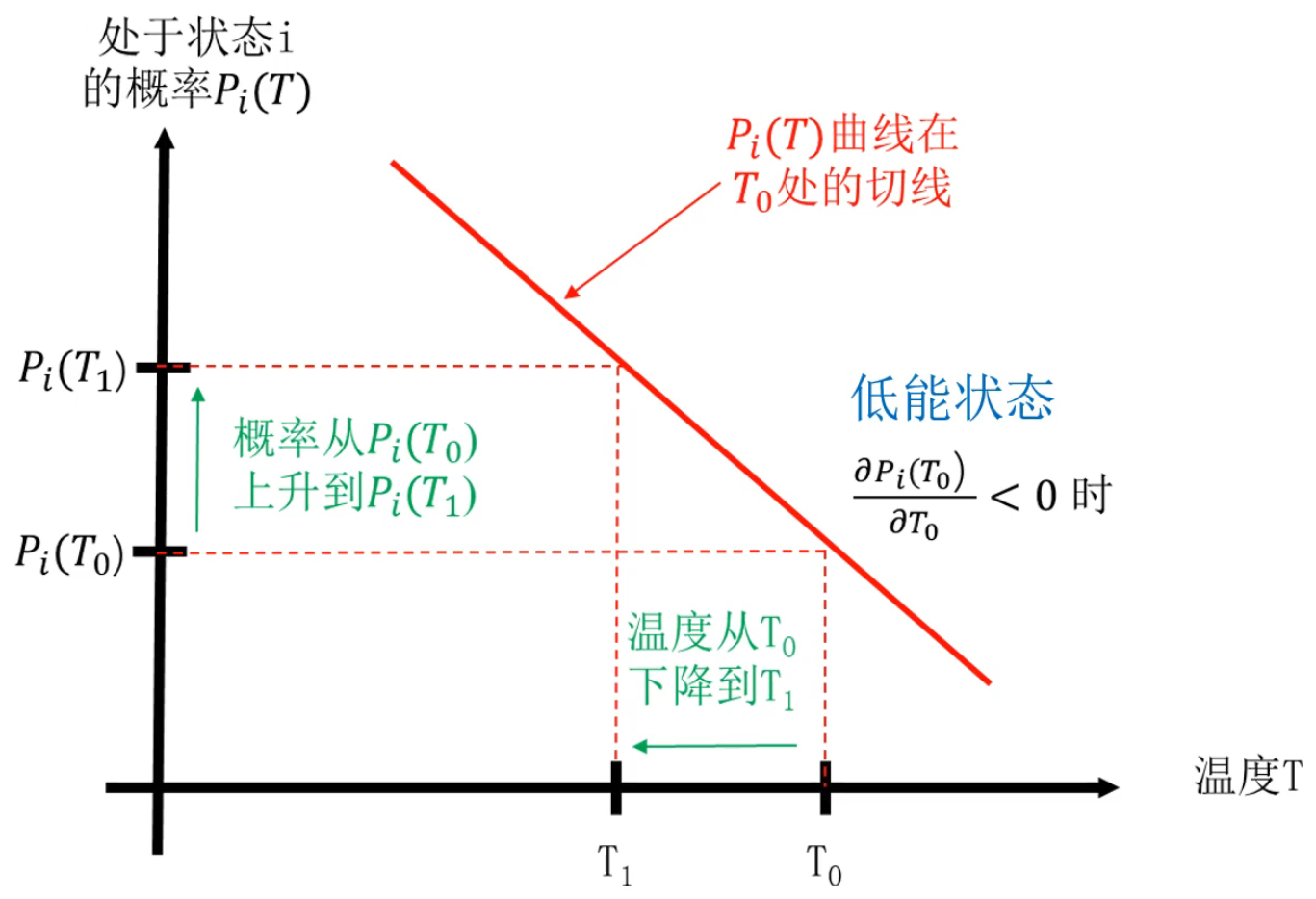
分析:
- 随着温度的缓慢下降,由于处于低能状态的概率越来越大,处于高能状态的概率越来越小,导致状态的内能平均值 \(\overline{E_T}\) 随温度下降而下降,从而使得更多的状态属于高能状态,越来越少的状态属于低能状态。最终,当温度降低到趋近于绝对0度时,只有具有最小内能的状态才属于低能状态。
- 这也从另一个角度说明了当温度趋近于绝对0度时,为什么系统处于最小内能状态的概率为1,这与我们前面的分析是一致的。
退火过程总结
-
在温度不变时,处于低内能状态的概率大于处于高内能状态的概率;
-
当温度趋于无穷大时,系统等概率处于各个状态;
-
当温度趋于绝对0度时,系统达到内能最小状态的概率为1;
-
当温度缓慢下降时,系统处于低能状态的概率随着温度的下降单调上升,而系统处于高能状态的概率随着温度的下降单调下降。
-
退火过程的三个条件:
- 初始温度必须足够高;
- 在每个温度下状态的交换必须足够充分;
- 温度 \(T\) 的下降必须足够缓慢。
退火过程的两点启示
- Metropolis准则
- 如果 \(E(j)\le E(i)\),则状态转换被接受;
- 如果 \(E(j)>E(i)\),则状态转移被接受的概率为:\(e^{\frac{E(i)-E(j)}{KT}}\)
其中 \(i\) 是旧状态,\(j\) 是新状态。
- 当温度缓慢趋于绝对0度时,系统以概率1达到内能最小状态。