完全信息动态博弈中信息是完全的,即双方都掌握参与者对他参与人的策略空间和策略组合下的支付函数有完全的了解,但行动是有先后顺序的,后动者可以观察到前者的行动,了解前者行动的所有信息,而且一般都会持续一个较长时期。
一、扩展式博弈(博弈树)

参与人集合N
策略集A:表示所有可能的策略。不过在一些结点上可能只有一部分可以选择的策略。
历史集H:“策略的序列”构成的集合,可以是有限集或者无限集。H中的元素称为历史(history)。性质:
(1)\(\emptyset\in H\),表示博弈树的根结点。
(2)如果策略序列\(a^1a^2\dots a^k \in H\)且\(s<k\),那么\(a^1a^2\dots a^s \in H\)
(3)每一条历史序列都对应博弈树的一个结点,对应历史序列末端到达的结点。
(4)在完全信息扩展式博弈中,历史集大小=结点个数。
(5)最终历史(Terminal history):如果\(a^1a^2\dots a^k \in H\),但\(a^1 a^2 \dots a^{k+1} \notin H,for any\quad a^{k+1}\in A\)
(6)最终历史集(Terminal history set):Z = {All Terminal history},在这些结点上是收益。
博弈玩家函数(Player Function)P:
(1)\(P :H \backslash Z \rightarrow N\),给每一个非终结历史分配玩家集N中的一个元素。
(2)\(P(h)\)表示在历史h后,轮到哪个玩家做决策。
收益函数(Payoff Function)\(u_i:Z \rightarrow R\),表示第\(i\)个玩家的收益。
扩展式博弈\(G=\{N, H, P,\{u_{i}\}\}\)(不需要策略集A,用上面四个就可以完全刻画一个扩展式博弈,因为策略都包含在历史里了)
例1:最后通牒博弈

由博弈树转化为扩展式博弈:
\(G=\{N, H, P,\{u_{i}\}\}\)
\(N = \{A,B\}\)
\(H=\{∅,(2.0),(1,1),(0,2),((2,0,y)),((2,0),n),((1,1),y),((1,1),n),((0,2),y),((0,2),n)\}\)
\(P: P(\emptyset)=A ; P((2,0))=B ; P((1,1))=B ; P((0,2))=B\)
\(
\begin{array}{l} u_{1}((2,0), y)=2, u_{1}((2,0), n)=0,\\ u\_{1}((1,1), y)=1, u_{1}((1,1), n)=0,\\ u_{1}((0,2), y)=0, u_{1}((0,2), n)=0, \\ u_{2}((2,0), y)=0, u_{2}((2,0), n)=0, \\u_{2}((1,1), y)=1, u_{2}((1,1), n)=0, \\ u_{2}((0,2), y)=2, u_{2}((0,2), n)=0 \end{array}\)
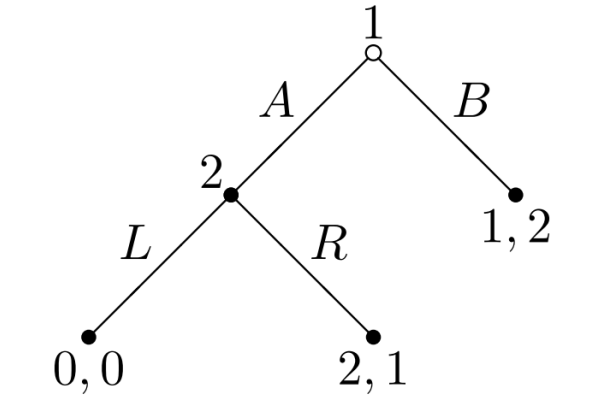
例2:由扩展式博弈定义画出博弈树
\(\begin{array}{l} G=\{N, H, P,t\{u_{i}\}\} \\ N=\{1,2\} \\ H=\{\emptyset, A, B, A L, A R\} \\ P: P(\emptyset)=1 ; P(A)=2 \\ u_{1}(B)=1, u_{1}(A L)=0, u_{1}(A R)=2 \\ u_{2}(B)=2, u_{2}(A L)=0, u_{2}(A R)=1 \end{array}\)
画出博弈树:
二、子博弈完美均衡(SPE)——逆向递推法
从最末端的非叶子结点开始(从最后的子博弈开始),计算NE(此时对于这个非叶子结点的玩家,相当于寻找他的最优收益)。用这个收益,替代这个子博弈根结点。重复直到根节点。通过逆向归纳构造的策略博弈集等价于SPE的集合
例1:唯一的SPE

红色的勾表示选择这个分支。从下往上推,每个人选择自己收益较高的分支。
例2:不唯一的SPE
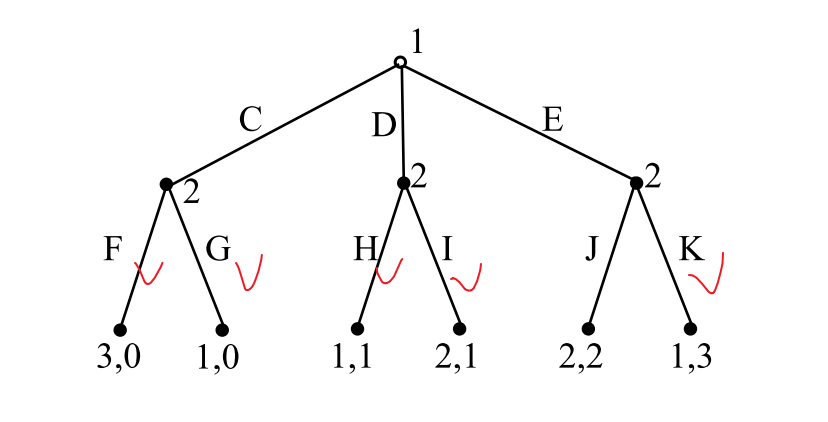
在最高收益相等的时候,根据纳什均衡的定义,这些收益最高的都是纳什均衡。玩家2会选择的纯策略可能有4种:FHK、FIK、GHK、GIK。当玩家2选择FHK的时候,玩家1在三个分支上的收益分别是:3, 1, 1。因此,玩家1会选择C,得到一个SPE:(C, FHK)。同理得到所有的SPE:(C, FHK)、(C, FIK)、(C, GHK)、(D, GHK)、(E, GHK)、(D, GIK)。
例3:三回合议价博弈
甲乙分1万元,博弈规则: (1) 甲先提方案,乙接受则议价结束,拒绝则由乙提方案;(2)若甲接受,议价结束,拒绝则由甲提新方案,乙必须接受;(3) 议价每多进行一回合,双方分得现金产生消耗,消耗系数为δ(eg:0.98)

根据逆推归纳:第三回合是确定的。从第二回合开始,乙的最优策略,使甲的收益不低于\(\delta^2 S\),即\(\delta S_2= \delta^2 S\),所以$S_2=\delta S $,同时要使 \(\delta(10000-S_2)\geq\delta^2(10000-S)\),显然成立。
第一回合时甲知道乙的策略,所以给乙$ \delta(10000-S_2)$,即 \(\delta(10000-\delta S)\),甲剩余\(10000(1-\delta)+\delta^2S\)
对于子博弈纳什均衡进一步分析:第三回合甲的方案乙必须接受\(S=10000\),所以甲得益\(\mathbf{S}_1=10000(1-\delta+\delta^2)\),最终:
\[[10000(1-\delta+\delta^2),10000(\delta-\delta^2)] \]① δ—越接近1,甲接近得到全部得益,乙的得益接近0;
② δ—越接近0,甲接近得到全部利益,乙的得益接近0;
③ δ = 0.5,甲得到7500元,乙可分得最多的2500元, δ=0.5 给乙带来的议价能力最大。
甲具有优势的原因 : A. 先行优势; B. 结束博弈的特权
例4:强盗分金
有5个强盗抢得10枚硬币,在如何分赃上争论不休,于是他们决定:(1)抽签决定个人的号码(1,2,3,4,5);(2)由1号提出分配方案,然后5人表决,如果方案超过半数同于就通过,否则他被扔进大海喂鲨鱼;(3)1号死后,2号提方案,4人表决,当且仅当超过半数同意时方案通过,否则2号被扔进大海;(4)依次类推,知道找到一个每个人都接受的方案(当然,如果只剩5号,他独吞),结果会如何?
很多人认为抽到1号签的海盗很不幸,因为他们很难活下去。但实际上,只要他的分配方案能让至少两个海盗同意,他就可以活下去。那么1号海盗应该怎么做呢?他需要分析自己所处的境况,笼络两个处于劣势的海盗同意他的方案。倒推法可以帮助我们解决这个问题。我们应该从4号和5号两个海盗入手,以此作为问题的突破口。对于5号海盗来说,前面4个海盗全部扔进海里是最好的,自己独吞100枚金币。但这种看似最有利的形势,对于5号海盗来说,却未必可行。因为在只剩下他和4号海盗的时候,4号海盗一定会提出100:0的分配方案,这个方案一定能获得通过。
当3号、4号、5号海盗存在时,金币的分配方案是99:0:1。3号提出99:0:1的方案,自己得到99枚金币,4号得到0枚金币,5号得到1枚金币。3号会同意,4号会反对,而5号会赞同,因为否则,接下来只剩下5号和4号,5号一个都得不到,所以金币分配方案变成了99:0:1。当2号、3号、4号、5号共存时,2号海盗的最好方案是笼络5号海盗,放弃3号海盗和4号海盗,分配方案为98:0:0:2。5号会同意,而3号和4号会反对。2:2通过,金币分配方案为98:0:0:2。
当1号到5号都在时,1号提出方案为98:0:1:1:0,3号、4号和1号会同意,而2号和5号反对也不影响方案通过。所以,结果就是1号得到98枚金币,3号得到1枚金币,4号得到1枚金币,2号和5号一枚金币也得不到。
例5:委托——代理理论
委托代理人关系的一个问题是代理人工作成果的确定性问题,即代理人的工作成果是否完全由其工作情况所确定。代理人的工作成果取决于努力程度,无意外风险导致工作成果减少。委托人可根据工作成果掌握代理人的工作情况。
三阶段委托代理:
① 代理人努力时双方得益 R(E):委托人的较高收益 ;w(E):代理人的较高报酬;E:代理人努力工作的成本
② 代理人偷懒时双方得益 R(S):委托人的较低收益 ;w(S):代理人的较低报酬; S:代理人偷懒工作的成本

采用逆推归纳法:第三阶段:必须满足w(E)-E>w(S)-S ,代理人才会选择努力,这一约束称为激励相容约束。经济意义:只有当代理人得到的报酬,在其偷懒所得报酬的基础上有一个补偿,代理人才选择努力。第二阶段:代理人参与委托的条件: $$w(E)-E>0,w(S)-S>0$$,这称为参与约束。 第一阶段:A. 代理人努力时委托人的选择:\(R(E)-w(E) > R(0)\)——委托,\(R(E)-w(E) < R(0)\)——不委托;B. 代理人偷懒时委托人的选择:\(R(S)-w(S) > R(0)\)——委托,\(R(S)-w(S) < R(0)\)——不委托。
