图论口胡记录
Xor-MST
\(Borvuka\)算法版题
\(Borvuka\)的流程是每次对于每个联通块中都找到一条向外部最小的边,然后再将边相连的两个连通块合并。可以发现每次连通块的个数都会减半,只会合并\(\log_n\)次,那么中间找最小边的过程中,对于没有显式建边的题目我们就可以用数据结构维护求出最小边。总时间复杂度为\(O(n\log_n\times DS)\)。
对于这道题,我们考虑用\(0-1trie\)快速计算异或最小值。记合并过程中同一个连通块的点同色,那么可以先将所有节点值加入\(trie\)中,当找某个连通块向外的最小边时就将\(trie\)中所有该种颜色的点删除查最值,然后再插回去即可。复杂度\(O(n log_n^2)\)。
ll boruvka(){
dsu.init(n);
for (int i=1;i<=n;i++){
col[i]=i;
t.insert(a[i],1,i);
}
cnt=0;ans=0;
while(cnt<n-1){
for (int i=1;i<=n;i++) v[i].clear();
for (int i=1;i<=n;i++){
v[col[i]].push_back(i);
}
for (int i=1;i<=n;i++){
if (v[i].size()){
mn[i]=0x3f3f3f3f;
for (const auto &x:v[i]) t.insert(a[x],-1,x);
for (const auto &x:v[i]){
pair <int,int> p=t.query(a[x]);
if (p.first<mn[i]){
out[i]=make_pair(x,p.second);
mn[i]=p.first;
}
}
for (const auto &x:v[i]) t.insert(a[x],1,x);
}
}
for (int i=1;i<=n;i++){
if (v[i].size()){
int u=out[i].first,v=out[i].second;
int X=dsu.find(u),Y=dsu.find(v);
if (X==Y) continue;
if (dsu.siz[X]>dsu.siz[Y]) swap(X,Y);
cnt++;ans+=a[u]^a[v];
dsu.fa[X]=Y;dsu.siz[Y]+=dsu.siz[X];
}
}
for (int i=1;i<=n;i++) col[i]=dsu.find(i);
}
return ans;
}
Tree MST这道题也可以用\(Brovuka\)做。
P3645 [APIO2015] 雅加达的摩天楼
有一个很明显的暴力:对于每个节点每次向左/右跳到达的点连边,跑一遍\(b_0-b_1\)的最短路就是答案。
考虑优化这个算法,可以想到每个点只向\(b_i-p_i\),\(b_i+p_i\)连边。然而无法保证正确性,因为中间办法更换\(doge\),只能建n张子图,每个点都向左右\(i\)的位置连边,空间时间都吃不消。
又因为类比弹飞绵羊当步长比较大时,暴力跳复杂度是正确的,所以考虑根号分治。设分治阀域为\(len\),建出\(1-len\)的子图。对于\(p_i\)大于\(len\)的点直接暴力连边,小于\(len\)的点将其与\(p_i\)的子图上对应节点连边再跑最短路即可。
for (int i=1;i<=len;i++){
for (int j=1;j<=n;j++){
if (j-i>=1) add(n+(i-1)*n+j,n+(i-1)*n+j-i,1);
if (j+i<=n) add(n+(i-1)*n+j,n+(i-1)*n+j+i,1);
add(n+(i-1)*n+j,j,0);
}
}
for (int i=1;i<=n;i++){
for (const auto &x:vec[i]){
if (p[x]>len){
for (int j=i-p[x],stp=1;j>=1;j-=p[x],stp++) add(i,j,stp);
for (int j=i+p[x],stp=1;j<=n;j+=p[x],stp++) add(i,j,stp);
}
else add(i,n+(p[x]-1)*n+i,0);
}
}
分析\(len\)取何值时复杂度最优,子图会建\(3*len*n\)条边,暴力会连\(\frac{n^2}{len}\)条边,由均值有当\(len\)取\(\sqrt{\frac{n}{3}}\)时最优。
Dynamic Shortest Path
每次暴力更新后重新跑最短路复杂度\(O(qnlogm)\)比较接近时间限制,考虑优化使得每次不重跑最短路将\(log\)优化掉。
首先第一次\(dij\)跑出最短路后,先暴力将每条更新边加一,再记录下每个点最短路的改变量\(delta_i\),显然有\(delta_i<=min(n-1,v)\),因此考虑类似于最短路的松弛操作,开\(min(n-1,v)\)个\(queue\)记录\(delta_i\),每次取出一个节点\(x\),用\(dis[x]-dis[y]+w'+delta[x]\)(即当前节点改变量和前驱传过来的变化量之和)最小值尝试更新邻接点\(delta\)。最后再将每个节点\(dis\)加上\(delta_i\)即可。
for (int i=1;i<=n;i++) delta[i]=1e9;
for (int i=1;i<=v;i++){
int x;read(x);
E[x].w++;
}
delta[1]=0;vec[0].push(1);
for (int i=0;i<=min(n-1,v);i++){
while(vec[i].size()){
int x=vec[i].front();vec[i].pop();
if (delta[x]!=i) continue;
for (int j=head[x];j;j=E[j].nxt){
int y=E[j].to,w=E[j].w;
int tmp=w+dis[x]-dis[y]+delta[x];
if (tmp<delta[y]&&tmp<=min(n-1,v)){
delta[y]=tmp;
vec[tmp].push(y);
}
}
}
}
for (int i=1;i<=n;i++){
if (delta[i]!=1e9) dis[i]+=delta[i];
}
CF1473E Minimum Path
妙妙题。
有一个比较显然的暴力是对于每个节点都用\(m^2\)个状态,即设\(dis(u,l,r)\)为在\(u\)点进过边权最小为\(l\),最大为\(r\)时的最短路,直接跑\(dij\)。
但是这样会有很多冗余的状态,考虑优化。先思考一个弱化的问题:求免费和加倍的边权在这条路径上任意分别取一条的最短路。显然这两条边一定分别是最大边和最小边,因此这个问题和原问题是等价的,这就是这道题比较神仙的思想。
那么接下来考虑对等价问题设计优化的状态,设\(dis(u,0/1,0/1)\)为到\(u\)且最大/最小边选/未选的最短路长度。讨论同状态之间和从0变为1的转移即可,比较简单,不再赘述。这玩意的本质是拆点。
注意最后的答案是\(min(dis[i][1][1],dis[i][0][0])\) (因为可能有只走一条边的情况,但是在等价问题中这条边会被选两次)
跳蚤王国的宰相
首先可以求出原树的重心\(C\)。
考虑对于每个不为\(C\)的节点\(x\)计算答案,发现从\(x->C\)的路径是这样的。
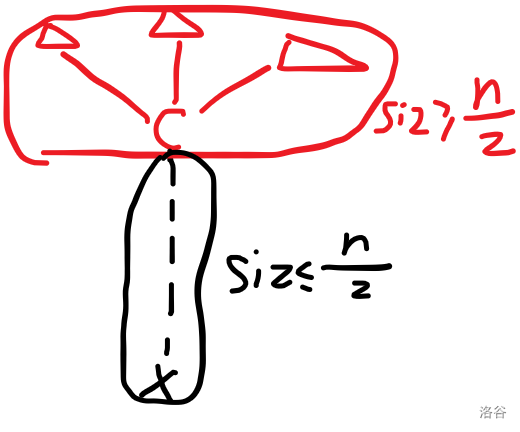
由于\(C\)是重心,所以\(x\)子树一定大小之和小于\(n/2\),只需要考虑将图中的一部分边断开接到\(x\)下边。
显然这样的边不可能在\(x->C\)的路径上,因为C子树大小大于等于\(n/2\),因此只能在\(C\)子树内。
考虑将\(C\)所有儿子按子树大小排序,每次贪心地选取子树大小最大,正确性显然。
然后讨论割完后\(x->C\)的路径节点数+\(C\)剩余子树大小\(\leq\) \(n/2\)已经满足条件,和\(C\)剩余子树大小\(\leq\) \(n/2\)后再多割一刀将\(C\)整棵子树割下来到\(x\)上两种情况。
实现上前缀和加二分即可。
for (int i=1;i<=n;i++){
if (i==rt){puts("0");continue;}
int s=n-siz[bel[i]],delta=s-n/2;
if (delta==0) {puts("0");continue;}
int L=0,R=(int)vec.size()-1,p=-1,P;
while(L<=R){
int mid=(L+R)>>1;
int cur=sum[mid];
if (mid>=pos[bel[i]]) cur-=siz[bel[i]];
if (n-siz[i]-cur<=n/2) P=mid,p=mid,R=mid-1;
else if (s-cur<=n/2) P=mid,p=mid+1,R=mid-1;
else L=mid+1;
}
if (P>=pos[bel[i]]) p--;
printf("%d\n",p+1);
}