0.前言
题目传送门:here
1.概念
网络是什么?一张带权的图
网络最大流是什么?
举个例子
-
想象一些有向的水管,每个水管都有固定的流量上限,有源点可以出水,
有汇点可以收水,问汇点单位时间最多可收到多少水。 -
有很多人要坐火车从起点站要到终点站 每个站的票数是确定的 乘客经过一个站就要买票 最后有多少个乘客能到终点?
这些问题就是网络最大流
2.算法求解
1.Ford–Fulkerson
首先给出如下定义:
- 反向边 如果有一条从节点\(u\)到节点\(v\)流量为\(w\)的边,那么加入一条反向从\(v\)到\(u\)流量为0的边
为什么要搞反向边?
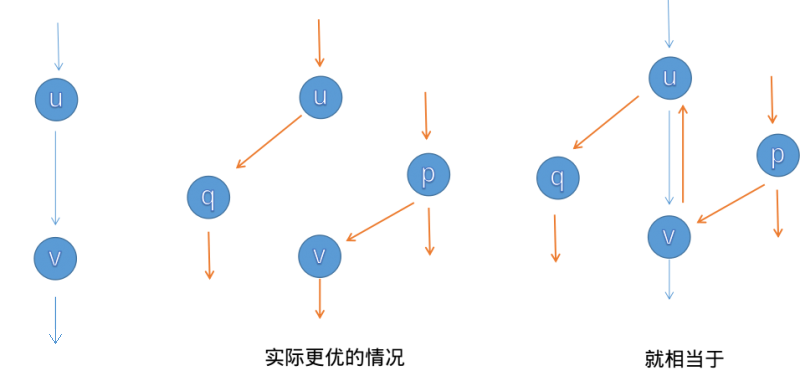
如图,我们可以通过反向边来反悔我们之前的操作 因为每次都贪心地去找S到T的路线不一定是最优的 很可能出现遗漏 因此需要用反向边通过反悔来解决这个问题
怎么反悔呢?如果一条路线\(u\)到\(v\)流量少了\(w\) 那么需要在反向边加上\(w\)即可
给出如下定义
- 找出残量网络 r 中从 S 到 T 的一条路径,其中 r 的值都大于 0,
称为一条增广路。 - 取其中 r 的最小值 x,并为增广路上的每条边流 x 的流量,这一
调整过程叫增广。
什么时候有最大流呢?就是增广到没有增广路为止
所以第一个算法就出来了:
每次\(DFS\)找增广路,找到就增广
我们就得到了这个时间复杂度为\(O(m*\)最大流量\()\)的辣鸡算法 妥妥T
所以我们要学习更加优秀的算法
2.Edmonds–Karp
只考虑容量为正的边,并改用 \(BFS\) 找增广路。
- 最短路单调定理:在 EK 算法不断增广的过程中,源点到各个点的最短路单调不降。
证明自己去查吧 我不会证
这个算法和上面的真没什么变化 就是把 \(DFS\)变成\(BFS\)
Code
#include<bits/stdc++.h>
#define M 5005
#define ll long long
using namespace std;
int n,m,s,t;
int head[205],tot=2;
int vis[205],from[205];
ll minn[205],ans;
queue<int>q;
struct edge{
int to,next;
ll w;
}e[M*2];
void add(int u,int v,int w)
{
e[tot]=(edge){v,head[u],w};
head[u]=tot++;
}
int bfs()
{
fill(vis+1,vis+1+n,0);
q.push(s);
vis[s]=1;
minn[s]=1e9;
while(!q.empty())
{
int x=q.front();
q.pop();
for(int i=head[x];i;i=e[i].next)
{
if(e[i].w==0) continue;
int to=e[i].to;
ll w=e[i].w;
if(vis[to]) continue;
minn[to]=min(minn[x],w);
from[to]=i;
vis[to]=1;
q.push(to);
}
}
return vis[t];
}
void updata()
{
int x=t;
while(x!=s)
{
int i=from[x];
e[i].w-=minn[t];
e[i^1].w+=minn[t];
x=e[i^1].to;
}
ans+=minn[t];
}
int main()
{
scanf("%d%d%d%d",&n,&m,&s,&t);
for(int i=1;i<=m;i++)
{
int u,v;
ll w;
scanf("%d%d%lld",&u,&v,&w);
add(u,v,w);
add(v,u,0);
}
while(bfs()) updata();
printf("%lld",ans);
return 0;
}
代码里有个妙点
e[i].w-=minn[t];
e[i^1].w+=minn[t];
x=e[i^1].to;
这段代码是将从\(T\)到\(S\)当前增广路径上的所有边减去增广的值 反向边加上增广的值
因为tot从2开始 所以每对边的编号为\([2,3],[4,5],[6,7]…\) 容易发现正反边的关系就是异或1
为什么改个\(BFS\)时间复杂度就变了呢?
首先,一次\(BFS\)时间复杂度为\(O(m)\)
根据最短路单调定理 最短路长度单调递增 最多\(O(n)\)种
每种最短路有\(O(m)\)种情况
总时间复杂度是\(O(nm^2)\)
可是这个算法稠密图还是会T啊 于是还是要学习更优秀的算法
3.Dinic
这是\(EK\)算法的优化版
优化:一次性处理完\(S\)到\(T\)最短路保持不变时的所有情况
算法步骤:
- 1.先\(BFS\)求出每个点距离\(S\)的最短距离
- 2.然后\(DFS\)求出到每个点的流量
优化:
- 1.当前弧优化:如果当前流到了第x条边,且前x条边流满了,下一次直接从第x+1条边开始流就行了(不加时间复杂度退化成\(EK\)算法)
- 2.不完全BFS优化:遍历到了\(T\)整个\(BFS\)就可以退出了
- 3.点优化:多路增广时,若从某个点出发流不出流量,直接将其从最短路
DAG 中剔除
这样时间复杂度就能优化成\(O(n^2m)\)了
Code
#include<bits/stdc++.h>
#define MAXN 205
#define ll long long
using namespace std;
int n,m,s,t;
int tot=2,head[MAXN];
int dis[MAXN],pre[MAXN];
int q[MAXN],l,r;
ll ans;
struct edge{
int to,next,w;
}e[10005];
void add(int u,int v,int w)
{
e[tot]=(edge){v,head[u],w};
head[u]=tot++;
}
bool bfs()
{
fill(dis,dis+1+n,-1);
l=r=0;
q[++r]=s;
dis[s]=0;
pre[s]=head[s];
while(l<r)
{
int x=q[++l];
for(int i=head[x];i;i=e[i].next)
{
int to=e[i].to;
if(e[i].w>0&&dis[to]==-1)
{
dis[to]=dis[x]+1;
q[++r]=to;
pre[to]=head[to];
dis[to]=dis[x]+1;
if(to==t) return 1;
}
}
}
return 0;
}
int dfs(int x,ll sum)
{
if(x==t) return sum;
ll k,cnt=0;
for(int i=pre[x];i&∑i=e[i].next)
{
pre[x]=i;
int to=e[i].to;
if(e[i].w>0&&dis[to]==dis[x]+1)
{
k=dfs(to,min(sum,1ll*e[i].w));
if(k==0) dis[to]=1e9;
e[i].w-=k;
e[i^1].w+=k;
cnt+=k;
sum-=k;
}
}
return cnt;
}
int main()
{
scanf("%d%d%d%d",&n,&m,&s,&t);
for(int i=1;i<=m;i++)
{
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
add(v,u,0);
}
while(bfs()) ans+=dfs(s,1e9);
printf("%lld",ans);
return 0;
}
费用流
链接:cilck
现在自来水厂要收费了,每个水管流过都要给钱 求能得到最多水的同时钱最少
其实这个问题十分简单 我们建边时把输入边花费设为正数,反向边设为负数(反悔)
然后把 bfs 改成 spfa就行了
因为有负权边 所以不能用Dij 需要转化
EK
#include<bits/stdc++.h>
#define MAXN 50005
#define MAXM 500005
#define ll long long
using namespace std;
int n,m,s,t;
int minn[MAXN],vis[MAXN],last[MAXN],dis[MAXN];
int q[MAXN],l,r;
int tot=2,head[MAXN];
int ans1,ans2;
struct edge{
int to,next,w,c;
}e[MAXM*2];
void add(int u,int v,int w,int c)
{
e[tot]=(edge){v,head[u],w,c};
head[u]=tot++;
}
int spfa()
{
fill(dis+1,dis+1+n,2e9);
fill(vis+1,vis+1+n,0);
l=r=0;
dis[s]=0;
vis[s]=1;
minn[s]=2e9;
q[++r]=s;
while(l<r)
{
int x=q[++l];
vis[x]=0;
for(int i=head[x];i;i=e[i].next)
{
int v=e[i].to;
if(e[i].w&&dis[x]+e[i].c<dis[v])
{
dis[v]=dis[x]+e[i].c;
minn[v]=min(minn[x],e[i].w);
last[v]=i;
if(!vis[v])
{
vis[v]=1;
q[++r]=v;
}
}
}
}
return dis[t]!=2e9;
}
void updata()
{
int x=t;
while(x!=s)
{
int i=last[x];
e[i].w-=minn[t];
e[i^1].w+=minn[t];
x=e[i^1].to;
}
ans1+=minn[t];
ans2+=dis[t]*minn[t];
}
int main()
{
scanf("%d%d%d%d",&n,&m,&s,&t);
for(int i=1;i<=m;i++)
{
int u,v,w,c;
scanf("%d%d%d%d",&u,&v,&w,&c);
add(u,v,w,c);
add(v,u,0,-c);
}
while(spfa()) updata();
cout<<ans1<<" "<<ans2;
return 0;
}
二分图匹配
链接:click
什么意思呢? 左边有\(n\)个点,右边\(m\)个点 然后中间有\(e\)条边可以连边
求最终能有多少个点能匹配
思路
转化一下网络流模型就行
设开始点为\(0\)号点 终点为\(n+m+1\)号点 然后0号点向左侧的点连一条流量为1的边,右侧点向终点连一条流量为1的边 最终输出流量即可
记得加大空间
#include<bits/stdc++.h>
#define MAXN 505
#define MAXM 50005
#define ll long long
using namespace std;
int n,m,k,ans;
int s,t;
int pre[MAXN*2],dis[MAXN*2];
int q[MAXN*2],l,r;
int tot=2,head[MAXN*2];
struct edge{
int to,next,w;
}e[MAXM*3];
void add(int u,int v,int w)
{
e[tot]=(edge){v,head[u],w};
head[u]=tot++;
}
int bfs()
{
fill(dis,dis+1+n+m+1,-2);
l=r=0;
q[++r]=s;
pre[s]=head[s];
dis[s]=0;
while(l<r)
{
int x=q[++l];
for(int i=head[x];i;i=e[i].next)
{
int to=e[i].to;
if(e[i].w&&dis[to]==-2)
{
dis[to]=dis[x]+1;
pre[to]=head[to];
q[++r]=to;
if(to==t) return 1;
}
}
}
return 0;
}
int dfs(int x,int sum)
{
if(x==t) return sum;
int t,cnt=0;
for(int i=pre[x];i&∑i=e[i].next)
{
pre[x]=i;
int to=e[i].to;
if(e[i].w&&dis[to]==dis[x]+1)
{
t=dfs(to,min(sum,e[i].w));
if(t==0) dis[to]=1e9;
cnt+=t;
sum-=t;
e[i].w-=t;
e[i^1].w+=t;
}
}
return cnt;
}
int main()
{
scanf("%d%d%d",&n,&m,&k);
s=0,t=n+m+1;
for(int i=1;i<=n;i++)
add(s,i,1),add(i,s,0);
for(int i=1;i<=m;i++)
add(n+i,t,1),add(t,n+i,0);
for(int i=1;i<=k;i++)
{
int u,v;
scanf("%d%d",&u,&v);
if(u>n||v>m) continue;
add(u,v+n,1);
add(v+n,u,0);
}
while(bfs()) ans+=dfs(s,2e9);
cout<<ans;
return 0;
}