二分图相关定理

最长反链：一张有向无环图的最长反链为一个集合 \(S \subseteq V \)，满足对于 \(S\) 中的任意两个不同的点 \(u, v \in S(u \ne v)\)，\(u\) 不能到达 \(v\)，\(v\) 也不能到达 \(u\)，且 \(S\) 的大小尽量大

最小不可重链覆盖：在 DAG 中选出若干条链，经过每个点一次，且链数尽量少

最小点覆盖：选取最少的点，覆盖每条边，也就是说每条边的两个端点至少有一个被选中了

最大独立集：一个集合内的点相互没有连边即为独立集，集合大小最大的独立集为最大独立集

Dilworth 定理：一个偏序集中的最长反链大小，等于其中最小不可重链覆盖大小

构造二分图最大独立集（by 小粉兔）：

首先求出二分图最大匹配，
考虑下图，可以求出它的其中一种最大匹配为 \(\{ \langle 2, D \rangle, \langle 3, E \rangle, \langle 4, A \rangle, \langle 5, C \rangle \}\)，设最大匹配大小为 \(m\)，这里 \(m = 4\)：

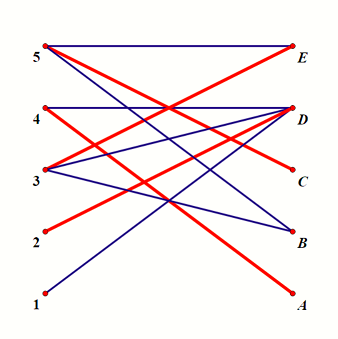
从右侧的非匹配点（这里为 \(B\)，可能有多个）开始 DFS，右侧的点只能走非匹配边向左访问，左侧的点只能走匹配边向右访问：

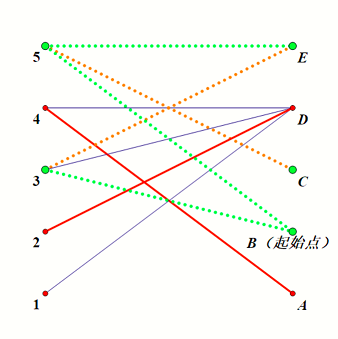
可以发现 DFS 到了 \(3, 5, B, C, E\) 这些点。

我们取左侧被 DFS 到的点，以及右侧没被 DFS 到的点，也就是 \(3, 5, A, D\) 这些点，记做集合 \(S\)，可以证明 \(S\) 是一个最小点覆盖。

证明：

1. 首先有：最小点覆盖等于最大匹配。我们可以证明 \(|S| = m\)
   这是因为：右侧的非匹配点一定都被 DFS 到了，所以在右侧选取的必然是匹配点。如果一个右侧的匹配点没被选取，即它被 DFS 到了，而这只有可能是因为它在左侧匹配到的点被 DFS 到了，那么左侧匹配到的点就会被选上。即是：每条匹配边的两端点恰好会被选一个。而左侧的非匹配点一定不会被 DFS 到，这是因为如果被 DFS 到了，必然会形成一条交错路（匈牙利算法中的），不满足最大匹配的条件。所以有且仅有匹配边的端点会被选上，而且每条匹配边的两端点恰好被选一个，所以 \(\boldsymbol{|S| = m}\)。
2. \(S\) 可以覆盖所有的边。
   我们把边按照左右端点是否被 DFS 到，分成 \(2 \times 2 = 4\) 类。那么如果出现了左端点没被 DFS 到，但是右端点被 DFS 到了的边，它才不会被覆盖。然而这是不可能的，这是因为对于一个右侧被 DFS 到的点，与它相连的左侧的点一定都被 DFS 到了。

然后有最大独立集等于最小点覆盖的补集。也就是只要选出左侧没被 DFS 到的点和右侧被 DFS 到的点就行了。

构造最长反链：

首先求出最小不可重链覆盖大小

可以发现最终答案一定是合并（首尾相接）若干条链形成的。考虑重新描述这个过程：
对于一个点，它在最终的链上，一定只有最多一个前驱，和最多一个后继。
我们考虑把每个点拆成入点和出点，那么入点和出点应该只能匹配上最多一个点（表示前驱或者后继）。

这似乎是二分图匹配的形式，具体地，我们考虑：
把一个点 \(x\) 拆成两个点：\(x_{out}\)​ 和 \(x_{in}\)​，表示出点和入点。
对于一条边 \(x \to y\)，连接 \(x_{out}\)​ 与 \(y_{in}\)​，表示原图中 \(x\) 的出边指向 \(y\)（这条边是 \(y\) 的入边）。
那么最终形成了一个二分图，左侧是所有 \(x_{out}\)，右侧是所有 \(x_{in}\)​。而且所有边都是连接左侧的点和右侧的点的。

在这个二分图 \(G = \langle \langle V_{out}, V_{in} \rangle , E' \rangle\) 上做二分图最大匹配：
每一个匹配边 \(x_{out} \leftrightarrow y_{in}\)​ 都可以还原原图中链的一条边 \(x \to y\)。
每匹配 \(1\) 条边，链的个数就减少 \(1\)，则有最小链覆盖的大小等于 \(n\) 减去最大匹配的大小

继续考虑如何从二分图最大匹配中，构造出最长反链

从上文可以得知如何构造最大独立集，令最大独立集为 \(I\)，考虑选出所有 \(x_{out}\) 和 \(x_{in}\) 都属于 \(I\) 的点，记做集合 \(A\)，它们构成一个最长反链。

证明：
首先有 \(|I| = 2n - |S| = 2n - m\)，而 \(|I| - |A|\) 可以看作是满足「\(x_{out}\) 或 \(x_{in}\) 属于 \(I\)」的 \(x\) 的个数，显然这样的 \(x\) 不会超过 \(n\) 个，所以 \(|I| - |A| \le n\)，所以 \(|A| \ge |I| - n = n - m\)。
由 Dilworth 定理可知 \(|A| = n - m\)，也就是一个最长反链。

总结：只要选出 \(x_{out}\) 没被 DFS 到，且 \(x_{in}\) 被 DFS 到了的点，这些点就组成一个最长反链。