P3243 菜肴制作
题意给出由n个节点组成的有向(不一定无环)图,给出m组限制 (i,j) 代表i节点必须先于j被访问,现询问在满足所有限制的情况下,访问顺序字典序最小的一种
首先考虑 Impossible 的情况:当图出现环的时候产生矛盾,所以只要判定有没有环就好了
思路
一开始用了dfs:反向建边,从小到大遍历寻找每个点,如果目前仍有先于它的菜,继续递归至无前置节点,回溯时输出
数组记录节点出现次数,如果次数小于n个,则说明有环,输出 Impossible
但很快发现反例
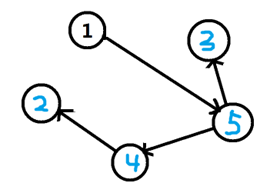
(5,1)(2,4)(4,5)(3,5)
在这个例子里,dfs得到结果为 3 2 4 5 1, 但正确结果应该为 2 3 4 5 1
深搜只能在同一层进行决策,无法看到下一层的更优值
又看了一遍题,发现是拓扑排序
于是写了一遍拓扑交了,结果WA 9个
发现题很坑,要求序号较小的尽量在前,但不一定在前,就像上面的例子
但小的尽量在前,无论是否向前,大编号一定向后,把大编号向后放一定更优
所以想到了解法 (但还是没调出来 :
仍然反向建边,顺序后指向顺序前,在反向图上跑拓扑排序,这样求得的序列一定字典序最大
数组记录序列,最后倒序输出
-
Impossible! :拓扑过程中记录节点出现次数,次数小于n,说明存在环,不成立
-
队列的选取 :因为在寻找过程中要不断找到最大值,所以用优先队列,priority_queue,队首为最大值
(看了看题解,发现少了一行初始化
#include <iostream>
#include <cstdio>
#include <vector>
#include <cstring>
#include <queue>
using namespace std;
const int N = 100009;
int t, m, n, x, y, in[N], ans[N], cnt;
vector<int> v[N]; // 建图
priority_queue<int> q; //大顶堆
inline void TopoSort() {
for (int i = 1; i <= n; i ++)
if (!in[i])
q.push(i);
cnt = 0;
while (!q.empty()) {
int h = q.top();
q.pop();
ans[++ cnt] = h; // 记录出队序列及元素个数
for (int i = 0; i < v[h].size(); i ++) {
int l = v[h][i];
in[l] --;
if (!in[l])
q.push(l);
}
}
}
inline void clear() {
for (int i = 1; i <= n; i ++)
v[i].clear();
memset(in, 0, sizeof in);
memset(ans, 0, sizeof ans);
}
int main() {
scanf("%d", &t);
while (t --) {
scanf("%d%d", &n, &m);
clear(); // 需要初始化
while (m --) {
scanf("%d%d", &x, &y);
v[y].push_back(x); // 反向建边
in[x] ++; // 记录入度
}
TopoSort(); // 拓扑排序
if (cnt < n)
cout << "Impossible!"; // 如果出现节点个数小于 n
else
for (int i = n; i >= 1; i --)
cout << ans[i] << " "; // 倒序输出
cout << endl;
}
return 0;
}