[JOI 2020 Final] 火事 题解

标签：emplace 题解 valueType back pos queue 2020 JOI 100

题面

给定一个长为 \(N\) 的序列 \(S_i\)，刚开始为时刻 \(0\)。

定义 \(t\) 时刻第 \(i\) 个数为 \(S_i(t)\)，那么：

\[\left\{ \begin{array}{ll} S_0(t)=0\\S_i(0)=S_i\\S_i(t)=\max\{S_{i-1}(t-1),S_i(t-1)\} \end{array} \right.\]

共有 \(Q\) 个询问，每次询问给出 \(T_j, L_j, R_j\)，求

\[\sum\limits_{k=L_j}^{R_j}S_k(T_j) \]

（\(1 \le N, Q \le 2 \times 10^5\)）

题解

我们可以列出一个 \(N \times (N + 1)\) 的矩阵，其中第一行为初始数据，第 \(i\) 行为第 \(i - 1\) 时刻时数列的状态。

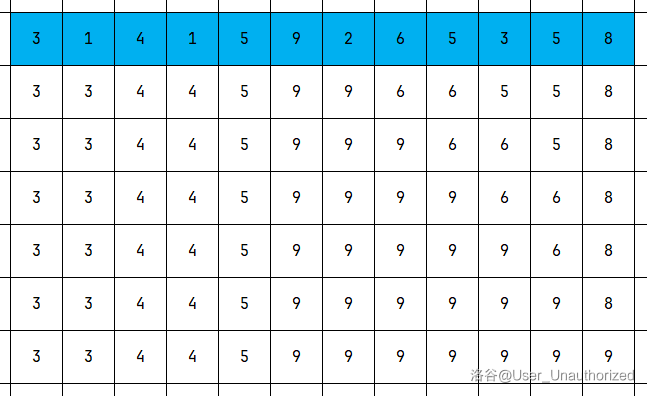
不难看出询问的实质上是一个 \(1 \times M\) 的矩形和，我们可以差分为查询两个前缀和然后相减。

发现题中数列变化的本质是较大数每个时刻均向右覆盖一个较小数，我们把同一个数覆盖的区域用同一种颜色表示，可以得到下图。

可以发现，每个数的贡献区域都可以近似看作一个平行四边形，下面以数 \(6\) 所覆盖的区域为例。

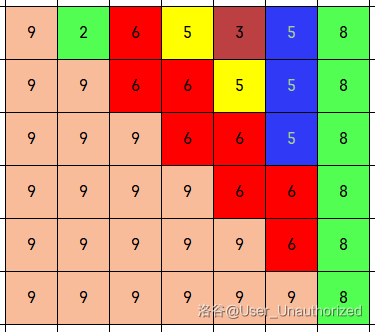
我们可以发现，这个平行四边形的左侧会被一个比他小的数阻挡，而右侧会被一个比他大的数阻挡。

但是我们可以发现，一个平行四边形是很难处理的，于是我们考虑将其拆成三个三角形。

如上图的红色格子构成的平行四边形的和，可以看作一个大三角形与两个小三角形的差。即绿色、红色、蓝色三个颜色构成的大三角形与绿色、蓝色两个小三角形的差。

好的，现在我们已经成功的将平行四边形问题转化为了三角形问题，接下来我们考虑如何处理三角形问题。

我们可以发现这道题中的三角形都是等腰直角三角形，我们考虑将其转化为边平行于坐标轴的矩形，然后用扫描线处理。

我们首先考虑将这个直角三角形的水平右方向全部填充上相同的数，即假设让其产生额外的贡献。

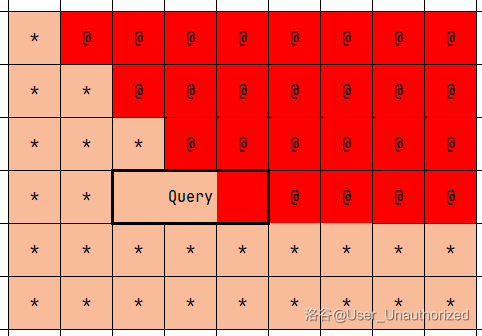
然后我们将这个图形向左倾斜，使其左边界竖直。

注意在这个过程中与图形相关的查询也要同时向左平移。

这个时候我们发现向左移动完成后的图形便是一个矩形，可以利用扫描线求解。

图中的绿的部分不会产生贡献，因为不会有询问对那些格子进行查询，所以无需去除这部分的影响。

图中的蓝色部分在平移之前也是一个矩形，可以利用扫描线求解。

现在我们已经成功的处理了平行四边形，下面我们考虑如何计算贡献。

可以发现，矩形对前缀和的影响是一个有定义域的一次函数，例如上图蓝色部分在 \(x \le 5\) 时不会产生影响，在 \(x > 5\) 时产生的影响呈一次函数关系。根据一次函数的表达式

\[y = ax + b \]

于是我们可以分开处理斜率（\(a\)）和截距（\(b\)），用两个树状数组维护即可。

对于平移之后的图同理，再开两个树状数组维护即可。

我们再回顾一下最开始的图。

我们发现第一个数字 \(3\) 所覆盖的访问貌似不是一个平行四边形，但是我们可以发现其也可以转化为三个三角形。

这就意味着在这道题目中，计算左边第一个比它大的数时对于左边不存在比它大的数要合理的设置边界值。右侧同理。

Code

#include <bits/stdc++.h>

typedef long long valueType;
typedef std::vector<valueType> ValueVector;

constexpr valueType MAX = INT_MAX >> 1;

class TreeArray {
public:
    typedef valueType sizeType;

    static constexpr sizeType shifting = 2e5 + 5;

private:
    sizeType size;

    ValueVector data;

    static valueType lowBit(valueType x) {
        return x & -x;
    }

public:
    explicit TreeArray(sizeType n) : size(n + shifting), data(size, 0) {};

    void insert(sizeType pos, valueType key) {
        pos += shifting;

        while (pos < size) {
            data.at(pos) += key;
            pos += lowBit(pos);
        }
    }

    valueType sum(sizeType pos) const {
        pos += shifting;

        valueType result = 0;

        while (pos > 0) {
            result += data.at(pos);
            pos -= lowBit(pos);
        }

        return result;
    }
};

struct Query {
    valueType id;
    valueType l, r, t;

    Query() : id(-1), l(-1), r(-1), t(-1) {};

    Query(valueType id, valueType l, valueType r, valueType t) : id(id), l(l), r(r), t(t) {};
};

typedef std::vector<Query> QueryVector;
typedef std::pair<valueType, valueType> ValuePair;
typedef std::vector<ValuePair> PairVector;
typedef std::vector<QueryVector> QueryMatrix;
typedef std::vector<PairVector> PairMatrix;

int main() {
    valueType N, Q;

    std::cin >> N >> Q;

    ValueVector source(N + 100), leftBound(N + 100), rightBound(N + 100);

    for (valueType i = 1; i <= N; ++i)
        std::cin >> source.at(i);

    std::deque<ValuePair> queue;

    queue.emplace_back(MAX, -N - 1);

    for (valueType i = 1; i <= N; ++i) {
        while (!queue.empty() && source.at(i) >= queue.back().first)
            queue.pop_back();

        leftBound.at(i) = queue.back().second;

        queue.emplace_back(source.at(i), i);
    }

    queue.clear();
    queue.emplace_back(MAX, N + 1);

    for (valueType i = N; i >= 1; --i) {
        while (!queue.empty() && source.at(i) > queue.back().first)
            queue.pop_back();

        rightBound.at(i) = queue.back().second;

        queue.emplace_back(source.at(i), i);
    }

    TreeArray tree1(N + 100), tree2(N + 100), tree3(N + 100), tree4(N + 100);

    PairMatrix task1(2 * N + 100), task2(2 * N + 100), task3(2 * N + 100), task4(2 * N + 100);

    typedef std::function<void(valueType, valueType, valueType)> addFunction;

    addFunction add = [&](valueType l, valueType r, valueType key) {
        task1.at(0).emplace_back(r, -key);
        task2.at(0).emplace_back(r, (r - 1) * key);
        task3.at(0).emplace_back(l + 1, key);
        task4.at(0).emplace_back(l + 1, -l * key);

        task1.at(r - l).emplace_back(r, key);
        task2.at(r - l).emplace_back(r, -(r - 1) * key);
        task3.at(r - l).emplace_back(l + 1, -key);
        task4.at(r - l).emplace_back(l + 1, l * key);
    };

    typedef std::function<valueType(valueType, valueType)> calcFunction;

    calcFunction calc = [&](valueType x, valueType t) -> valueType {
        return x * tree1.sum(x) + tree2.sum(x) + (x - t) * tree3.sum(x - t) + tree4.sum(x - t);
    };

    for (valueType i = 1; i <= N; ++i) {
        add(leftBound.at(i), i, -source.at(i));
        add(i, rightBound.at(i), -source.at(i));
        add(leftBound.at(i), rightBound.at(i), source.at(i));
    }

    QueryMatrix query(N + 100);
    ValueVector ans(Q);

    for (valueType i = 0; i < Q; ++i) {
        valueType l, r, t;

        std::cin >> t >> l >> r;

        query.at(t).emplace_back(i, l, r, t);
    }

    for (valueType i = 0; i <= N; ++i) {
        for (auto const &iter: task1.at(i)) tree1.insert(iter.first, iter.second);
        for (auto const &iter: task2.at(i)) tree2.insert(iter.first, iter.second);
        for (auto const &iter: task3.at(i)) tree3.insert(iter.first, iter.second);
        for (auto const &iter: task4.at(i)) tree4.insert(iter.first, iter.second);

        for (auto const &iter: query.at(i)) {
            ans.at(iter.id) = calc(iter.r, i) - calc(iter.l - 1, i);
        }
    }

    for (valueType i = 0; i < Q; ++i)
        std::cout << ans.at(i) << '\n';

    std::cout << std::flush;

    fclose(stdin);
    fclose(stdout);

    return 0;
}

标签：emplace,题解,valueType,back,pos,queue,2020,JOI,100
From： https://www.cnblogs.com/User-Unauthorized/p/17593891.html