洛谷-P9485 题解

写在前面：这是蒟蒻交的第一篇绿题题解（大祭），因为线性做法比较难想，本篇会着重讲述用 RMQ 问题求解，并尽可能用清晰明了的图片和简易的文字讲明白。

正文

最坏时间复杂度：\(\mathcal{O}(\sum n+\log \sum n)\)

在求解之前，先让我们想个问题，如何求解积水格数？再简单点，对于每个 \(i\)，其积水高度是多少？看下图。

以 \(i=3\) 为例，我们可以发现，每个 \(i\) 的积水高度与它的左右两峰有关，左边锋（\(i=1\)）高度为 3，是 \([1,3)\) 区间内的最高高度，右边锋（\(i=5\)）高度为 4，是 \((3,5]\) 区间内的最高高度。

大家应该都听过木桶效应吧，\(i=3\) 时积水最多积 2 格，因为再多就会从 \(i=1\) 的位置流出去，所以，积水高度应该是 \(i\) 左右两峰的最小值。

那么，上述问题“对于每个 \(i\)，求其积水高度”已经转化为“对于每个 \(i\)，求其左右峰的高度”，再转化一下：对于每个 \(i\)，求 \([1,i)\) 和 \((i,n]\) 两个区间的最大值。

显然这是可以用 DP 求解的，设 \(l_i\) 为 \(i\) 左边的峰的位置，\(r_i\) 为 \(i\) 右边的峰的位置，\(a_i\) 为 \(i\) 的高度。有如下代码：

l[0]=0,l[1]=0;//求l
for(register int i=2;i<=n;i++)
  if(a[i-1]>=a[l[i-1]]) l[i]=i-1;
  else l[i]=l[i-1];

r[n+1]=0,r[n]=0;//求r
for(register int i=n-1;i>=1;i--)
  if(a[i+1]>=a[r[i+1]]) r[i]=i+1;
  else r[i]=r[i+1];

知道了左右两峰的高度，自然而然也就可以求每个 \(i\) 的积水格数。代码见下，其中 \(p_i\) 为 \(i\) 左右两峰的最小值（也可以理解为 \(i\) 积水最高可达的高度），\(w_i\) 为 \(i\) 的积水格数，\(s\) 为总积水格数。注意特判 \(i\) 自己本身就是峰的情况。

s=0;
for(register int i=1;i<=n;i++){
  p[i]=min(a[l[i]],a[r[i]]);
  if(p[i]-a[i]>0) w[i]=p[i]-a[i];//如果a[i]与左右两峰形成“凹”状
  else w[i]=0;//否则不积水
  s+=w[i];
}

请记住上面的变量符号，后面会用到。

好了，关于积水的问题求解完了，接下来就进入重点了。对于每个 \(i\)，有两种情况：

第一类，\(i\) 存在积水，即 \(p_i>a_i\)。我们对于每个 \(i\)，将 \(a_i\) 增大至 \(p_i\)，即将 \(i\) 升高至积水高度，不能多也不能少，多了可能会形成新的峰，增加积水格数，少了无法排尽 \(i\) 的积水，看下面的图。

此时将 \(a_3\) 提高 2 格，这是恰当好处的，多了的话 \(i=4\) 的积水格数会增加，少了也不最优。

因此，有代码（\(ans\) 是改造后的答案）：

for(register int i=1;i<=n;i++)
  ans=min(ans,s-w[i]);

第二类，\(i\) 是峰。可以尝试降低高度，排出峰内部的积水。这种情况十分复杂，我们要细细研究。

如果我们分别枚举每个 \(i\) 降低高度，再加上判断可以减少多少格积水，时间复杂度就会变成惊人的 \(\mathcal{O}(\sum n_j^2)\)，这是不可接受的，我们要换种思路。（实际上这种思路的时间复杂度没那么夸张，如果数据水还是能过的）

设 \(v_i\) 为将 \(i\) 降低后可以减少的积水格数。枚举每个 \(i\)，分别求其左右峰（\(l_i\) 和 \(r_i\)）降低高度后 \(i\) 可以减少的积水格数，分别将求出的值加在 \(v_{l_i}\) 和 \(v_{r_i}\) 即可。

那么如何求可以减少的积水格数呢？

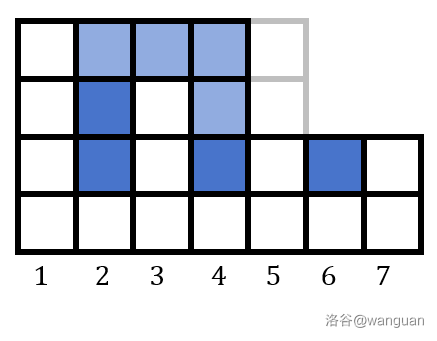
以 \(i=4\) 为例，此时 \(r_i=5\)。如果将 \(a_5\) 降至 0 高度，此时反而会积水（因为此时 \(a_7 > a_5\)，形成“凹”状），所以我们只能将 \(a_5\) 降至 \(a_7\) 的高度，否则会形成多余的积水，那么 \(i=4\) 就可以减少 \(p_4-a_{r_{r_4}}\)。来解释一下，\(r_4\) 是 \(i=4\) 的右峰位置，此时我们要将 \(a_{r_4}\) 降低，但不能低于 \(r_4\) 右边较低峰的位置（图中是 \(i=7\)），即不能低于 \(r_{r_4}\) 的高度，因此 \(a_{r_4}\) 的高度会降至 \(a_{r_{r_4}}\)，所以 \(i=4\) 可以减少 \(p_4-a_{r_{r_4}}\) 格积水。

综上：对于每个 \(i\)，使得 \(v_{r_i}\leftarrow v_{r_i}+(p_i-a_{r_{r_i}})\)。

那么，如果我们这样写，就可以愉快的 WA 了。

来，看看 \(i=2\) 的情况，若按上述想法应减少 2 格积水，但实际上是 1 格，WHY？看看 \(i=3\)，当 \(a_5\) 降至 \(a_7\) 后，它成了 \(i=2\) 的右峰，挡住了 \(i=2\) 的一部分积水，使得其只能减少 1 格。所以还要求 \((i,r_i)\) 区间内的最大值 \(y\)，计算会不会出现新的峰。

这里就是 RMQ 问题了，因为是离线的，可以用 ST 表解决（当然你想用线段树也没人拦你，只是蒟蒻不太会QWQ）。

把上述结论的 \(a_{r_{r_i}}\) 改为 \(\max(a_{r_{r_i}},y)\) 就好了。

但是！！！还没结束！！！看 \(i=3\)，\(a_5\) 降至 \(a_7\) 后，在区间 \([3,7]\) 中 \(a_3\) 是最大的，也就是说 \(i=3\) 减少的积水格数是 \(p_3-a_3\)，不与 \(j\) 或 \(a_{r_{r_i}}\) 有关。

所以还要在 \(\max\) 内加上第三项 \(a_i\)。

这里只讨论了降低右峰的情况，左峰同理。

好啦，上这部分的 Code！

for(register int i=1;i<=n;i++){
  if(p[i]>=a[i]){
  //如果i是峰，不管如何降低a[l[i]]或a[r[i]]都无法增加排水格数
    to=max(a[l[l[i]]],query(l[i]+1,i-1));
    v[l[i]]+=(p[i]-max(to,a[i])>0?
      p[i]-max(to,a[i]):0);//讨论左峰

    to=max(a[r[r[i]]],query(i+1,r[i]-1));
    v[r[i]]+=(p[i]-max(to,a[i])>0?
      p[i]-max(to,a[i]):0);//讨论右峰
  }
}

因此，\(ans\) 就可以这样求：

for(register int i=1;i<=n;i++)
  ans=min(ans,s-v[i]);

两类情况讨论完毕，上总 Code！

#define by_wanguan
#include<iostream>
#include<cstring>
#define ll long long
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
using namespace std;
const int N=1e6+7;
ll l[N],r[N],a[N],T,n,v[N],p[N],w[N],s,ans,to;
ll read(){ll x=0,w=1;char ch=0;while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}while('0'<=ch&&ch<='9'){x=(x<<3)+(x<<1)+(ch-'0');ch=getchar();}return x*w;}
void write(ll x){int sta[24],top=0;if(x<0){putchar('-');x=-x;}do{sta[top++]=x%10;x/=10;}while(x);while(top)putchar(sta[--top]+'0');}

/*
l[i] i左边最高位置   r[i] i右边最高位置 
a[i] i高度   p[i] i积水高度 
v[i] i两侧峰削去可减少积水格数
w[i] i积水格数 
*/

//ST表，不会去P3865
  ll lg2[N],pp[22],ma[N][21],len,lg,pl;
  inline void init(){
    pp[0]=1;
    for(register int i=1;i<=20;i++) pp[i]=pp[i-1]*2;
    int cnt=0,last=2;
    for(register int i=2;i<N;i++){
      if(i==last) cnt++,last*=2;
      lg2[i]=cnt;
    }
  }
  inline void solve(){
    for(register int i=1;i<=lg2[n]+1;i++)
      for(register int j=1;j<=n;j++)
        ma[j][i]=max(ma[j][i-1],ma[min(j+pp[i-1],n)][i-1]);
  }
  inline int query(int l,int r){
    if(l>r) return 0;
    if(l==0) l=1;
    len=r-l+1,lg=lg2[len],pl=pp[lg];
    return max(ma[l][lg],ma[r-pl+1][lg]);
  }

signed main(){
  T=read();
  init();
  while(T--){
    n=read();
    for(register int i=1;i<=n;i++)
      a[i]=read(),ma[i][0]=a[i];
    solve();
    l[0]=0,l[1]=0;
    for(register int i=2;i<=n;i++)
      if(a[i-1]>=a[l[i-1]]) l[i]=i-1;
      else l[i]=l[i-1];
    r[n+1]=0,r[n]=0;
    for(register int i=n-1;i>=1;i--)
      if(a[i+1]>=a[r[i+1]]) r[i]=i+1;
      else r[i]=r[i+1];
    s=0;
    for(register int i=1;i<=n;i++){
      p[i]=min(a[l[i]],a[r[i]]);
      if(p[i]-a[i]>0) w[i]=p[i]-a[i];
      else w[i]=0;
      s+=w[i];
    }
    for(int i=1;i<=n;i++) v[i]=0;
    for(register int i=1;i<=n;i++){
      if(p[i]>=a[i]){
        to=max(a[l[l[i]]],query(l[i]+1,i-1));
        v[l[i]]+=(p[i]-max(to,a[i])>0?
          p[i]-max(to,a[i]):0);
        to=max(a[r[r[i]]],query(i+1,r[i]-1));
        v[r[i]]+=(p[i]-max(to,a[i])>0?
          p[i]-max(to,a[i]):0);
      }
    }
    ans=s;
    for(register int i=1;i<=n;i++)
      ans=min(ans,s-w[i]),
      ans=min(ans,s-v[i]);
    write(ans),putchar('\n');
  }
}

AC 记录。

后附

日志

v1.0 on 2023.07.31: 发布