暑假刷题记 A

标签：复杂度线段 times 暑假可以题记我们 dis

数据结构

Ice-cream Tycoon

平衡树 / 线段树二分。

对于平衡树而言，构造一个函数，求出拿到最便宜的所需数量的 ice-cream 的价格（利用类似于树上查排名的操作即可），比较该价格与所有钱数的差别即可。

对于线段树二分而言，利用数量的单调性，求出对应的节点，然后修改该节点前的所有被影响到的节点即可，或许用 zkw 线段树更为方便。

两者单次询问时间复杂度均为 $O(\log n)$，需要注意的是， FHQ 线段树的实现是注意分裂了就要合并。

New Year Tree

dfs 序 + 线段树。

利用 dfs 序维护与 LCA 和子树有关的问题比较常见（博客概述）。

由于颜色数小于 60，那么就用线段树维护区间异或和即可。时间复杂度为 $O(n \log n)$。

需要注意， builtin_popcount 针对的是 int 型整数，无法计算 long long 类型的数。

Ping-Pong

并查集 + 线段树。

首先，我们意识到两个区间能否到达是一条单向边，且两个区间间的关系只有三种情况。

对于两个可以互达的区间，显然，我们可以将他们合并为一个大区间，大区间的端点为 $\min(x_1, x_2), \max(y_1, y_2)$，我们可以用并查集来表示这种关系。

怎样判断两个区间是否有这样的关系？

考虑到每个区间的关系只与相对位置有关，我们先将所有点离散化。那么此时，最多的点的个数为 $2 \times 10^5$。我们完全可以利用一个 vector 存储每个点所在的区间。考虑到区间的长度一定单调递增，那么新增的区间一定不可能被其他区间所包含，那么此时，它与之前的区间要么可以互达，要么只能由其他区间到达它，要么毫无联系，此时，求与它能够互达的区间实际上是求它的两个端点处被多少区间经过。

再想到如果一个点一个点地打标记，时间复杂度过高。我们可以利用线段树，给一定的区间打标记，而不下传到每个子节点，使修改的时间复杂度达到 $O(\log n)$。

最终的询问即判断两个区间是否在同一个集合中或者两个集合是否互相包含。

Life as a Monster

平衡树 + 数学。

对于一个格点到另一个格点的距离，由于可以斜向走，故而我们所求的实际上是切比雪夫距离。

我们记切比雪夫距离为 $D<(x_1, y_1), (x_2, y_2)>$ = $min(|x_1 - x_2|, |y_1 - y_2|)$, 由于对于一个数 x 的绝对值 $|x| = \min(x, -x)$, 那么此时， $D<(x_1, y_1), (x_2, y_2)> = \min(x_1 - x_2, x_2 - x_1, y_1 - y_2, y_2 - y_1)$

我们知道两个点间的曼哈顿距离 $d<(x_1, y_1), (x_2, y_2)>$ = $|x_1 - x_2| + |y_1 - y_2|$
= $\max(x_1 - x_2, x_2 - x_1) + \max(y_1 - y_2, y_2 - y_1)$ = $\max(x_1 - x_2 + y_ 1 - y_2, x_1 - x_2 + y_2 - y_1, x_2 - x_1 + y_1 - y_2, x_2 - x_1 + y_2 - y_1)$(两者交叉相加)。

此时，倘若我们令任意点 $(x, y) =>(x + y, x - y)$, 我们发现：

$x_1 - x_2 + y_ 1 - y_2$ = $(x_1 + y_1) - (x_2 + y_2) + (x_1 - y_1) - (x_2 - y_2)$ = $2 \times (x_1 - x_2)$。

同理，我们可以得到：

$d<(x_1, y_1), (x_2, y_2)>$ = $\max(2x_1 - 2x_2, 2y_1 - 2y_2, 2y_2 - 2y_1, 2x_2 - 2x_1)$。

于是，我们有一个结论，任意两格点间的切比雪夫距离是这两个格点通过 $(x, y) => (x + y, x - y)$ 转化后的曼哈顿距离的一半。

因此，我们可以将所有点转化为 $(x, y) => (x + y, x - y)$ 意义下的点，然后求任意一点到 n 个点的曼哈顿距离。考虑到曼哈顿距离中的 x 和 y 没有关联，而唯一限制是绝对值，我们可以利用两颗平衡树分别维护 x 和 y 的值，每次计算时查询小于给定值的数的个数即可，然后分别计算答案即可。

Tourists

圆方树 + 树链剖分。

因为要求不能重复经过一个点，故而一个点双联通分量中的点可以互达。于是想到把图中的点双缩点，维护圆方树，把方点的值设为它周围的圆点中点权最小的点的点权。通过树链剖分的方式求解路径上的最小值。

对于修改操作，每次维护方点即可，考虑对每个方点建立 multiset 储存每个方点周围的原点的权值，每次操作修改对应的方点即可。

此外，每次修改时可以仅修改圆点的父节点(方点), 而不是修改与圆点相连的所有方点。我们考虑每次修改一个圆点，如果圆点位于叶子节点上，此时只有一个方点与它相连，故而修改父亲节点即可；如果圆点不在叶子节点上，此时可以发现，如果一个路径会用到该圆点的信息，那么该路径一定会经过该圆点。故而这样的做法不会影响正确性。

New Year and Conference

线段树优化。

考虑到我们选择活动时，最少只需要选择两个，倘如我们选择更多的活动，如果此时冲突，那我们一定能分离出两个相冲突的活动。

这样，我们实际上是求是否存在两个活动，使其在一个会场冲突，另一个不冲突，暴力时间复杂度 $O(n^2)$ 。

我们考虑优化。我们先将活动分别按照第一会场和第二会场经行时间排序，那么此时，一个活动可以被举行当且仅当它与之前的活动在两个会场之一没有冲突。

此时，问题就被转化为：

查询满足 $r_j \ge r_i$ 中，$x_j$ 的最大值。如果最大值比 $y_i$ 大，那么就直接不合法。
查询满足 $r_j \ge r_i$ 中，$y_j$ 的最小值。如果最小值比 $x_i$ 小，那么直接不合法。

故此，我们可以用线段树优化这个过程，以一个会场的活动举办时间为轴，维护另一个会场的活动举办时间，总时间复杂度为 $O(n \log n)$ 。

Tree Generator™

dfs序 + 线段树。类似的

这个题应该很容易联想到 dfs序维护直径的方法，但题意的转化较难。

关键在于将左括号赋值为 $1$，右括号赋值为 $-1$。我们若将左括号看成向下走一步，右括号看成向上走一步，那么，对于任意一个点而言，该节点的深度是该节点到括号序列最左端之间，右括号的数目减去左括号的数目，
也就是该节点左侧的 {1， -1} 序列的加和。

当我们知道每个节点的相对深度之后，由于树上任意两点 $u, v$ 间的距离为 $dep_u + dep_v - 2 * dep_{lca}$，因此我们可以仿照 dfs序 + 线段树的方式，维护树上任意两点间的最大距离，即我们所要求的直径。

Roadside Trees

线段树 + Dp

对于每棵树的高度，令 T 为此时时刻， t 为种植时间，那么此时树的高度为 $h + T - t$ 。由于我们只关心树的相对高度，因此我们可以假设每棵树的高度为 $h - t$ 恒定不变。

考虑种树操作，每次在一个位置种一棵树。由于每次种树的高度不超过 10，且每个树的高度不同，故最多只有 10 棵树比现在这棵树矮。
考虑砍树操作，在一个位置种一棵树，下标小于 10。

gg..

数学

Strange Limit

给定 $p$ 和 $m$, 令 $a_1 = p, a_{n + 1} = p^{a_n}$, 求 $\lim\limits_{n \rightarrow + \infty}(a_n \mod m!)$ 。

我们知道， $a = p^{p^{p^{.^{.^{.}}}}}$。考虑欧拉定理 : 如果 $a$ 和 $n$ 互质，则有 $a^{\phi(n)} \equiv 1 (\bmod n)$。那么对于任意的 $a, b, n, $ 有 $a^b \equiv a^{\phi(n) + b \mod \phi(n)} (\bmod n)$(拓展欧拉定理)。

对于本题，由于 b 趋近于无穷，那么 $b \mod \phi(n)$ 趋近于 $\phi(n)$，我们可以不断递归，由于 $\phi(n)$ 的值不断减小，当 $\phi(n)$
递归到 1 时，就可以返回。

GCD Determinant

结论题，详见。

图论

B:Fairy

我们知道，一个图是二分图当这个图中不存在奇环。

这意味着我们要删除的边要将图中的所有奇环破坏掉(如果存在)。当存在多个奇环时，我们选择的边所有奇环的并集。

gg..

D:Connecting Cities

首先有一个不得不做的转化，将 $|i - j| \times D + a_i + a_j$ 看成 $\min((a_i + i \times D) + (a_j - j \times D) , (a_i - i \times D) + (a_j + j \times D))$。

这样的话我们可以通过维护 $a_i + i \times D$ 和 $a_i - i \times D$ 来得到我们要求的式子的结果，反正比带个绝对值的式子好维护。

然后由于我们实际上要求一棵最小生成树，那么可以从 kruskal 和 Prim 两种常见的最小生成树算法考虑。

对于 kruskal 而言，如果直接暴力建图的话会有 $n ^ 2$ 条边。考虑到有一些边是一定不会被 kruskal 算法选择的，那么可以考虑优化建图。这里我的建图方式来自于 lemondinosaur。我们可以考虑分治，由于我们每次将序列分成两块，两块间有明显的左右关系，我们令左块中元素的编号为 i ，右块中元素的编号为 j ，那么两者间边的权值为 $a_i - i \times D + a_j + j \times D$。

我们可以在左块中找到最小的 $a_i - i \times D$ , 将该点与右块中的所有的点连边；在右块中找到最小的 $a_i + i \times D$，将该点与左块中的所有点连边，相当于在两个块中找到最优点来代替两个块所有元素互相连边。由于我们要找的是最小的边使得两个块联通，所以这种方式一定是最优解。最后跑一边 kruskal 即可。总建边数为 $n \times \log n$，总时间复杂度为 $O(n \log^2n)$

对于 Prim 而言，我们考虑它的暴力流程，发现实际上我们需要维护的是最小的边权 和最小边权是由 哪个未被连接的点 和已连接的点组成的。

线段树维护的思路来自于 200815147
。我们还是将所求式子的绝对值拆开，通过线段树来维护边权的最小值，再记录一个标记，表示组成最小边的点的标号。那么现在的问题是 Prim 要求
我们选择的两个点，一个位于已经被选择的点集中，另一个位于还没有被选择的点集中。

我们考虑利用两类数组来区分这两种点，当一个点被选中时，将其对应的一类数组清空，另一类数组赋值。每次计算两个点间的距离时，只用这两种数组交错而形成的边，这样线段树维护的边权始终是未被选择的点和已被选择的点间的距离。总时间复杂度为 $O(n \log n)$

似乎这道题还有模拟 Boruvka 算法的，这里，用树状数组解题。

总的来说，这道题还是比较好的，每一种最小生成树的算法都可以解题，而每种解题方式都有共同点，也有各自的特色。

E:Tournament

如果一位选手在任意一个项目上可以打败对手，我们即从这位选手向他的对手连一条边。这样会形成很多个有向环，于是考虑缩点，在所形成的 DAG 上，入度为 0 的缩点中包含的点的数目即为所求。

F:Case of Computer Network

对于一个 E-BCC，我们总可以给其内部的边安排一个定向方式，使得其任何一个点都可以到达另外所有点。即 E-BCC 一定可以定向为 SCC。

我们可以考虑边双缩点得到一棵树，那么 s 到 t 的路径是唯一且固定的，即这些边的定向已经确定。倘若存在一条边的定向矛盾，即可判断无解。

可以通过 LCA + 差分的方式, 将对边的标记转化为对点的标记，用两个差分数组分别记录从该点向上走还是向下走，当一个点同时被标记时判断无解。时间复杂度 $O(m + (n + q) \log(n))$。

不经过 $s - t$ 最短路， $ans = dis(u, v)$。
$u$ 从 $x$ 接入 $stDAG$, 从 $y$ 离开 $stDAG$ 前往 $v$， $ans = dis(u, x) + dis(y, v)$。
$v$ 从 $x$ 接入 $stDAG$, 从 $y$ 离开 $stDAG$ 前往 $u$， $ans = dis(v, x) + dis(y, u)$。

我们可以先对 $u, v$ 跑单源最短路，预处理 $dis(u, ?)$ 和 $dis(v, ?)$。

如何找到最小的 $x, y$ 使 $ans$ 最小？考虑在 $stDAG$ 上的 $DP$。

我们令 $dpu_i$ 表示 $s - i$ 路径上最小的 $dis(u, i)$， $dpv_i$ 表示 $s - i$ 路径上最小的 $dis(v, i)$。

那么当我们将 $i$ 视为 $y$ 时， $ans = \min(dpu(i) + dis(u, i), dpu(i) + dis(v, i))$。

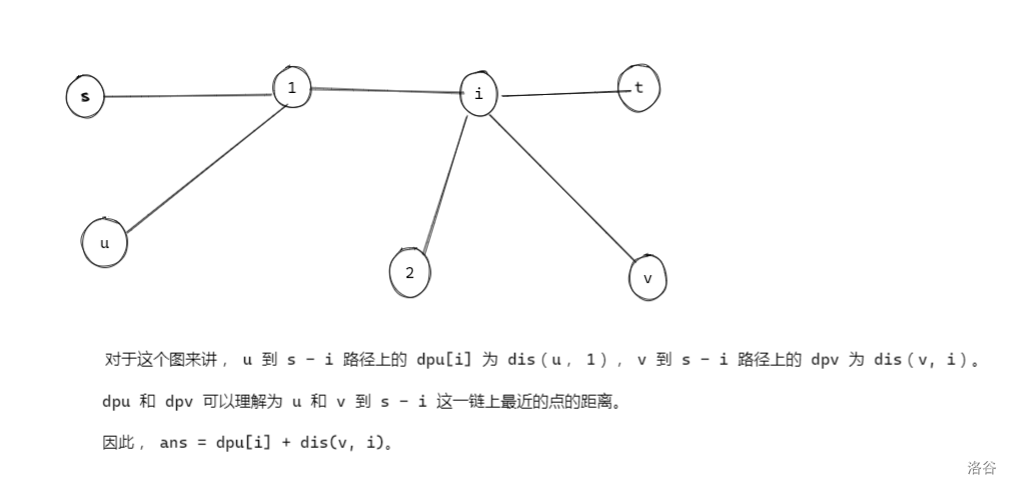
故而，在求出 dpu 和 dpv 之后，我们可以直接枚举 i 得到答案。

对于正边权图，只要维护 vis 使得每个点只会被拿出来一次，Dijkstra 拿出来的顺序就是在单源最短路 DAG 上的拓朴排序。

我们可以从 s 做一遍 dijkstra，得出 dpu 和 dpv。

P:Delivery Oligopoly

标签：复杂度,线段,times,暑假,可以,题记,我们,dis
From： https://www.cnblogs.com/ademik/p/17593793.html