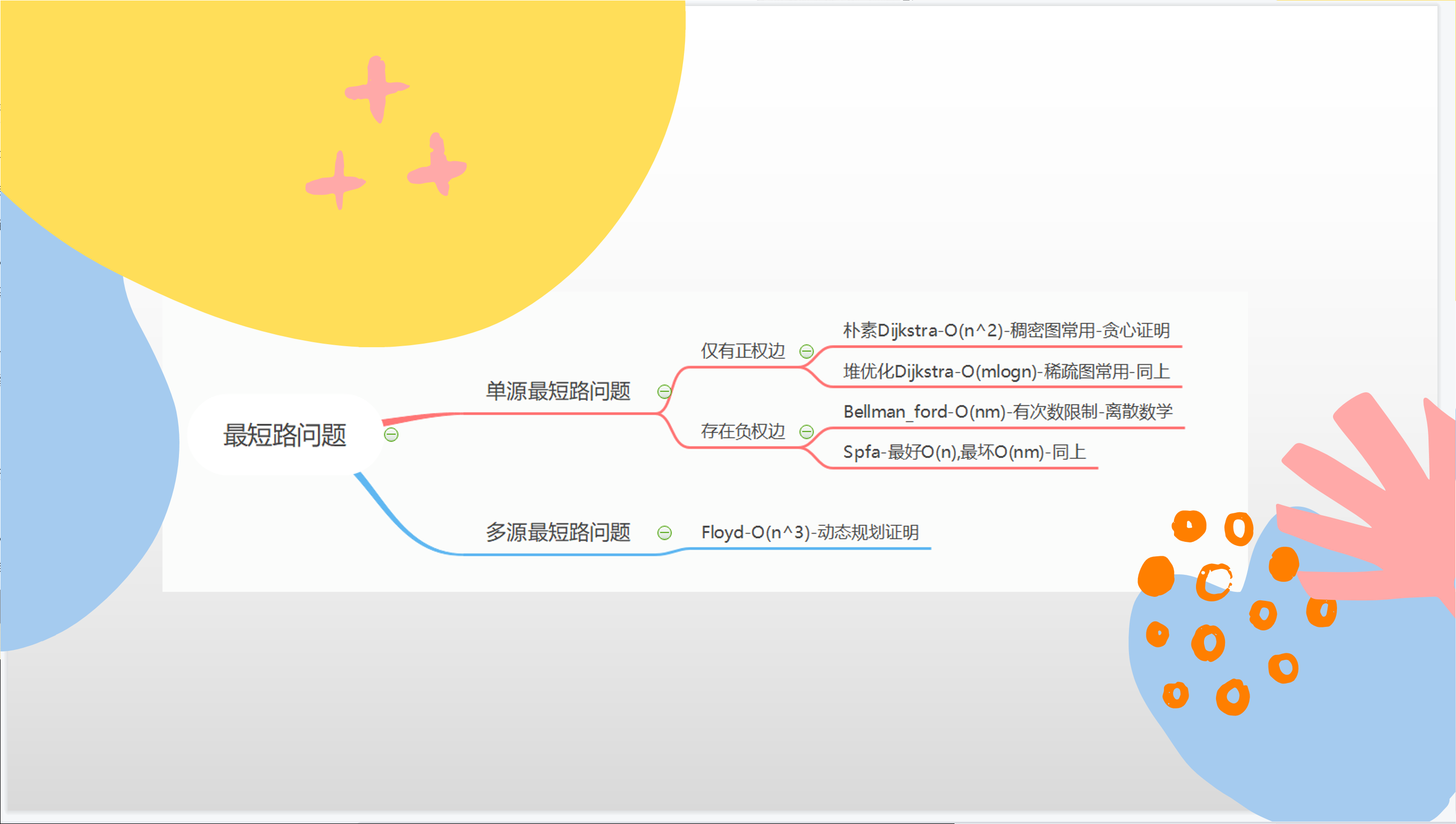
最短路
- 单源最短路
- 所有边权都是正数
- 朴素版Dijkstra算法(适用于稠密图)
- 堆优化版Dijkstra算法(适用于稀疏图)
- 存在负权边
- Bellman_Ford算法,用于仅存在负权边,并且对边数有限制
- Spfa算法 对Bellman_Ford算法进行优化(容易被卡死)
- 多源汇最短路 可能不止一个起点,有很多询问,求任意两个点之间的最短路径。
- Floyd算法

朴素版Dijkstra算法
稠密图:用邻接矩阵来存,稀疏图:用邻接表来存
模板
int g[N][N]; // 邻接矩阵存储图
bool st[N]; // 表示某个节点是否已经确定了最短路径
int dist[N]; // 存储1号点到x点的最短距离
int dijsktra(){
memset(dist, 0x3f, sizeof dist); // 初始化dist数组
dist[1] = 0; // 起点
for(int i = 0; i < n - 1; i ++){ // 起点的最短距离已经确定,迭代次数n-1次
int t = -1; // 用t来找当前所有未确定距离的点里最近的点
for(int j = 1; j <= n; j ++){
if(!st[j] && (t == -1 || dist[j] < dist[t]))
t = j;
}
for(int j = 1; j <= n; j ++){ // 用最近的点t来更新其它点距离
dist[j] = min(dist[j], dist[t] + g[t][j]);
}
st[j] = true;
}
if(dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
例题
849 Dijkstra求最短路
堆优化版Dijkstra算法
模板
朴素的Dijkstra算法适用于稠密图
typedef pair<int, int> PII;
// 复用了堆的pair自动排序的功能
priority_queue<PII, vector<PII>, greater<PII>> q; // pair.first = dist, pair.second = point_id
const int N = 1.5e5 + 10;
int h[N], e[N], ne[N], idx, W[N]; // 邻接表存稀疏图
int dist[N]; // 存储1 ~ i的最短距离
bool st[N]; // 判断节点是否已经确定了最短距离
int n, m;
int dijsktra(){
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
q.push({0, 1});
while(q.size()){
auto t = q.top();
q.pop();
int d = t.first, u = t.second;
// 注意,无论是否是堆优化版的算法,st[]的更新都是在确认是最短点之后。
if(st[u]) continue;
st[u] = true;
for(int i = h[u]; i != -1; i = ne[i]){
int j = e[i], distance = W[i]; // distance表示i - j 的距离
if(!st[j] && dist[j] > distance + d){
dist[j] = distance + d;
q.push({dist[j], j});
}
}
}
if(dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
例题
850. Dijkstra求最短路
Bellman_Ford算法
求包含负权边的单源最短路径算法。原理是:连续进行松弛操作,在每次松弛操作中,将每一条边都更新一次。如果最后一次松弛后,最短距离仍然能够更新,说明图中存在负环。无法到达最后节点。
因为假设1~n是可达的,通过循环n次操作(实际上n-1次就可以),就一定能到达n点。如果1-n中存在负环,那么循环n次,dist[n]最短距离还会继续减小。所以无法到达。
主要处理负权边
储存方式
struct Edge
{
int a,b,w;
}edge[M];
模板
// 存边
struct Edge{
int a,b,w;
}edge[M];
int bellman_ford(){
memset(dist, 0x3f, sizeof (dist));
// 注意初始初始节点还是要置0
dist[1] = 0;
// 注意这里的循环次数是有实际物理含义的:k次表示最多只经过k条边
// 如果题目没有限制经过边的数量,k替换为n(节点总数),不能是n-1, 可能存在负环。
for(int i = 0; i < k; i++){
memcpy(backup, dist, sizeof(dist)); // 备份的含义是,让此次迭代更新距离的所有结果都是来自上一次迭代。
for(int j = 0; j < m; j ++){
int a = edges[j].a, b = edges[j].b, w = edges[j].c;
dist[b] = min( dist[b], backup[a] + w ); // 边权的更新方式--- 松弛操作
}
}
// 这里使用> 0x3f3f3f3f /2 表示距离到不了,是因为可能存在负权回路,当无解时,可能dist[n] = 0x3f3f3f3f
// 加上一个负权
if(dist[n] > 0x3f3f3f3f / 2) return 0x3f;
return dist[n];
}
循环完所有边之后,就有一个等式成立:dist[b] <= dist[a] + w
注意:如果有负权回路(负环),可能最短路是不存在
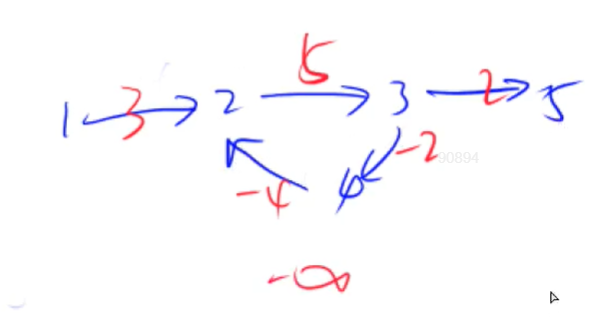
当进去2->3->4距离不断减小直到负无穷
最外层循环次数k, 表示经过不超过k条边的最短路的距离。所以,当题目有负环,并且对于经过的边的数量有限制时,选择bellman_ford算法。
例题
853. 有边数限制的最短路
Spfa算法
SPFA是对Bellman_ford算法的一个改进,时间复杂度最坏是O(nm), 通常是O(m); 所以即使是正权边,能用Dijkstra算法求解的问题,也一般能用SPFA来求解。
思路
for 1 ~ n: //注意这里的循环次数是有实际物理含义的
备份dist中的所有数据到backup数组中; // 备份的含义是,让此次迭代更新距离的所有结果都是来自上一次迭代。
for 所有边 a,b,w: // 表示一条从a 走向 b 的边,边权是w
dist[b] = min(dist[b], dist[a] + w); // 边权的更新方式--- 松弛操作
以上的松弛操作里,实际上dist[b]更新的时候,一定是dist[a]变小了,dist[b]的更新才会减小;用宽度优先搜索来做优化, 设置一个队列,存储距离变小了的结点,也叫待更新的点。
int n; // 总点数
int h[N], w[N], e[N], ne[N], idx; // 邻接表存储所有边
int dist[N]; // 存储每个点到1号点的最短距离
bool st[N]; // 存储每个点是否在队列中
// 求1号点到n号点的最短路距离,如果从1号点无法走到n号点则返回-1
int spfa()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
queue<int> q;
q.push(1);
st[1] = true;
while (q.size())
{
auto t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
if (!st[j]) // 如果队列中已存在j,则不需要将j重复插入
{
q.push(j);
st[j] = true;
}
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
例题
851. spfa求最短路
852. spfa判断负环
Floyd算法
主要用于处理:多源汇最短路算法
初始化:
存储图:邻接矩阵;d[i][j];
// 注意for循环的顺序,以最外层的k作为中间节点
void floyd(){
for( k = 1; k <= n; k++){
for( i = 1; i <= n; i++){
for( j = 1; j <= n; j++){
d[i][j] = min(d[i][j] , d[i][k] + d[k][j])
}
}
}
}
d[i,j]存储的就是从i到j的最小路。