首页 > 其他分享 >树状数组

树状数组

时间：2023-07-25 17:24:35浏览次数：38  
标签：idx 树状 int 查询 数组 区间 op

树状数组

定义

  • 设树状数组为 C ，x的末尾有 k 个0，则C[x] 表示 A 数组中 A [X - 2^k + 1, x] 的和

  • 使用lowbit(x) = x & (-x) 可以得到 2 ^ k 的值

应用

  • 维护单点修改前缀和的数据结构

  • 一个树形结构模型，支持单点修改，查询一个点 x 的前缀和

  • 通俗来讲

  • 可以动态维护一个序列

  • 支持单点修改，查询前缀和

  • 在信息可减的情况下

  • 可以各种差分：

    • 单点加，区间查询

    • 区间加，单点查询

    • 区间加，区间查询

特点

  • 树形结构的每个节点表示序列上的一个子集

  • 为了修改高效，每个序列上的位置只出现在少数个树形结构的节点上

  • 为了查询高效，对任意查询，可以通过少数个树形结构的节点拼出来

科普常识

  • 树状数组有几个叫法？

    • 二叉索引树 （Binary Index Tree)

    • Fenwick Tree

经典的图

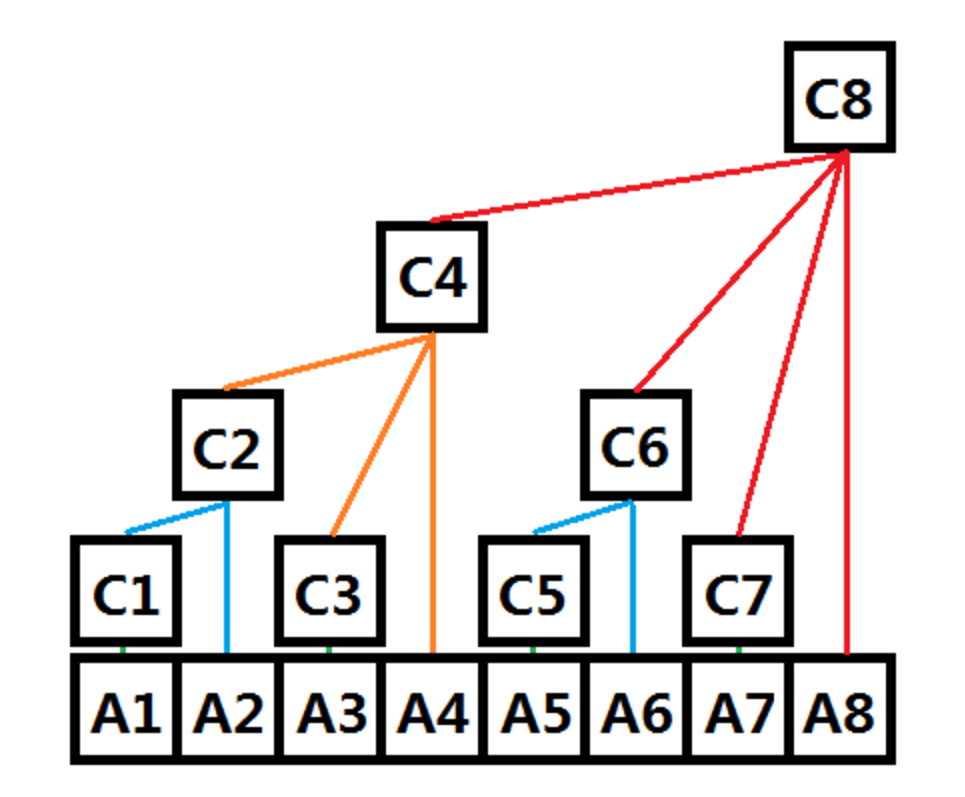
树状数组详细讲解，不会算法也能看懂哦 知乎

原理

  • 树状数组是个什么玩意？假设序列为 A[1] ~ A[8]

  • 树状数组有以下特点

    • 一颗满二叉树，满二叉树的每个结点对应 A[]中的一个元素。

    • 设树状数组为 C[]

观察一下，每个 C 代表了哪些 A

  • C[1] = A[1]

  • C[2] = A[1] + A[2]

  • C[3] = A[3]

  • C[4] = A[1] + A[2] + A[3] + A[4]

  • C[5] = A[5]

  • C[6] = A[5] + A[6]

  • C[7] = A[7]

  • C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]

具体原理没搞懂也没事，直接背下来怎么写都行，因为代码很短

可以简单的抽象为一个数据结构的功能

  1. 修改一个位置的值

  2. 查询一个前缀的某个可以合并的信息

  3. 也可以看成删去了右儿子的线段树

性质

  • 我们查询一个前缀的和， 可以用 O(log n) 个树状数组的节点拼起来，刚好拼得这个前缀和

  • 这O(log n)的节点怎么求呢？

    int Sum(int i){ // 返回前 i 个元素和
    int s = 0;
    while(i > 0){
        s += C[i];
        i -= i & (-1);
    }
    return s;

}

查询

  • 查询 x 的前缀和

  • 先看 C[x]

  • 设设树状数组为 C ，x的末尾有 k 个0，则C[x] 表示 A 数组中 A [X - 2^k + 1, x] 的和，迭代下去计算 x - 2 ^ k + 1 = x - 2 ^ k的前缀和，迭代到 0 的时候停止

  • 而 x - 2 ^ k 也就是 x - lowbit(x) ， 于是我们可以这样写

    int find(int x)
{
    int ans = 0;
    for(int i = x; i ; i -= lowbit(i))
        ans += t[i];
    return ans;
}

修改

  • 对于修改 y， 任何 C[x] 满足 x >= y,如果C[x] = A[x - 2 ^ k + 1, x],且 y 在 [x - 2 ^ k + 1, x] 中，则需要修改 C[x] 的值

  • 如何找出 C[x]？

  • 假设我们修改了 C[x] ，则 y 在 [x - 2 ^ k + 1, x] 中，于是 y 一定在 [(x + 2 ^ k) - 2 ^ {k + 1} + 1, (x + 2 ^ k)] 中，这里x的lowbit 是 2 ^ k 也需要更新

  • 修改可能显得不那么直观，可以根据线段树理解一下，实际上我们每次加的就是线段树上这个父亲节点的右儿子的大小。

    void modify(int x, int y)
{
    for(int i = x; i <= n; i += lowbit(i))
        t[i] += y;
}

单点加，区间查询

操作：

查询区间为 [l, r] 的时候，差分为前 r 个数的和减去前 l - 1 个数的和

区间加，单点查询

换个思路：

把区间 [l, r] 加差分为前缀 r 加， 前缀 l - 1 减

查询单点的时候只需要查询包含这个点的所有前缀修改

构建

最简单的方法是把每个数插进去

是 O(nlog n)

代码

  • 把 a[x] 加上 y

    #define lowbit i & -i
void modify (int x, int y)
{
    for(register int i = x; i <= n; i += lowbit(i))
        t[i] += y;
}

  • 求前 i 个数的和

    int find(int x)
{
    int ans = 0;
    for(register int i = x; i ; i -= lowbit(i))
        ans += t[i];
}

例题

逆序对

P1908 逆序对

题目大意：

  • 给定一个序列，求逆序对的个数

  • 逆序对即(i, j) 满足 i < j 且 a[i] > a[j] 的对

Solution

  • 进行离散化，然后按值域开树状数组

  • 然后扫这个序列

  • 现在扫到 i ，即查询前缀有多少大于 a[i] 的数

  • 然后把 a[i] 插入树状数组即可

代码：
#include <bits/stdc++.h>

#define MAXN 500001
#define lowbit(x) x & (-x)

using namespace std;

int n;
int a[MAXN], c[MAXN], hash[MAXN];
inline int read(){
    int x = 0;bool f = 0;char c = getchar();
    while(c < '0' || c > '9'){if (c == '-')f = !f;c = getchar();}
    while(c >= '0' && c <= '9'){ x = x * 10 + c - '0';c = getchar();}
    return f ? -x : x;
}

void add(int x){
    while(x <= n){
        c[x]++;
        x += lowbit(x);
    }
}

int sum(int x){
    int ans = 0;
    while(x){
        ans += c[x];
        x -= lowbit(x);
    }
    return ans;
}

int main(){
    long long ans = 0;
    n = read();
    for(int i = 1;i <= n; ++ i){
        a[i] = read(),hash[i] = a[i];
    }
    sort(hash + 1,hash + n + 1);
    for(int i = 1;i <= n; ++ i){
        int x = lower_bound(hash + 1,hash + n + 1, a[i]) - hash;
        add(x);
        ans += i - sum(x);
    }
    cout << ans << '\n';
    return 0;
}

不等式组

P5482 [JLOI2011] 不等式组

题目大意：

我们需要维护一堆不等式

  1. 插入一个 ax + b > c 的不等式

  2. 删除第 i 个插入的不等式

  3. 查询 x = k 时，成立的不等式个数

Solution

  • ax + b > c

    x > (c - b) / a

  • 开个值域上的树状数组

  • 然后每次插入取个整

  • 查询直接查前缀和

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5+10;
const int M = 2e6+10;
const int B = 1e6+1;//偏移量 
const int mx = 1e6+B;
//记下第i条不等式进行了什么操作 
int idx;
struct Node{
    int l,r;
    bool st;
}op[N];
//BIT Begin
int tree[M];
int lowbit(int x){
    return x&(-x);
}
int query(int x){
    int res = 0;
    while(x){
        res += tree[x];
        x -= lowbit(x);
    }
    return res;
}
void modify(int x,int dx){
    while(x <= mx){
        tree[x] += dx;
        x += lowbit(x);
    }
}
void update(int l,int r,int dx){
    modify(l,dx);modify(r+1,-dx);
}
//BIT End
void add(int a,int b,int c){
    if(a == 0){
        if(b > c){
            op[++idx].st = 1;
            op[idx].l = 1,op[idx].r = mx;
            update(op[idx].l,op[idx].r,1);
        }else{
            op[++idx].st = 0;
        }
    }else if(a > 0){
        int l = (int)floor(((c-b)*1.0)/a) + 1 + B;
        if(l > mx) op[++idx].st = 0;
        else{
            op[++idx].st = 1;
            op[idx].l = max(1,l),op[idx].r = mx;
            update(op[idx].l,op[idx].r,1);
        }
    }else{
        int r = int(ceil(((c-b)*1.0)/a)) - 1 + B;
        if(r < 1) op[++idx].st = 0;
        else{
            op[++idx].st = 1;
            op[idx].l = 1,op[idx].r = min(r,mx);
            update(op[idx].l,op[idx].r,1);
        }
    }
}
void del(int num){
    if(op[num].st){
        update(op[num].l,op[num].r,-op[num].st);
        op[num].st = 0;
    }
}
int main(){
    int n;scanf("%d",&n);
    char s[10];
    while(n--){
        scanf("%s",s);
        if(s[0] == 'A'){
            int a,b,c;scanf("%d%d%d",&a,&b,&c);
            add(a,b,c);
        }else if(s[0] == 'D'){
            int num;scanf("%d",&num);
            del(num);
        }else{
            int x;scanf("%d",&x);
            printf("%d\n",query(x+B));
        }
    }
    return 0;
}

区间加查单点

  • 给定一个序列，支持区间加，或者询问一个位置的值

例题

小鱼比可爱（加强版）

P5463 小鱼比可爱（加强版）

其实这个题也能是个模版，but 问题是你就是开了高精度，也能挂……所以，还需要int_128，反正各种各样的毛病一大堆，不愧是 3k……

代码：
#include <bits/stdc++.h>

using namespace std;

#define maxn 1000010
#define _i __int128

int n;
int a[maxn];
_i tr[maxn],ans = 0;
struct disc{int x, y;};
bool compp(disc x,disc y){return x.x < y.x;}
void discretization(int *darr, int dn)
{
    static disc b[maxn];
    for(int i = 1;i <= dn;i ++)
    b[i].x = darr[i], b[i].y = i;
    sort(b + 1, b + dn + 1, compp);
    static int tot = 0; b[0].x = -9666;
    for(int i = 1;i <= dn;i ++)
    if(b[i].x != b[i-1].x)darr[b[i].y] = ++tot;
    else darr[b[i].y] = tot;
}
inline int lowbit(int x){return x & (-x);}
void add(int x, _i y)
{
    for(; x <= n; x += lowbit(x))
    tr[x] += y;
}
_i sum(int x)
{
    _i re = 0;
    for(;x >= 1;x -= lowbit(x))
    re += tr[x];
    return re;
}
int b[50],t = 0;
void write(_i x)
{
    if(x == 0)b[++t] = 0;
    while(x > 0)b[++t] = x % 10,x /= 10;
    while(t)printf("%d", b[t--]);
}

int main()
{
    scanf("%d", &n);
    for(int i = 1;i <= n;i ++)
    scanf("%d",&a[i]);
    discretization(a,n);//离散化
    for(int i = n;i >= 1;i --)
    {
        ans += sum(a[i] - 1) * (_i)i;//求解
        add(a[i], (_i)n - i + 1);//修改
    }
    write(ans);//输出
}
经典问题

  • 给一棵n个点的数，有点权

  • 对每个点 x ，求其祖先中有多少点点权比 x 小

  • n <= 10^6

HH的项链

P1972 [SDOI2009] HH的项链

题目大意：

序列，多次查询区间中有多少不同的数

Solution:

  • 对于每一个位置 i， 预处理出 pre[i] 表示 i 左边离 i 最近的 j 满足 a[i] == a[j]

  • 然后查询区间中的不同数，我们可以只把每个数在区间中最后一次出现时统计进去

  • 扫一遍数组，扫到每个右端点的时候，维护每个左端点对应的答案

  • 考虑怎么维护这个答案

  • 红色的箭头即每个数前面那个和其相等的数

  • 记这个 pre, pre[i] = j, 即表示 i 前面离 i 最近的 j，满足 a[i] = a[j]

  • 我们想对区间中每个出现的数，恰好统计一次

  • 如果一个数在区间中第一次出现，则上次的出现位置 pre[i] < l

  • 如果一个数在区间中不是第一次出现，则上次的出现位置 pre[i] >= l

  • 问题变为区间 [l, r] 中，满足 pre[i] < l 的 i 个数

  • 区间 [l, r] ，满足 pre[i] < l 的 i 的个数

  • 我们可以差分，将区间 [l,r] 差分为前缀 [1,r] ，减去前缀 [1, l - 1]

  • 问题变为前 x 个数中 pre[i] < l 的 i 个数

  • 考虑将询问离线，即先读入所有询问，后记录下来

  • 假设一个询问是对于区间 [l,r] 的，则我们在 r 的位置记录一下，我们这里有个询问，查询的是 < l 的元素个数，对答案贡献是正的

  • 在 l - 1 的位置记录一下，我们这里有个询问，查询的是 <l 的元素个数，对答案贡献是负的

  • 于是我们和逆序对问题类似，从 1 扫到 n，假设现在扫到了 i， 我们开一个值域上的树状数组存下前 i 个元素

  • 每次从 i 到 i + 1，即先将 i + 1 位置的值插入值域树状数组

  • 然后进行这个位置上的查询

  • 注意一个位置上可能有多个查询，但总共的查询次数是 O(m)

  • 总时间复杂度 O((n + m)log n)

代码
#include <iostream>
#include <algorithm>
#define lowbit(x) (x & -x)
using namespace std;

const int N = 1e6 + 10;
int n, m, a[N], res[N], f[N];
struct Query {
  int id, l, r;
} q[N];
int tr[N];

inline void add(int k, int x) {
  for (; k <= n; k += lowbit(k)) tr[k] += x;
}

inline int sum(int k) {
  int res = 0;
  for (; k; k -= lowbit(k)) res += tr[k];
  return res;
}

int main() {
  scanf("%d", &n);
  for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
  scanf("%d", &m);
  for (int i = 0; i < m; i++) {
    scanf("%d%d", &q[i].l, &q[i].r);
    q[i].id = i;
  }

  sort(q, q + m, [&](Query &q1, Query &q2) {
    return q1.r < q2.r;
  });

  for (int i = 1, k = 0; k < m; k++) {
    int r = q[k].r, l = q[k].l, id = q[k].id;
    for (; i <= n && i <= r; i++) {
      if (f[a[i]]) add(f[a[i]], -1);
      f[a[i]] = i;
      add(i, 1);
    }
    res[id] = sum(r) - sum(l - 1);
  }

  for (int i = 0; i < m; i++) printf("%d\n", res[i]);
}
Yazid 的新生舞会

P4062 [Code+#1] Yazid 的新生舞会

Solution

  • 令 x = 1 -> n

  • 求有多少区间出现次数过半的元素为 x

  • 和上题一样，我们把所有 x 出现的位置，其前后第一个非 x 的位置标记

  • 然后一个非 x 的位置没有被标记，等价于任何包含这个位置的区间，其内部 x 出现次数都 <= 其他值出现次数

  • 于是对答案有贡献的区间一定是被标记的连续区间的子区间

  • 这些连续区间长度和为 O(n)

  • 考虑每段被连续标记的区间

  • 将 x 位置设为 + 1， 非 x 位置设为 -1

  • 记 pre[i] = pre[i - 1] + (a[i] == x ? 1 : - 1)

  • 一个区间 (i, j) 对答案有贡献等价于 pre[j] - pre[i - 1] >0 且 j > i

  • 这个就是个顺序对，直接做就行

  • 总时间复杂度 O(nlogn)

代码
#include <bits/stdc++.h> 

using namespace std;

#define LL long long
#define pa pair<int,int>

const int Maxn = 500010;
const int inf = 2147483647;
int read()
{
    int x = 0, f = 1;char ch = getchar();
    while(ch < '0' || ch > '9'){ if(ch == '-')f = -1;ch = getchar();}
    while(ch >= '0' && ch <= '9')x = (x << 3) + (x << 1) + (ch ^ 48), ch = getchar();
    return x * f;
}
int n, a[Maxn], Next[Maxn], pos[Maxn], st[Maxn];
LL sa[Maxn << 1], sb[Maxn << 1], sc[Maxn << 1];
LL ans = 0;
void add(int x, LL op)
{
    LL a = (LL)1, b = (LL)3 - 2 * x, c = (LL)x * x - 3 * x + 2;
    x += n + 1;
    for(; x <= (n << 1) + 1; x += (x & -x)) sa[x] += a * op, sb[x] += b * op,sc[x]+=c*op;
}
void Add(int l,int r,LL op){add(l,op), add(r + 1, -op);}
void Query(int x,LL op)
{
    LL X = x;
    x += n + 1;
    LL a = 0,b = 0,c = 0;
    for(; x ; x -= (x & -x))a += sa[x], b += sb[x], c += sc[x];
    ans += op * (a * X * X + b * X + c);
}
int main()
{
    n = read(); read();
    for(int i = 1; i <= n;i ++)
    {
        a[i] = read();
        if( !pos[a[i]])st[a[i]] = i;
        else Next[pos[a[i]]] = i;
        pos[a[i]] = i;
    }
    for(int i = 0;i < n;i ++)
    if(st[i])
    {
        Add(-(st[i] - 1), 0, 1);
        int s = 0;
        for(int j = st[i]; j; j = Next[j])
        {
            s ++;
            int t;
            if(!Next[j])t = n;
            else t = Next[j] - 1;
            Query(2 * s - j - 1, 1);
            Query(2 * s - t - 2, -1);
            Add(2 * s - t, 2 * s - j, 1);
        }

        Add(-(st[i] - 1), 0, -1);
        s = 0;
        for(int j = st[i]; j; j = Next[j])
        {
            s ++;
            int t;
            if(!Next[j])t = n;
            else t = Next[j] - 1;
            Add(2 * s - t, 2 * s - j, -1);
        }
    }
    printf("%lld", ans >> 1);

标签：idx,树状,int,查询,数组,区间,op
From： https://www.cnblogs.com/Auditorymoon-yue/p/17580342.html

相关文章

  • element ui 的el-select的回显，v-model绑定的是一个数组，如何保证回显成功
    要确保`el-select`组件的回显成功，其中`v-model`绑定的是一个数组，你需要按照以下步骤进行操作：1.在`el-option`组件上使用`:value`属性设置每个选项的值，确保每个选项都有唯一的标识。2.在`el-select`组件上使用`:multiple="true"`属性来启用多选模式。3.在`mount......
  • 如何构造类似数组的数据结构？
    ..介绍在开始解决数组问题之前，理解并实现类似数组的数据结构是一个很好的实践。本课教您如何实现常见的数组操作，例如插入元素、删除元素、获取元素、求数组长度以及打印数组元素。我们正在建设什么？我们将从头开始构建一个数组，其中包含一些最常见的数组操作，如上所述。我们还将学习如......
  • 输出数组内每个元素的类型python
    输出数组内每个元素的类型PythonPython是一种简单而强大的编程语言，广泛用于数据处理和科学计算。在Python中，数组是一种重要的数据结构，它可以存储多个元素，并允许我们对这些元素进行操作。在本文中，我们将探讨如何输出数组内每个元素的类型，并提供相应的代码示例。什么是数组？在计算......
  • 数组的常见操作及其算法
    一、数组的常见操作1、定义一个int类型的数组，里面包含10个元素，分别赋一些随机数，然后求出这10个元素的最大值、最小值、总和、平均值。注：随机数公式：(数据类型)(最小值+Math.random()*(最大值-最小值+1))publicstaticvoidtest01(){//创建一维数组int[]a......
  • 翻转 实现数组元素倒序的方法
     在Java编程开发中，经常会遇到需要对数组进行操作的情况。其中一个常见的需求就是实现数组元素的倒序。本文将介绍一种简洁高效的方法来实现这个功能。在开始之前，我们需要先了解一下数组的基本概念。数组是一种容器，可以存储多个相同类型的数据。数组的元素可以通过索引来访问，索......
  • Java 字符串转整形数组的方法及注意事项
     在Java编程中，经常会遇到需要将字符串转换为整形数组的情况。这是一个常见的操作，它可以帮助我们更方便地处理数据。本文将介绍一些常见的方法和注意事项，以帮助您顺利完成字符串转整形数组的任务。方法一：使用split()方法split()方法是Java中常用的字符串分割方法，它可以按照指......
  • C++中定义一个二维数组
    在C++中定义二维数组有很多种方式1.第一种方式：定义一个二级指针(指向指针的指针)#include<iostream>usingnamespacestd;voidTraverse(int**p);intmain(){//two-dimensionarrayintm=3,n=5;int**arr=newint*[m];arr[0]=newint[n];arr[1......
  • LeetCode 热题 100 之 560. 和为 K 的子数组.md
    题目给你一个整数数组nums和一个整数 k，请你统计并返回该数组中和为 k 的连续子数组的个数 。示例1：输入：nums=[1,1,1],k=2输出：2示例2：输入：nums=[1,2,3],k=3输出：2提示：1<=nums.length<=2*10^4-1000<=nums[i]<=1000-10^7<=k<=10^7思路......
  • 树状数组学习笔记
     树状数组真的很精美，码量小，还很快，比线段树快多了[滑稽]。一维树状数组单点修改，区间查询例题：loj#130.树状数组1louguP9974【模板】树状数组1不多说，代码：#include<bits/stdc++.h>usingnamespacestd;constintN=5e5+5;intn,m,c[N];intlowbit(intk){......
  • 数组（Array）和链表（List）
    推荐https://cloud.tencent.com/developer/article/2304343引言在Java编程中，数组（Array）和链表（List）是常用的数据结构，用于在内存中存储和组织数据。两者都有各自的特点和适用场景，本文将深入比较数组与链表的区别，并结合代码示例进行详细解释。数组（Array）定义和特点数组是一种固定......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99