Codeforces Round #887 Div.2 一定要手玩哦
前言:
一定要手玩,一定要手玩!
我今早一手玩发现C很TM简单,如果赛时我能切C说不定直接上1800.。。。
时隔多年,我的Codeforces Rating(1718) 再次超越了 @cqbzlhy(1674)!!!

赛时错误:
- B题出得太慢了->劣于pzj半小时。%%%pzj
- C没有手玩,瞪眼半天看不出来
- D由于特判问题RE了两发!!!!!(还好不是WA不计罚时)
这次怎么DF全是构造啊。。。。。
要想题目考思维,数学构造加几何!
A-Desorting
简单题。找到差的最小值,将其除以2再加一就是答案。注意负数直接输出0.
B-Fibonaccharsis
题意:给定 \(n,k\) 求有多少个类斐波那契数列的第 \(k\) 项为 \(n\)。
有意思,设 \(Fib[1]=0,Fib[2]=1,Fib[n]=Fib[n-1]+Fib[n-2](n>2)\)。
注意到可以枚举该类斐波那契数列的第一项,则第二项显然是唯一的且具有单调性的。二分查找即可。
斐波那契数列增长非常快,\(Fib[n]=(\frac{\sqrt 5+1}{2})^n-(\frac{\sqrt 5-1}{2})^n\),指数级增长。故时间复杂度 \(O(n\log nk)\),实际上有效的 \(k\) 在 \(2\times 10^5\) 范围内是不超过35的。
if(n==0){
cout<<"1\n";continue;
}
if(k>35){
cout<<"0\n";continue;
}
int ans=0;
for(int i=0;i<=n;i++){
int l=i,r=n-i;
while(l<r){
int j=l+r>>1;
int a=i,b=j,tag=0;
for(int p=3;p<=k;p++){
int z=a+b;
if(p==k){
if(z>=n)r=j;
else l=j+1;
}
if(z>n){
r=j;break;
}
a=b,b=z;
}
}
int j=l;
int a=i,b=j,tag=0;
for(int p=3;p<=k;p++){
int z=a+b;
if(p==k&&z==n){
ans++;
}
if(z>n){
break;
}
a=b,b=z;
}
}
cout<<ans<<"\n";
事实上,这不够数学。
注意到类斐波那契数列 \(f\),\(f[1]=a,f[2]=b,f[3]=a+b,f[4]=a+2b,f[5]=2a+3b,f[6]=3a+5b……\),它的系数是斐波那契数列,所以事实上应该是枚举首项,根据系数关系直接推断的。(或者说丢番图方程范围内整数解个数?)
C-Ntarsis'Set
题意:
给定序列 \(a_1\sim a_n\),有集合 \(S=\lbrace 1,+\infty\rbrace\),定义一次操作为:将 \(S\) 中排名为 \(a_1\sim a_n\) 的数一次性删去。求 \(k\) 次操作后序列的最小值。
\(1\le n,k\le 2\times 10^5\)
由于我们只求最小值,所以先只关心最小值的变化情况。
例如在 \(a={1,3,5,6,7}\) 时,最小值分别为 \(1,4,9,14,19,24\)
观察多组数据,容易发现在 \(k\) 时刻的最小值和在 \(k-1\) 时刻的最小值之差 \(d_k\) 取决于 \(k\) 时刻最小值 \(x_k\) 大于等于的 \(a_i\) 的个数。
也即 \(d_k=\sum_{i=1}^n[x_k\ge a_i]\),这显然是单调不减的。我们可以维护 \(d\),用一个指针更新它,并不断累加最小值即可。
时间复杂度: \(O(n+k)\)
边界:\(x_0=0,d_0=0\)——>注意这样的话我们等价于求的是 \(S\) 从0开始的答案,所以最后要+1。
#include<iostream>
using namespace std;
int a[505050],n,t,k;
int main(){
ios::sync_with_stdio(false);
cin>>t;
while(t--){
cin>>n>>k;
for(int i=1;i<=n;i++)cin>>a[i];
int x=0,d=0;
while(k--){
while(d+1<=n&&a[d+1]<=x+d+1)++d;
x+=d;
}
cout<<x+1<<"\n";
}
}
学到的东西:
找规律问题可以关注 \(\Delta\) 的变化情况
手玩几组样例,明确关注点。
D-Imbalanced Arrays
要求构造一个长为 \(n\) 的数组b,满足以下条件:
- \(-n\le b[i]\le n\)
- \(\forall i,j\in[1,n],b[i]+b[j]\neq 0\)
- \(a[i]=\sum_{k=1}^n[b[k]+b[i]>0]\)
题解:注意到,若 \(b\) 的所有值的绝对值构成了一个 \(1\sim n\) 的排列,则必定满足条件 1,2
那么只需要考虑条件3。注意到 \(a[i]>a[j]\implies b[i]>b[j]\),而顺序在此题没有要求,只要我们记下每个 \(a\) 的id即可。将 \(a\) 从小到大排序,这就确定了大小关系。
这时候我们来考虑一个数为正数的条件:\(a[i]\ge n-i+1\),因为正数加上正数一定是正数。我们设 \(x\) 为满足 \(a[x]\ge n-x+1\) 的最小 \(x\) ,这个就是最小的正数。
那么 \(\forall i\ge x,a[i]\) 的意义是:绝对值小于它的负数的个数与其他正数的个数之和。于是 \(a[i]-(n-x+1)+j-x+1\) 就是 \(i\) 所代表的数字的绝对值的排名。由于它是正数,所以直接确定了它的值。
当我们确定完正数的值的时候,负数的值就把排列里剩下的数按大小关系分配即可(这个数可以算出来,用来判无解)。
最后判一下无解。
注意特判:当 \(a\) 全部为 \(0\) 时候,全输出 \(-1\) 即可。
struct node{
int id,x;
bool operator<(const node b){
return x<b.x;
}
}a[505050];
int b[505050],cnt[505050],tot,vis[505050];
int main(){
int t=read(),n;
while(t--){
for(int i=1;i<=n;i++)vis[i]=0;
n=read();tot=0;
for(int i=1;i<=n;i++)a[i].x=read(),a[i].id=i;
sort(a+1,a+n+1);
int x=-1;
for(int i=1;i<=n;i++){
if(a[i].x>=n-i+1){
x=i;
for(int j=i;j<=n;j++){
int p=a[j].x;p-=n-i+1;p+=j-i+1;vis[p]=1;
b[a[j].id]=p;
}
break;
}
}
if(x==-1){
cout<<"YES\n";for(int i=1;i<=n;i++)cout<<"-1 ";cout<<"\n";continue;
}
int j=1,k=0;
for(int i=x-1;i;i--){
while(vis[j]&&j<=n)++j,++k;
b[a[i].id]=-j;
if(n-x+1-k!=a[i].x){
b[a[i].id]=-n-1;
}
vis[j]=1;--k;
}
int tag=0;
for(int i=1;i<=n;i++){
if(b[i]>n||b[i]<-n){
cout<<"NO\n";tag=1;break;
}
}
if(tag)continue;
cout<<"YES\n";
for(int i=1;i<=n;i++)cout<<b[i]<<" ";cout<<"\n";
}
}
E-Ina of the Moutain
题意:给定数 \(a[1]\dots a[n]\),每一次可以任选一个区间,将区间中所有数减一,当某个数等于0后,将变为\(k\),问所有数变为 \(k\) 的最小操作次数。
首先,让我们思考一下如果没有这个模 \(k\)的限制,答案是多少。(思考简化版问题)
设 \(f[i]\) 为前 \(i\) 个数变 \(1\) 的最小操作次数,则 \(f[i]=f[i-1]+\max(0,a[i]-a[i-1])\)。当 \(a[i]>a[i-1]\) 时,先将 \(a[i]\) 调整为 \(a[i-1]\) 然后和 \(a[i-1]\) 合并操作即可。另一种情况:当 \(a[i-1]\) 被减到 \(a[i]\) 时合并操作即可。
那么我们考虑这个问题,逆向思考。
首先,假设我们已经知道了最优方案下每一个 \(a[i]\) 会被减到 \(b[i]\) 次 \(0\),等价于加了 \(b[i]\) 次 \(k\),则令 \(c[i]=a[i]+(b[i]-1)k\),问题就只剩下减小操作不会考虑变为 \(k\) 了。设 \(d[i]=c[i]-c[i-1]\),答案就为 \(\sum_{i=1}^n\max(0,d[i])\)。理论上,我们枚举每一种情况,计算该式的最小值就为答案。
让我们再来思考一些性质。直觉告诉我们必定存在最优方案使得每一个 \(d[i]<k\)。为什么?因为若 \(d[i]\ge k\),由于 \(c\) 非负,则 \(c[i]\ge d[i]\ge k\),将 \(c[i]\) 减去 \(k\),答案不可能变劣。重复这个操作,直到不存在 \(d[i]\ge k\) 为止(最多影响到 \(d[n]\),此时再减少 \(c[n]\)就可以了),我们仍能得到一个答案不变的最优方案。
那么我们来考虑计算答案。
不直观的序列问题,可以转化到平面上,尤其是做差求值,在平面上可以直接通过坐标差体现,转化为路径。
那么每个 \(c[i]\) 最多有两种可能。
我们将 \(c[i]\) 视作点 \((i,c[i])\),则在直线 \(x=i\) 上,最多只有两个合法的点,且距离等于 \(k\)。问题转化为求 \((0,0)\) 到 \((n+1,0)\) 的最短路。
这里的路径长度定义为:\(\sum_{i=1}^{n+1}\max(0,y_i-y_{i-1})\)
盗个图,例如 \(a={1,2,3,1,3,2,1}\) 的时候,有:
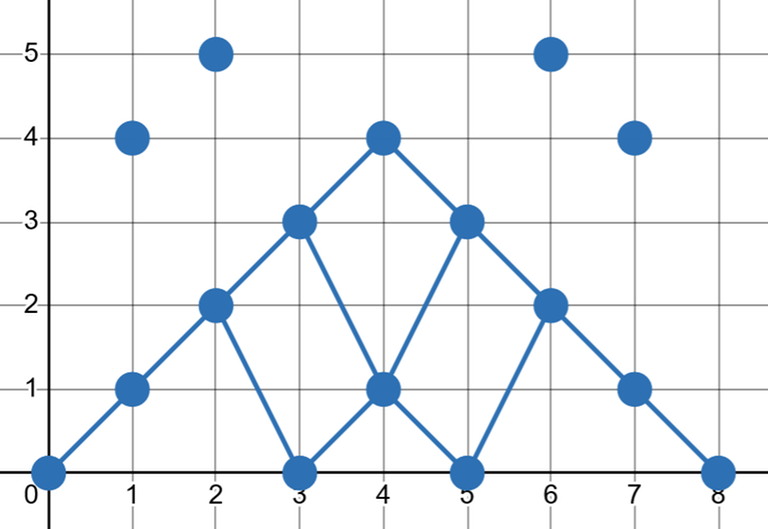
这里是这个题最魔幻的部分,也是最让人着迷的地方(w看了一个下午才懂。。。。)
那么这里显然有贪心策略:能往下走就往下走,走不下去了就往上爬。设走不下去的点为 \(i\)
但,这个往上爬是有技术含量的。可以在之前的某个位置 \(j\) 就向上爬了,代价为 \(k-y_j+y_{j-1}(y_j\le y_{j-1})\)。此时将 \(j\sim i\) 的点的 \(y\) 全部加上 \(k\) 就不会对答案有影响了。
那么我们就是要找到这个向上爬的最小代价。显然我们可以通过优先队列维护每一个向上爬的路。(对于每一个 \(a_i>a_{i-1}\),有向上的路径,长度为 \(a_i-a_{i-1}\),对于每一个 \(a_i<a_{i-1}\),有向上的路径 \(a_i+k-a_{i-1}\))。当然,\(a_i<a_{i-1}\) 相当于走下坡路,是最优选择。
代码是那么地简洁与优雅,令人着迷。
#define int long long
int n,t,k;
signed main(){
ios::sync_with_stdio(false);
cin>>t;
while(t--){
cin>>n>>k;
int lst=0,ans=0;priority_queue<int>q;
for(int i=1;i<=n;i++){
int x;cin>>x;x%=k;
if(x>lst){
q.push(-(x-lst));
ans-=q.top();
q.pop();
}
else q.push(-(k-lst+x));
lst=x;
}
cout<<ans<<"\n";
}
}
F-Miriany and Matchstick
看不懂,等我今晚爆肝
标签:le,887,lst,int,Codeforces,Fib,最小值,Div.2,正数 From: https://www.cnblogs.com/oierpyt/p/17578479.html