二分
二分查找
作用：
是用来在一个有序数组中查找某一元素的算法。
过程：
以在一个升序数组中查找一个数为例。
它每次考察数组当前部分的中间元素，如果中间元素刚好是要找的，就结束搜索过程；如果中间元素小于所查找的值，那么左侧的只会更小，不会有所查找的元素，只需到右侧查找；如果中间元素大于所查找的值同理，只需到左侧查找。
性质：
时间复杂度：
最优时间复杂度是 O(1)，
二分查找的平均时间复杂度和最坏时间复杂度均为 O(log n) 。因为在二分搜索过程中，算法每次都把查询的区间减半，所以对于一个长度为 n 的数组，至多会进行 O(log n) 次查找。
空间复杂度
迭代版本的二分查找的空间复杂度是 O(1) 。
递归版本的二分查找的空间复杂度是 O(log n)。
模版代码：
int binary_search(int start, int end, int key) {
int ret = -1; // 未搜索到数据返回-1下标
int mid;
while (start <= end) {
mid = start + ((end - start) >> 1); // 直接平均可能会溢出，所以用这个算法
if (arr[mid] < key)
start = mid + 1;
else if (arr[mid] > key)
end = mid - 1;
else { // 最后检测相等是因为多数搜索情况不是大于就是小于
ret = mid;
break;
}
}
return ret; // 单一出口
}
最大值最小化 和 最小值最大化
满足某种条件的最大值的最小可能情况（最大值最小化），首先想法是从小到大枚举作为答案的最大值，然后去判断是否合法。若答案单调，就可以使用二分搜索法来更快的找到答案。因此，想要使用二分搜索法来解决这种「最大值最小化」的题目需要满足以下 三个条件：
-
答案在一个固定区间内；
-
可能查找一个符合条件的值不是很容易，但是要求能比较容易的判断某个值是否符合条件的
-
可行解对于区间满足一定的单调性。换言之，如果 x 是符合条件的，那么有 x + 1 或者x - 1 也符合条件。（这样下来就满足了单调性）
当然，最小值最大化同理。
以下内容来自 oi-wiki
STL 的二分查找
C++ 标准库中实现了查找首个不小于给定值的元素的函数std::lower_bound和查找首个大于给定值的元素的函数std::upper_bound，二者均定义于头文件 <algorithm> 中。
二者均采用二分实现，所以调用前必须保证元素有序。
bsearch
bsearch 函数为 C 标准库实现的二分查找，定义在 <stdlib.h> 中。在 C++ 标准库里，该函数定义在 <cstdlib> 中。qsort 和 bsearch 是 C 语言中唯二的两个算法类函数。
bsearch 函数相比 qsort（排序相关 STL）的四个参数，在最左边增加了参数「待查元素的地址」。之所以按照地址的形式传入，是为了方便直接套用与 qsort 相同的比较函数，从而实现排序后的立即查找。因此这个参数不能直接传入具体值，而是要先将待查值用一个变量存储，再传入该变量地址。
于是 bsearch 函数总共有五个参数：待查元素的地址、数组名、元素个数、元素大小、比较规则。比较规则仍然通过指定比较函数实现，详见 排序相关 STL。
bsearch 函数的返回值是查找到的元素的地址，该地址为 void 类型。
注意：bsearch 与上文的 lower_bound 和 upper_bound 有两点不同：
- 当符合条件的元素有重复多个的时候，会返回执行二分查找时第一个符合条件的元素，从而这个元素可能位于重复多个元素的中间部分。
- 当查找不到相应的元素时，会返回 NULL。
用 lower_bound 可以实现与 bsearch 完全相同的功能，所以可以使用 bsearch 通过的题目，直接改写成 lower_bound 同样可以实现。但是鉴于上述不同之处的第二点，例如，在序列 1、2、4、5、6 中查找 3，bsearch 实现 lower_bound 的功能会变得困难。
利用 bsearch 实现 lower_bound 的功能比较困难，是否一定就不能实现？答案是否定的，存在比较 tricky 的技巧。借助编译器处理比较函数的特性：总是将第一个参数指向待查元素，将第二个参数指向待查数组中的元素，也可以用 bsearch 实现 lower_bound 和 upper_bound，如下文示例。只是，这要求待查数组必须是全局数组，从而可以直接传入首地址。
int A[100005]; // 示例全局数组
// 查找首个不小于待查元素的元素的地址
int lower(const void *p1, const void *p2) {
int *a = (int *)p1;
int *b = (int *)p2;
if ((b == A || compare(a, b - 1) > 0) && compare(a, b) > 0)
return 1;
else if (b != A && compare(a, b - 1) <= 0)
return -1; // 用到地址的减法，因此必须指定元素类型
else
return 0;
}
// 查找首个大于待查元素的元素的地址
int upper(const void *p1, const void *p2) {
int *a = (int *)p1;
int *b = (int *)p2;
if ((b == A || compare(a, b - 1) >= 0) && compare(a, b) >= 0)
return 1;
else if (b != A && compare(a, b - 1) < 0)
return -1; // 用到地址的减法，因此必须指定元素类型
else
return 0;
}
对于新手而言，建议老老实实地使用 C++ 中的 lower_bound 和 upper_bound 函数。
以上内容来自 OI-Wiki
竞赛图哈密顿问路径题
题目大意：
-
交互库有一张 n 个点的竞赛图
-
竞赛图指向的每对点都有恰好一条有向边的有向图
-
你每次可以问一条边的方向
-
你希望通过不超过 n[log n] 次操作找到该图的一条哈密顿链
分析：
明白一个定理：竞赛图的任意强连通子图必存在哈密顿回路
该定理成立，即可解决本问题
二分答案
干嘛用的？
解题的时候往往会考虑枚举答案然后检验枚举的值是否正确。若满足单调性，则满足使用二分法的条件。把这里的枚举换成二分，就变成了「二分答案」。
快快乐乐的例题时间：
题目大意：
伐木工人米尔科需要砍倒 M 米长的木材。这是一个对米尔科来说很容易的工作，因为他有一个漂亮的新伐木机，可以像野火一样砍倒森林。不过，米尔科只被允许砍倒单行树木。
米尔科的伐木机工作过程如下：米尔科设置一个高度参数 H（米），伐木机升起一个巨大的锯片到高度 
H ，并锯掉所有的树比 H 高的部分（当然，树木不高于 H 米的部分保持不变）。米尔科就得到树木被锯下的部分。
例如，如果一行树的高度分别为20，15，10，17，米尔科把锯片升到 15 米的高度，切割后树木剩下的高度将是 15，15，10，15!，而米尔科将从第 1 棵树得到 5 米木材，从第4 棵树得到 2 米木材，共 7 米木材。
米尔科非常关注生态保护，所以他不会砍掉过多的木材。这正是他尽可能高地设定伐木机锯片的原因。你的任务是帮助米尔科找到伐木机锯片的最大的整数高度 H!，使得他能得到木材至少为 M 米。即，如果再升高 1 米锯片，则他将得不到 M 米木材。
解题思路：
二分答案
参考代码：
int a[1000005];
int n, m;
bool check(int k) { // 检查可行性，k 为锯片高度
long long sum = 0;
for (int i = 1; i <= n; i++) // 检查每一棵树
if (a[i] > k) // 如果树高于锯片高度
sum += (long long)(a[i] - k); // 累加树木长度
return sum >= m; // 如果满足最少长度代表可行
}
int find() {
int l = 1, r = 1e9 + 1; // 因为是左闭右开的，所以 10^9 要加 1
while (l + 1 < r) { // 如果两点不相邻
int mid = (l + r) / 2; // 取中间值
if (check(mid)) // 如果可行
l = mid; // 升高锯片高度
else
r = mid; // 否则降低锯片高度
}
return l; // 返回左边值
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> a[i];
cout << find();
return 0;
}有疑问吗？
有？
-
为什么区间左闭右开？
因为搜到最后会是这个样子的：
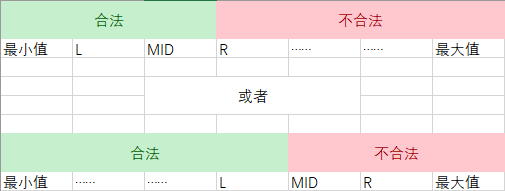然后会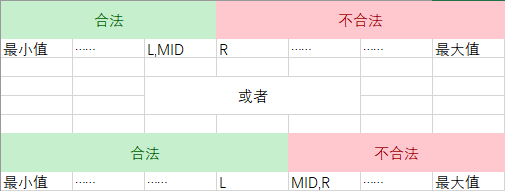
合法的最小值恰恰相反。