目录
浅谈字符串
\(\mathtt{-1}\) 前言
由于笔者字符串水平不高,可能会出现事实性的错误。
你说这篇博客会讲什么?我想大概会讲字符串技术巡礼中的前置知识(
\(\mathtt{0}\) 记号与约定
- 字符集记作 \(\Sigma\)。
- 一般使用 \(S,T\) 来表示一个字符串。
- 字符串 \(S\) 的长度(即包含的字符数量)记作 \(|S|\)。
- 空串为长度为 \(0\) 的唯一字符串,记作 \(\varepsilon\)。
- 字符串 \(S\) 的第 \(i\) 个字符记作 \(S_i\),字符串下标默认从 \(1\) 开始。
- 字符串 \(S\) 的一个子串 \(S[l,r]\) 为由 \(S_l,S_{l+1},\cdots,S_{r-1},S_r\) 组成的字符串。若 \(l>r\),\(S[l,r]=\varepsilon\)。
- \(S[1,i]\) 是字符串 \(S\) 的一个前缀,\(S[i,n]\) 是字符串 \(S\) 的一个后缀,其中 \(n=|S|\)。
- 对字符串 \(S\) 的一个子串/前缀/后缀 \(S'\),如果 \(S'\ne S\),则称 \(S'\) 是 \(S\) 的真子串/真前缀/真后缀。
- 若 \(S\) 是 \(T\) 的前缀,记作 \(S\sqsubseteq T\),特别的,如果 \(S\) 是 \(T\) 的真前缀,记作 \(S\sqsubset T\)。
- 对字符串 \(S,T\),\(S+T\) 定义为 \(S\) 和 \(T\) 的拼接。
- \(\operatorname{Rev}(S)\) 定义为 \(S\) 的翻转,有 \(\operatorname{Rev}(S)_i=S_{|S|-i+1}\)。
- 我们称字符串 \(S\) 为回文串,当且仅当 \(S=\operatorname{Rev}(S)\),即 \(S_i=S_{|S|-i+1}\)。
- \(\operatorname{LCP}(S,T)\) 定义为 \(\max\{i\mid i\le\min(|S|,|T|)\land S[1,i]=T[1,i]\}\)。
- \(\operatorname{LCS}(S,T)\) 定义为 \(\max\{i\mid i\le\min(|S|,|T|)\land S[|S|-i+1,|S|]=T[|T|-i+1,|T|]\}\)。
- 对于两个字符串 \(S,T\),我们称 \(S\) 字典序小于 \(T\),记作 \(S<T\),当且仅当 \(S\sqsubset T\) 或存在 \(i\) 满足 \(S[1,i-1]=T[1,i-1]\) 且 \(S_i<T_i\)。
其实就是抄的 ix35 的博客
\(\mathtt{1}\) 字符串 Hash
Hash 的思想是将不方便存储/比较的东西(比如字符串)通过 Hash 函数 \(f(s)\) 转换为便于存储/比较的东西(比如整数)
一般来说,我们使用多项式 Hash:\(\displaystyle f(S)=\left(\sum_{i=1}^{|S|}f(S_i)b^{|S|-i}\right)\bmod m\),其中 \(b\) 称作底数,\(m\) 称作模数,对于单个字符 \(c\),我们可以简单地将 \(f(c)\) 定义为 \(c\) 的 ASCII 码。我们一般将 \(m\) 设为质数,\(b\) 可以随便选择。
显然有 \(S=T\implies f(S)=f(T)\),它的逆否命题 \(f(S)\ne f(T)\implies S\ne T\) 也是成立的。但注意,若 \(f(S)=f(T)\),\(S\) 有可能不等于 \(T\),我们称这种情况为哈希碰撞。
定理 1.1:对于两个随机字符串 \(S,T\),它们哈希碰撞(即 \(f(S)=f(T)\) 但 \(S\ne T\))的概率为 \(\dfrac{\max(|S|,|T|)-1}{m}\)。
证明不会,可以去看 oi-wiki。
定理 1.2:对于 \(n\) 个随机字符串,它们发生哈希碰撞的概率为 \(\displaystyle 1-\prod_{i=0}^{n-1}(1-\frac{i}{m})\)。
证明还是不会/oh/oh/oh。
一般我们会选择 \(m=10^9+7\) 或 \(m=998244353\),但在 \(n=10^6\) 的情况下,错误率是极高的。所以我们一般会使用一种叫做双哈希的技巧,通过选取两个模数 \(m_1,m_2\) 分别对 \(S\) 进行 Hash,可以使值域扩大到 \(m_1m_2\),减小错误率。我一般选的是 \(m_1=10^9+7,m_2=998244353\),此时值域扩大到了约 \(10^{18}\),错误率下降到了约 \(10^{-7}\)。
\(\mathtt{1/1}\) 查询子串 Hash 值
我们可以将多项式 Hash 看成 将字符串 \(S\) 当作 \(b\) 进制数转化为 \(10\) 进制,于是理所当然的,通过维护 \(S\) 的前缀的 Hash 值 \(h_i=f(S[1,i])\),我们可以使用 \(h_r-h_{l-1}b^{r-l+1}\) 来得到 \(f(S[l,r])\),其中 \(b^{r-l+1}\) 可以简单地预处理出来。
\(S\) 的前缀的 Hash 值可以简单预处理,有 \(h_i=h_{i-1}b+f(S_i)\),边界条件为 \(h_0=0\)。
\(\mathtt{1/2}\) 字符串匹配
给定两个字符串 \(S,T\),你需要在 \(S\) 中找到所有位置 \(i\),使 \(S[i,i+|T|-1]=T\)。
朴素做法是枚举 \(i\),然后暴力判断,时间复杂度 \(\mathcal{O}(|S||T|)\)。
我们在后面会学到许多能在很优的复杂度内做字符串匹配的算法,但哈希也可以很简单地实现它。
我们先预处理出 \(S\) 的前缀 Hash 值和 \(T\) 的 Hash 值,枚举 \(i\),我们可以取出 \(S[i,i+|T|-1]\) 子串的 Hash 值,直接和 \(T\) 的 Hash 值比较即可。时间复杂度 \(\mathcal{O}(|S|+|T|)\)。
还有很多本来应使用一些专属算法但能用 Hash 乱搞弄过去的题,下文讲这些题时将提到 Hash 做法。
\(\mathtt{2}\) 自动机
自动机分确定有限状态自动机(DFA)和非确定有限状态自动机(NFA)。OI 中 DFA 要更为常见,所以本节只介绍 DFA。
你可以将 DFA 简单地看成一张带权有向图,其中顶点被称作状态,而有向边被称作转移,边权表示该转移接受的字符。状态中有一个起始状态 \(s\) 和一组接受状态集合 \(F\),每次我们可以丢进去一个字符串,从起始状态 \(s\) 开始,我们依次查看字符串中的每个字符,根据字符找到对应的转移,并转移到对应的状态。如果最后的状态在 \(F\) 中,我们称此 DFA 接受该字符串,反之亦然。
形式化的,DFA 由以下部分构成:
- 字符集 \(\Sigma\),包含此自动机允许的字符。
- 状态集 \(V\),即 DFA 中的状态集合,如果把它看成带权有向图,\(V\) 就是图上的顶点。
- 起始状态 \(s\in V\)。
- 接受状态集 \(F\subseteq V\)。
- 转移函数 \(\delta(x,c)\),接受一个状态 \(x\in V\) 和一个字符 \(c\in\Sigma\),输出为状态 \(x\) 通过字符 \(c\) 对应的转移得到的状态,如果把自动机看成带权有向图,\(\delta\) 就描述了该图的边集。特别的,如果状态 \(x\) 没有字符 \(c\) 对应的转移,我们就令 \(\delta(x,c)=\mathrm{null}\)。\(\delta(\mathrm{null},c)=\mathrm{null}\),且 \(\mathrm{null}\not\in F\)。
对于字符串 \(S\),我们从 \(s\) 开始,通过转移函数一个字符一个字符地转移,最后如果状态属于 \(F\),我们就称该自动机接受 \(S\)。
\(\mathtt{3}\) 字典树 / Trie
Trie 是一个树状自动机,它能够接受一系列字符串的所有前缀。
首先考虑只有一个字符串 \(S\) 的情况,我们可以直接让 \(s=1\),\(\delta(i,S_i)=i+1\),同时让 \(F\) 为 \(\{i\mid 1\le i\le|S|+1\}\)。那么从 \(1\) 开始,每匹配 \(S_i\) 的一位,我们都会跳到编号加一的状态,这个过程不断扩展 \(S\) 的前缀,于是每个状态都唯一对应着 \(S\) 的一个前缀。
对于多个字符串,我们可以依次按上面的流程建出一条从根挂下来的链,如果有两个字符串 \(S,T\) 在某一位相等,我们可以让 \(S,T\) 共用当前状态。
偷一张 oi-wiki 的图:

这个 Trie 接受字符串 \(\mathtt{aa},\mathtt{aba},\mathtt{ba},\mathtt{caaa},\mathtt{cab},\mathtt{cba},\mathtt{cc}\) 及其所有前缀。对应的路径为:
\[\newcommand{\mt}[1]{\mathtt{#1}} \newcommand{\t}[1]{\stackrel{\mt{#1}}{\to}} \begin{array}{c|c} \mt{aa} & 1\t{a}2\t{b}5\\ \mt{aba} & 1\t{a}2\t{b}6\t{a}11\\ \mt{ba} & 1\t{b}3\t{a}7\\ \mt{caaa} & 1\t{c}4\t{a}8\t{a}12\t{a}15\\ \mt{cab} & 1\t{c}4\t{a}8\t{b}13\\ \mt{cba} & 1\t{c}4\t{b}9\t{a}14\\ \mt{cc} & 1\t{c}4\t{c}10 \end{array} \]可以发现,如果按每一位从小到大的顺序深度优先遍历这棵 Trie,得到的字符串也是字典序从小到大依次递增的。
如果令 \(\Sigma=\{0,1\}\),我们就得到了 01 Trie,本文不会讨论其及其相关应用。
Trie 是许多 多串构造出来的自动机 的基础,而它本身也有许多应用。
\(\mathtt{4}\) KMP 与 Border
Hash 做字符串匹配自然是一个很优的算法,但它毕竟是有错误率,且有时会点名被卡的算法,我们想要一个较优时间复杂度的确定性算法。
先来看下暴力匹配时怎么被卡到 \(\mathcal{O}(|S||T|)\) 的:
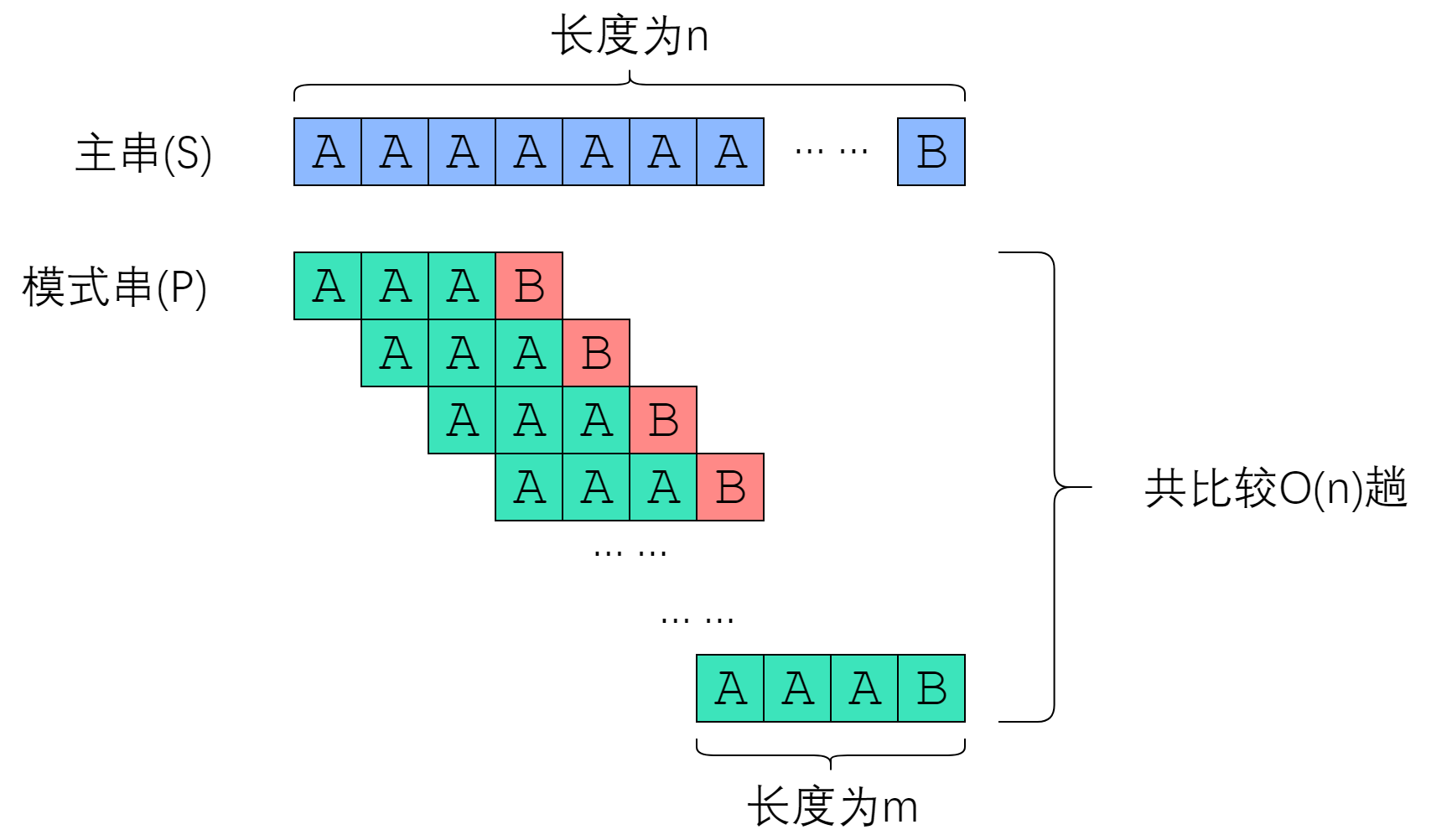
(图源 KMP 算法教程)
观察这个过程,我们实际上可以利用 \(i\) 处的匹配信息来跳过无用的段:
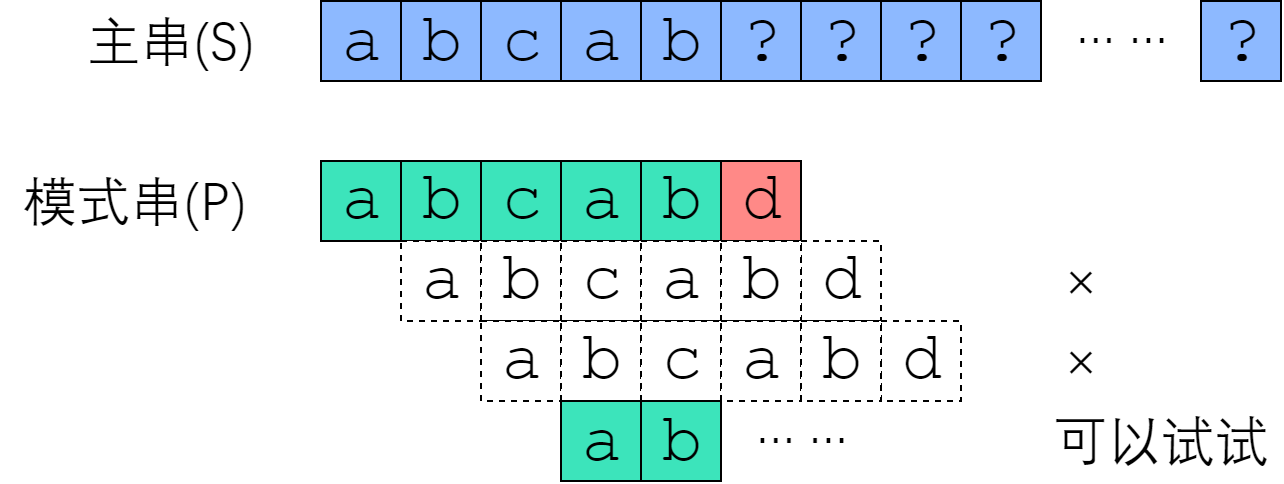
(图源 KMP 算法教程)
假设我们正在尝试从 \(S\) 的第 \(i\) 位开始匹配,如果失配在 \(T\) 的第 \(j\) 位,那么我们事实上可以利用前 \(j-1\) 位的信息。
上图中,我们从 \(S_1\) 开始匹配,在 \(T_6\) 失配,那么我们可以发现,从 \(S_2,S_3\) 开始必然失配,因为 \(S_2=T_2\ne T_1,S_3=T_3\ne T_1\)。
而 \(S_4=T_4=T_1,S_5=T_5=T_2\),所以由我们已知的信息,似乎从 \(S_4\) 开始匹配有可能能够匹配完。所以我们可以直接让 \(i\) 从 \(S_1\) 移到 \(S_4\),而且可以直接比对 \(S_6\) 和 \(T_3\),省去了大把的字符比较次数。
描述一下上面的过程:由于 \(T[1,2]=T[4,5],T[1,3]\ne T[3,5]\),所以我们可以直接将 \(i\) 从 \(S_1\) 移到 \(S_4\)。
我们引入 Border 的概念:对于一个字符串 \(S\),如果 \(S\) 的一个真子串 \(T\) 既是 \(S\) 的前缀又是 \(S\) 的后缀,我们就认为 \(T\) 是 \(S\) 的一个 Border。
举个例子:\(\mathtt{abcab}\) 的 Border 只有 \(\mathtt{ab}\)。
假设我们现在匹配到了 \(S_i\ne T_j\),失配。那么我们就需要找到最大的 \(p\) 使得 \(T[1,p]=T[j-p,j-1]\),将 \(i\) 从 \(S_i\) 退回到 \(S_{i-p}\) 和 \(T_1\) 重新匹配,又因为我们已经知道了 \(S[i-p,i-1]=T[j-p,j-1]=T[1,p]\),所以我们不用回退 \(i\),直接将 \(j\) 跳到 \(p+1\),让 \(S_i\) 和 \(T_j\) 继续比较即可。由 Border 的定义,\(p\) 就是 \(T[1,j-1]\) 的最长 Border 的长度。
注意一个特例:如果 \(j=1\),我们无法得到任何信息,只能让 \(i\) 前进一位,重新开始比较。
当我们找到一个 \(T\) 后,可以当成是在第 \(|T|+1\) 位失配进行处理。
这个过程是 \(\mathcal{O}(|S|+|T|)\) 的,我不会证。于是我们只需要快速求出 \(T\) 的前缀最长 Border 长度即可,不妨把 \(T[1,i]\) 的最长 Border 长度记作 \(p_i\)。
有 \(p_1=0\),假设我们现在已经求出了 \(p_1\) 到 \(p_{i-1}\),对于 \(p_i\),我们有两种情况:
- 若 \(T_i=T_{p_{i-1}+1}\):那么由于 \(T[1,p_{i-1}]=T[i-p_{i-1},i-1]\),自然有 \(T[1,p_{i-1}+1]=T[i-p_{i-1},i]\),显然我们不可能有更大的解(否则 \(p_{i-1}\) 也会有更大的解),所以有 \(p_i=p_{i-1}+1\)
- 若 \(T_i\ne T_{p_{i-1}+1}\):有 \(p_i\le p_{i-1}\),我们需要满足 \(T[1,p_i]=T[i-p_i+1,i]\),把此条件拆成 \(T[1,p_i-1]=T[i-p_i+1,i-1]\) 且 \(T_{p_i}=T_i\),因为 \(T[1,p_{i-1}]=T[i-p_{i-1},i-1]\) 且 \(p_i\le p_{i-1}\),于是有 \(T[i-p_i+1,i-1]=T[p_{i-1}-p_i+2,p_{i-1}]=T[1,p_i-1]\),因为 \(p_i\le p_{i-1}\),所以 \(T[1,p_i-1]\) 实际上是 \(T[1,p_{i-1}]\) 的一个 Border,我们想让 \(p_i\) 最大,于是可选的最大值即为 \(p_{p_{i-1}}\),我们判断此时的 \(T_{p_i}\) 是否等于 \(T_i\),如果等于就退出,否则重复以上流程。
复杂度是 \(\mathcal{O}(|T|)\) 的,还是不会证/ng。
于是我们就做到了 \(\mathcal{O}(|S|+|T|)\) 的字符串匹配。
\(\mathtt{5}\) AC 自动机 / Trie 图
考虑以自动机的形式理解 KMP:
我们需要实现一个自动机,使得其接受所有以给定串 \(T\) 结尾的串。
首先我们挂出一条 \(T\) 的前缀链,其上每个状态的含义为“到这个状态时,当前串以该状态对应前缀结尾”。
于是对于当前状态,如果 \(S_i\) 能够让当前状态到达下一个状态,我们可以直接转移;否则,我们需要考虑回到之前的状态。
形式化的,假设当前需要处理的字符是 \(c\),当前状态对应的前缀为 \(T[1,i]\):
- 若 \(c= T_{i+1}\),直接 \(T[1,i]\to T[1,i+1]\) 转移即可。
- 若 \(c\ne T_{i+1}\),此时我们需要找到上一个状态 \(T[1,j]\) 满足 \(T[1,j]=T[i-j+1,i]\)(即是 \(T[1,i]\) 的后缀的最长的 \(T\) 的前缀),可以发现这就是 \(p_i\),跳到上一个状态,重复此过程即可。
于是我们只需要求出 \(p_i\),在自动机中,我们不妨称其为“失配链接”。
假设我们已经求出了 \(T[1,1]\) 到 \(T[1,i-1]\) 的失配链接,现在需要求出 \(T[1,i]\) 的失配链接。考虑前一个状态 \(T[1,i-1]\),我们可以考虑在 \(T[1,i-1]\) 的失配链接 \(p_{i-1}\) 后添加 \(T_i\),如果 \(T_{p_{i-1}+1}=T_i\),那么可以直接让 \(T[1,i]\) 的失配链接指向 \(p_{i-1}+1\),否则重复这个过程,不断找到当前状态的失配链接,看能不能接上 \(T_i\) 即可。
在匹配 \(S\) 的过程中,我们不断按自动机上的边走,如果走到了接受状态 \(T[1,|T|]=T\),我们将其当作在 \(|T|+1\) 处失配,按失配逻辑跳回之前的状态继续匹配即可。
构建自动机时,我们只需要记录到下一个状态的转移和失配链接即可。
(虽然理解方式是自动机,但写出来其实和原来的几乎一样)
AC 自动机和 KMP 类似,不同的是,现在有多个模式串 \(T_1,T_2,\cdots,T_m\)(我们使用 \(T_{i,j}\) 表示 \(T_i\) 的第 \(j\) 个字符)和一个母串 \(S\),我们需要将每个 \(T_i\) 在 \(S\) 中进行匹配。
显然可以直接对每个 \(T_i\) 暴力匹配一遍,时间复杂度 \(\mathcal{O}(m|S|+\sum |T_i|)\),不优。
参考上文 KMP 在自动机意义下的理解,我们考虑将其中的一条前缀链扩展成一棵 Trie。
失配链接也不局限于单个串 \(T_i\),我们只需找到最长的那个状态满足对应的串是当前状态对应的串的后缀即可。
标签:状态,Hash,浅谈,字符串,自动机,mathtt,我们 From: https://www.cnblogs.com/bykem/p/17574260.html