$$
n^{n-2}:有标号的n个点构成的树
$$
prufer序列：https://blog.csdn.net/Code92007/article/details/106790551/
https://oi-wiki.org/graph/prufer/
建立：
过程
给一个例子吧，这是一棵 7 个结点的树的 Prüfer 序列构建过程：
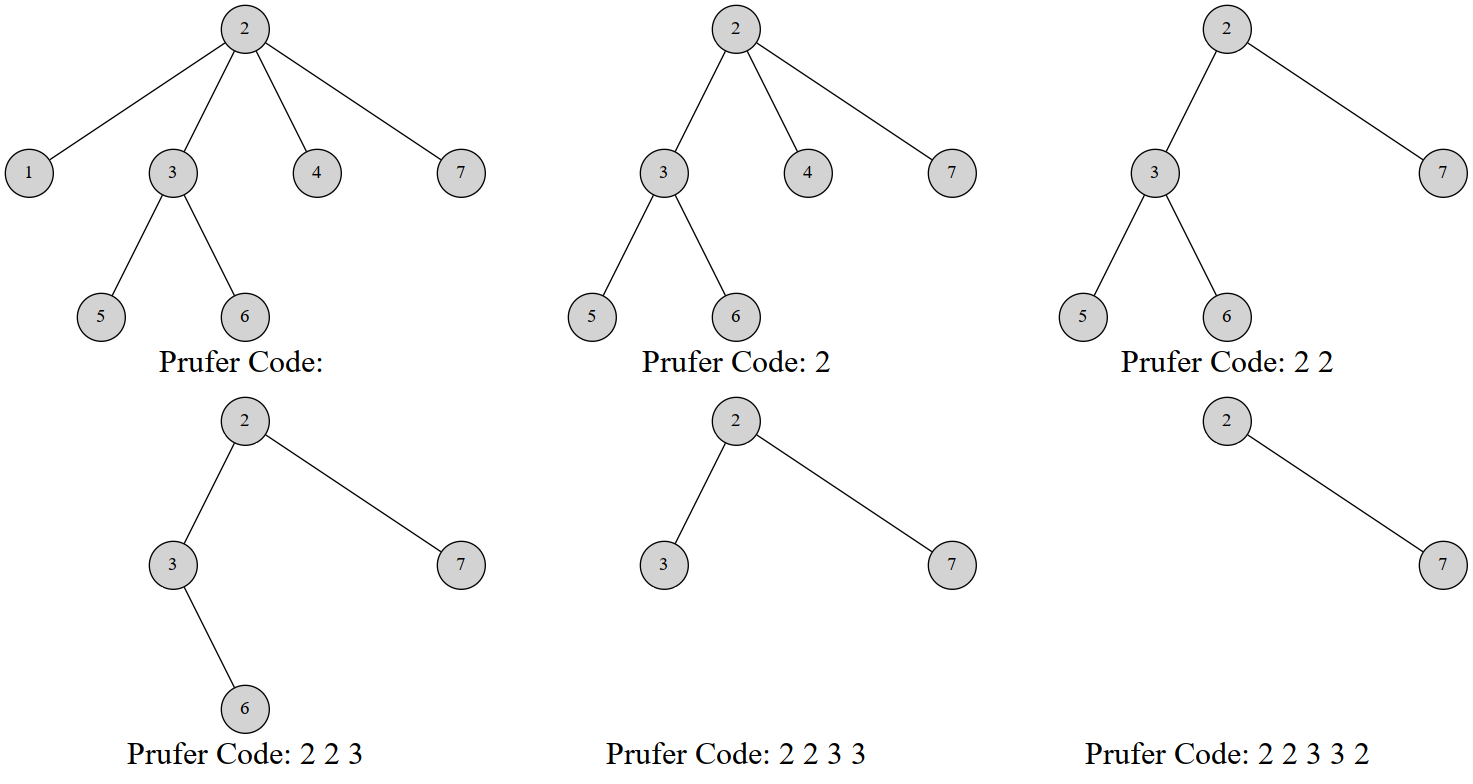
// 代码摘自原文，结点是从 0 标号的$$
vector<vector<int>> adj;
vector<int> pruefer_code() {
int n = adj.size();
set<int> leafs;
vector<int> degree(n);
vector<bool> killed(n, false);
for (int i = 0; i < n; i++) {
degree[i] = adj[i].size();
if (degree[i] == 1) leafs.insert(i);
}
vector<int> code(n - 2);
for (int i = 0; i < n - 2; i++) {
int leaf = *leafs.begin();
leafs.erase(leafs.begin());
killed[leaf] = true;
int v;
for (int u : adj[leaf])
if (!killed[u]) v = u;
code[i] = v;
if (--degree[v] == 1) leafs.insert(v);
}
return code;
}
n个点有标号的有根数计数：n^{n-2}*n=n^{n-1}
$$
线性构造
线性构造的本质就是维护一个指针指向我们将要删除的结点。首先发现，叶结点数是非严格单调递减的。要么删一个，要么删一个得一个。（翻译到这突然就知道该怎么做了，然后对照原文发现没什么问题，于是自己口糊吧）
过程
于是我们考虑这样一个过程：维护一个指针p。初始时 p
指向编号最小的叶结点。同时我们维护每个结点的度数，方便我们知道在删除结点的时侯是否产生新的叶结点。操作如下：
-
删除
p 指向的结点，并检查是否产生新的叶结点。 -
如果产生新的叶结点，假设编号为
x，我们比较 p,x 的大小关系。如果 x>p，那么不做其他操作；否则就立刻删除 x，然后检查删除 x后是否产生新的叶结点，重复 2步骤，直到未产生新节点或者新节点的编号 。 -
让指针 p
自增直到遇到一个未被删除叶结点为止；
性质
循环上述操作 次，就完成了序列的构造。接下来考虑算法的正确性。
是当前编号最小的叶结点，若删除 后未产生叶结点，我们就只能去寻找下一个叶结点；若产生了叶结点 ：
-
如果 114514 、
，则反正 往后扫描都会扫到它，于是不做操作； -
如果
，因为 原本就是编号最小的，而 比 还小，所以 就是当前编号最小的叶结点，优先删除。删除 继续这样的考虑直到没有更小的叶结点。
算法复杂度分析，发现每条边最多被访问一次（在删度数的时侯），而指针最多遍历每个结点一次，因此复杂度是 的。