首页 > 其他分享 >kruskal重构树和Prufer序列

kruskal重构树和Prufer序列

时间：2023-07-17 18:22:20浏览次数：37  
标签：重构 int kruskal fa 序列 Prufer 节点

kruskal 重构树

 首先前置知识就是 \(kruskal\) 求最小生成树，就不再多说了。

  \(kruskal\) 重构树其实就是把最小生成树这个建成一个二叉树，然后这个图中所有的叶子节点都是原图中的节点。

 其余的点每一个点都有一个权值 \(w[i]\) ，代表从左边的集合到右边的集合的路径，优于重构树是在 \(kruskal\) 的基础上完成的，所以我们必然可以得到一个自下而上点权不降的二叉树。例如这个图：

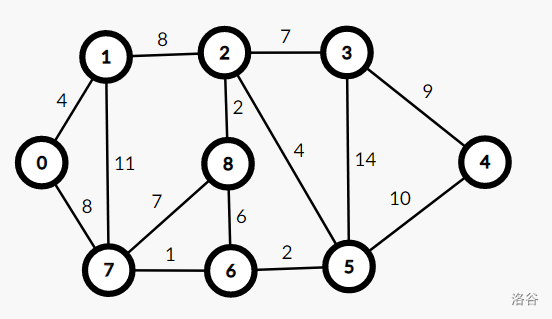
 和 \(kruskal\) 最小生成树一样，我们先按照边的边权排一个序，然后开始慢慢找，只是建树的时候不一样。

 首先我们看到 \(6 -> 7\) 这条边，我们将 \(6,7\) 放到一个并查集中去，然后建图的时候将他们两个同时连到一个新的虚点上面去，然后这个虚点的权值就是 \(1\)

 然后后面建边的时候就和这个一样建就可以了，然后两个集合连边的话连两个虚点就可以了。

 \(kruskal\) 重构树有很多独特的性质，最常用的一个应该就是求路径上最小的权值最大为多少或者路径上最大的权值最小为多少，可能还有别的用法，但是我不太清楚。

 然后求这种的时候，就先用 \(kruskal\) 跑一个最大或者最小生成树，然后求的两个点的最近公共祖先的权值就是要求的值。

 我还没有用 \(kruskal\) 重构树写过题，我都是直接硬算的（）。如果以后写了再贴吧。

Prufer序列

定义：对于一棵 \(n(n \ge 2)\) 个节点的标定树（节点带编号），其 \(Prufer\) 序列是一个长度为 \(n - 2\) ，值域为 \([1,n]\) 的整数序列。

 每棵树必存在 \(Prufer\) 序列且唯一，每个 \(Prufer\) 序列对应的树也必定存在且唯一，即两者为双射关系。

将树转化为Prufer序列

  1. 从树上选择编号最小的叶子节点，序列的下一位为其父节点的编号。

  2. 删去该叶子节点。

  3. 重复 ① 和 ② 操作，直到树只剩下两个节点，此时序列的长度刚好为 \(n - 2\) 。

一个显而易见的做法是：

 维护一个小根堆，将叶子节点依次丢入，每次从堆顶取出一个叶子节点，将其父节点的编号加入序列，然后删去该叶子节点并减小父节点的度数，如果他的父节点的度数为 \(1\) ，那么就把父节点加入小根堆，重复这个操作，执行 \(n - 2\) 次就可以求出序列了。

复杂度是：\(O(n \log n)\)

还有一种线性的做法

  1. 先找到编号最小的叶子节点，设其为 \(p\)

  2. 将 \(p\) 的父节 \(f\) 点加入序列

  3. 若删去 \(p\) 节点后，\(f\) 节点变成叶子节点，且 \(f < p\) ，那么就可以立即将 &f& 作为新选择的叶子节点进行操作。

  4. 一直执行 ③ 直到不满足条件，此时将 \(p ++\) ，直到找到下一个还没有删除的叶子节点。

总的时间复杂度为：\(O(n)\)

由Prufer序列重构树

 既然这两者是双射关系，则必然也可以由 \(Prufer\) 序列来重构一棵唯一的标定树。

 这个过程和树的序列化是十分类似的。

  1. 选择编号最小的叶子节点，即未出现在序列中的节点，其父节点就是序列的第 \(i\) （ \(i\) 初始为 \(1\) ）个元素。

  2. 由性质可得，其父节点的度数为其出现次数 \(+ 1\) 。将该叶子节点删去，其父节点度数 \(- 1\)。若度数变成 \(1\) ，那么父节点也变成叶子节点。

  3. \(i ++\) ，然后重复这操作 ① 和 ② ，直到序列的每一个元素都是用完毕。

同样，还有一种线性的方法

  1. 先找到编号最小的未出现在序列中的节点，其为叶子节点，设其为 \(p\)

  2. 将 \(p\) 的父节点 \(f\) 设为序列中尚未使用的第一个元素。

  3. 若删去节点 \(p\) 之后， \(f\) 节点变为叶子节点且 \(f < p\)，那么此时可以立即将 \(f\) 作为新选择的叶子结点进行操作。

  4. 一直执行 ③ 直到不满足条件，此时将 \(p ++\) ，直到找到下一个还没有删除的叶子节点。

最后剩下两个节点，一个必然是节点 \(n\)，将这两个节点连接即可。

应用

一般是利用于图论的组合奇数问题

1.无向完全图的不同生成树数：

 若该图有 \(n\) 个节点，则仍以一个长度为 \(n - 2\) 的 \(Prufer\) 序列都可以构造出一棵生成树，且各不相同，所以总数为 \(n ^ {n - 2}\) 。

2.\(n\) 个点，每个点度数为别为 \(d_i\) 的无根树计数：

 总排列为 \((n - 2) !\) ，即 \(A _{n - 2} ^ {n - 2}\)

 其中数字 \(i\) 出现了 \(d_i - 1\) 次，故其重复的有 \((d_i - 1) !\) 种排列，即 \(A _ {d_i - 1}^{d_i - 1}\)。

 应当 去除重复的，故总个数为 \(\frac{(n - 2)!}{\Pi _{i = 1} ^{n} (d_i - 1)!}\)

例题 P6086

int n;
int w[N],fa[N];
int d[N];

int main(){
	int type;
	n = fr(),type = fr();
	if (type == 1) {
		for (int i = 1; i < n; i ++) {
			fa[i] = fr();
			d[fa[i]] ++;
		}
		for (int i = 1,j = 1;i <= n - 2; i ++,j ++) {
			while (d[j]) j ++;
			w[i] = fa[j];
			while (i <= n - 2 && !(-- d[w[i]]) && w[i] < j) {
				w[i + 1] = fa[w[i]];
				i ++;
			}
		}
		lwl ans = 0;
		for (int i = 1; i <= n - 2; i ++) {
			ans ^= (lwl)i * w[i];
		}
		fw(ans);
	} else {
		for (int i = 1; i <= n - 2; i ++) {
			w[i] = fr();
			d[w[i]] ++;
		}
		w[n - 1] = n;
		for (int i = 1, j = 1; i < n; i++, j++) {
			while (d[j]) j ++;
			fa[j] = w[i];
			while (i < n && !(-- d[w[i]]) && w[i] < j) {
				fa[w[i]] = w[i + 1];
				i ++;
			}
		}
		lwl ans = 0;
		for (int i = 1; i < n; i ++) {
			ans ^= (lwl)i * fa[i];
		}
		fw(ans);
	}
	return 0;
}

练习

 还是图论爽啊！什么模拟什么二分什么双指针，我的评价是不如图论。前面三题都是原题，其中还有一个是今天中午刚刚做的，而且我的 \(cpp\) 文件都没有关掉。

A.电话连线（dial）

 就是比较裸的最小生成树，就是建边的时候不是直接输入的罢了。

struct node{
	int a,b,w;
	bool operator  < (const node &t) const{
		return w < t.w;
	}
}e[N];

int n,m;
int h[N];

int find(int x) {
	if (h[x] != x) h[x] = find(h[x]);
	return h[x];
}

int main(){
	n = fr();
	for (int i = 1; i <= n; i ++) {
		h[i] = i;
	}
	int idx = 0;
	for (int i = 1; i <= n; i ++) {
		for (int j = 1; j <= n; j ++) {
			int a = fr();
			if (!a) {
				h[find(i)] = find(j);
			} else {
				if (i > j) continue;
				e[++ idx] = {i,j,a};
			}
		}
	}
	int ans = 0,cnt = 0;
	sort(e + 1,e + 1 + idx);
	for (int i = 1; i <= idx; i ++) {
		int ha = find(e[i].a),hb = find(e[i].b);
		if (ha != hb) {
			cnt ++;
			ans += e[i].w;
			h[ha] = hb;
		}
	}
	fw(cnt),ch;
	fw(ans);
	return 0;
}

B.过路费

 就是上面说的 \(kruskal\) 重构树，一开始用的之前写货车运输那个写法，但总是 \(80\) 分，就直接写重构树了，还挺好用的。

struct EDGE{
	int a,b,w;
	bool operator < (const EDGE &t) const{
		return w < t.w;
	}
}edge[M];

int n,m,Q;
int h[N];
vector<int> e[N];
int de[N];
int fa[N][30];
int w[N];

int find(int x){
	if (h[x] != x)
		h[x] = find(h[x]);
	return h[x];
}

void init(int u,int p){
	de[u] = de[p] + 1;
	fa[u][0] = p;
	for (int k = 1; k <= log2(de[u]); k ++){
		fa[u][k] = fa[fa[u][k - 1]][k - 1];
	}
	for (auto &v : e[u]){
		if (v == p) continue;
		init(v,u);
	}
}

int LCA(int x,int y){
	if (de[x] < de[y])
		swap(x,y);
	
	int dh = de[x] - de[y];
	int kmax = log2(dh);
	for (int k = kmax; k >= 0; k --){
		if (dh & (1 << k)){
			x = fa[x][k];
		}
	}
	
	if (x == y) return w[x];
	
	kmax = log2(de[x]);
	for (int k = kmax; k >= 0; k --){
		if (fa[y][k] != fa[x][k]){
			x = fa[x][k];
			y = fa[y][k];
		}
	}
	
	return w[fa[x][0]];
}

signed main(){
	n = fr(), m = fr();
	int a,b,ww;
	for (int i = 1; i <= n; i ++)
		h[i] = i;
	for (int i = 1; i <= m; i ++){
		a = fr(),b = fr(),ww = fr();
		edge[i] = {a,b,ww};
	}
	
	sort(edge + 1,edge + 1 + m);
	int cnt = n;
	for (int i = 1; i <= m; i ++){
		int ha = find(edge[i].a);
		int hb = find(edge[i].b);
		if (ha != hb){
			cnt ++;
			h[ha] = cnt;
			h[hb] = cnt;
			h[cnt] = cnt;
			e[ha].push_back(cnt);
			e[cnt].push_back(ha);
			e[hb].push_back(cnt);
			e[cnt].push_back(hb);
			w[cnt] = edge[i].w;
		}
	}
	
	init(cnt,0);
	
	Q = fr();
	while (Q --){
		a = fr(),b = fr();
		int ans = LCA(a,b);
		fw(ans);
		ch;
	}
	return 0;
}

C.新的开始

 也是一个裸的 \(kruskal\) 重构树，然后用了一个虚拟点来处理前面的。

struct node{
	int a,b,w;
	bool operator < (const node &t) const{
		return w < t.w;
		
	}
}e[N * N];

int n,m;
int w[N];
int h[N];

int find(int x) {
	if (h[x] != x) h[x] = find(h[x]);
	return h[x];
}

int main(){
	n = fr();
	int idx = 0;
	for (int i = 1; i <= n; i ++) {
		w[i] = fr();
		e[++ idx] = {0,i,w[i]};
		h[i] = i;
	}
	for (int i = 1; i <= n; i ++) {
		for (int j = 1; j <= n; j ++) {
			int a = fr();
			if (i <= j) continue;
			e[++ idx] = {i,j,a};
		}
	}
	lwl ans = 0;
	sort(e + 1,e + 1 + idx);
	for (int i = 1; i <= idx; i ++) {
		int ha = find(e[i].a),hb = find(e[i].b);
		if (ha != hb) {
			h[ha] = hb;
			ans += e[i].w;
		}
	}
	fw(ans);
	return 0;
}

D.归程

 这个题是 \(kruskal\) 重构树、\(dijkstra\) 最短路还有 \(LCA\) 杂糅。

 首先先对图跑一遍 \(dijkstra\) 最短路，然后再根据每条边的海拔建 \(kruskal\) 重构树，

 然后对于每次询问来说，车能够通过的路径就是 \(a > p\) 的任意边，也就是说能通过车到达重构树的任意子树，然后再在这些子树中选出到达 \(1\) 点最短的点，然后他到 \(1\) 点的距离就是需要走的最短路径。

 然后我一开始写的时候写不出正解，就把前面的 \(45\) 分暴力给写了，本来理论上来说应该还有十分的暴力分的，但我确实是懒得打了，理论上来说那个代码应该是可以过那 \(10\) 分的树的，但是都 \(TLE\) 了，无所谓，不管了。

数组也开的不多吧，也就开了八行是不是。

struct node{
	int a,b,w,p;
	bool operator < (const node &t) const{
		return p > t.p;
	}
}e[M];

struct EDGE{
	int v,w;
};

int idx;
int n,m,p,v;
int dis[N];
int fa[N][20];
int de[N],minn[N];
int w[N],h[N];
bool flag[N];
vector<int> tr[N];
vector<EDGE> edge[N];

void dij() {
	memset(dis,0x3f,sizeof dis);
	memset(flag,0,sizeof flag);
	priority_queue<pii,vector<pii>,greater<pii> > q;
	q.push({0,1});
	dis[1] = 0;
	while (q.size()) {
		auto t = q.top();
		q.pop();
		
		int u = t.se;
		if (flag[u]) continue;
		
		for (auto &it : edge[u]) {
			if (dis[it.v] > dis[u] + it.w) {
				dis[it.v] = dis[u] + it.w;
				q.push({dis[it.v],it.v});
			}
		}
		flag[u] = true;
	}
}

int find(int x) {
	if (h[x] != x) h[x] = find(h[x]);
	return h[x];
}

void dfs(int u,int father) {
	de[u] = de[father] + 1;
	fa[u][0] = father;
	minn[u] = dis[u];
	for (int k = 1; k <= log2(de[u]); k ++) {
		fa[u][k] = fa[fa[u][k - 1]][k - 1];
	}
	for (auto &v : tr[u]) {
		if (v == father) continue;
		dfs(v,u);
		minn[u] = min(minn[u],minn[v]);
	}
}

void kruskal() {
	memset(w,0,sizeof w);
	for (int i = 1; i <= n * 2; i ++) {
		tr[i].clear();
		h[i] = i;
	}
	sort(e + 1,e + 1 + m);
	
	idx = n;
	int cnt = 0;
	for (int i = 1; i <= m; i ++) {
		int ha = find(e[i].a),hb = find(e[i].b);
		if (ha != hb) {
			cnt ++;
			h[ha] = h[hb] = ++ idx;
			w[idx] = e[i].p;
			tr[idx].push_back(ha);
			tr[idx].push_back(hb);
		}
		if (cnt == n - 1) break;
	}
}

int qurrey(int u) {
	int ans = minn[v];
	int kmax = log2(de[u]);
	for (int k = kmax; k >= 0; k --) {
		if (w[fa[u][k]] > p) {
			ans = min(ans,minn[fa[u][k]]);
			u = fa[u][k];
		}
	}
	for (auto v : tr[u]) {
		ans = min(ans,minn[v]);
	}
	return ans;
}

int main(){
	int T = fr();
	while (T --) {
		n = fr(),m = fr();
		for (int i = 1; i <= n; i ++) {
			edge[i].clear();
		}
		for (int i = 1; i <= m; i ++) {
			int a = fr(),b = fr(),ww = fr(),d = fr();
			e[i] = {a,b,ww,d};
			edge[a].push_back({b,ww});
			edge[b].push_back({a,ww});
		}
		dij();
		kruskal();
		memset(fa,0,sizeof fa);
		dfs(idx,0);
		
		int ans = 0;
		int Q = fr(),K = fr(),S = fr();
		S ++;
		while (Q --) {
			v = fr(),p = fr();
			if (K) {
				v = (v + ans - 1) % n + 1;
				p = (p + ans) % S;
			}
			ans = qurrey(v);
			fw(ans);
			ch;
		}
	}
	return 0;
}

标签：重构,int,kruskal,fa,序列,Prufer,节点
From： https://www.cnblogs.com/jingyu0929/p/17560878.html

相关文章

  • C#代码重构的几个典型案例
    前段时间小编检查同事代码，发现居然写的太复杂看不太懂，代码命名不规范，重复冗长代码一堆，这时候就可以通过重构来改进代码的质量。代码重构是提高代码质量和可维护性的关键过程，它旨在通过优化代码结构和设计来提高代码的可读性、可理解性和可扩展性。本文讲述在C#中重构代码的几个案......
  • 重构代码好方法之函数式编程
    在日常编码中，总会出现不同功能有相似之处，比如Session的连接与关闭啊，等等等等为了整理代码以获取眼睛的纯净，可以使用函数式编码步骤：重要的事说一遍第一步：定义函数式接口第二步：定义模板方法第三步：传递lambda表达式创建函数式接口@FunctionalInterfacepublicinterfaceDb......
  • 笔记-Kruskal重构树(一)
    U12讲笔记树链点权最值问题暴力：对于随机数据，单次查询平均复杂度\(O(\logn)\)目标：对于最差情况，单次查询复杂度\(O(\logn)\)倍增(\(\rmbinary\;lifting\)):预处理ST表（稀疏表）,\(\rmp[u][i]\)代表\(u\)的第\(2^i\)个祖先，\(\rmst[u][i]\)代表从\(u\)开始往上爬......
  • 单电阻采样的永磁同步电机相电流重构策略仿真，波形效果佳。
    单电阻采样的永磁同步电机相电流重构策略仿真，波形效果佳。YID:4870662310628516......
  • 主动配电网 优化调度 配电网重构 基于IEEE33节点的配电网重构，采用优化
    主动配电网优化调度配电网重构基于IEEE33节点的配电网重构，采用优化算法建模，得到重构方案，典型日联络开关的操作状态，对比了重构前后的网损和电压结果利用新型算法融合鲸鱼-布谷鸟搜索算法进行了配电网重构计算对比其他几个算法比如粒子群算法布谷鸟算法鲸鱼算法仿真结果表明......
  • 基于粒子群的配电网重构，Matlab，编程。 质量过硬，非诚勿扰
    基于粒子群的配电网重构，Matlab，编程。质量过硬，非诚勿扰！①算法：粒子群算法；②说明：以网损最小为目标，调节配网联络开关进行重构。重构后网损最小，且电压幅值满足运行要求(±7%)；③文件包括：matlab程序，visio结构图。附图为程序在IEEE33bus节点系统中的应用。ID:77210650223155431......
  • 永磁同步电机SVPWM过调制电压重构MTPA弱磁矢量控制仿真 模型 （1）内
    永磁同步电机SVPWM过调制电压重构MTPA弱磁矢量控制仿真模型（1）内置式永磁同步电机，搭建基于反馈电压环的弱磁控制MATLAB仿真模型，同时结合MTPA，使定子电流最小；（2）MTPA为公式（3）前馈解耦控制；（4）SVPWM空间矢量调制，模块包含过调制功能和电压重构功能；（5）仿真模型为产品级，附带参考资料；（6）仿真波形见截......
  • 用 AIGC 重构后的智能客服，能否淘到大模型时代的第一桶金？
    ChatGPT的诞生打响了现代AI军备竞赛的第一枪。以GPT-4、ChatGTP、Bard等为代表的大语言模型在全球各界引起了广泛关注。结合ChatGPT的底层技术逻辑，未来中短期内ChatGPT产业化的方向大致有四类：即智能客服、文字模态的AIGC应用、代码开发相关工作以及图像生成。其中，最适......
  • 代码的坏味道 《重构改善既有代码的设计》
    1.DuplicatedCode重复代码，在程序中多次出现的相同结构或功能的代码同一个类中的两个函数含有相同的表达式两个互为兄弟的子类中含相同的表达式相互独立的类中出现相同表达式2.LongMethod过长的函数难以理解及维护段函数或间接层具有很强的解释能力、共享能力和选择能......
  • Prüfer 序列
    简介Prüfer序列（以下为方便写作“prufer序列”）可以将一个带标号的\(n\)个结点的树用\([1,n]\)中的\(n-2\)个整数表示，也可以理解为完全图的生成树与数列之间的双射。定义prufer序列的简历过程为：选取树中所有叶子节点中编号最小的，将其的父节点加入序列末并删除该叶子节......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99