首页 > 其他分享 >笔记-Kruskal重构树(一)

笔记-Kruskal重构树(一)

时间：2023-07-12 15:14:46浏览次数：51  
标签：重构 int Kruskal 笔记 st fa 点权 rm 节点

U12讲笔记

树链点权最值问题

暴力：对于随机数据，单次查询平均复杂度 \(O(\log n)\)

目标：对于最差情况，单次查询复杂度 \(O(\log n)\)

倍增(\(\rm binary \; lifting\)):预处理 ST 表（稀疏表）, \(\rm p[u][i]\) 代表 \(u\) 的第 \(2^i\) 个祖先，\(\rm st[u][i]\) 代表从 \(u\) 开始往上爬的共 \(2^i\) 个节点的点权最值

注意：

  • \(\rm p[u][0]\) 是 \(u\) 的父亲
  • \(\rm st[u][0]\) 是 \(u\) 本身
  • \(\rm st[u][i]\) 不包含 \(\rm p[u][i]\)

Code

const int N=2e5+10;
vector<int> son[N];
int L,n,m,d[N],p[N][30],st[N][30];
void dfs(int u){
    d[u]=d[p[u][0]]+1;
    for(int i=1;i<=L;i++){
        p[u][i]=p[p[u][i-1]][i-1];
        st[u][i]=max(st[u][i-1],st[p[u][i-1]][i-1]);
    }
    for(int i=0;i<son[u].size();i++)
        dfs(son[u][i]);
}

int query(int u,int k){
    int ans=st[u][0];
    for(int i=0;i<=L;i++)
        if((1<<i)&k){
            ans=max(ans,st[p[u][0]][i]);
            u=p[u][i];
        }
   	return ans;
}

cin>>n>>m;
for(int u=2;u<=n;u++){
    cin>>p[u][0];
    son[p[u][0]].push_back(u);
}
for(int u=1;u<=n;u++)cin>>st[u][0];
L=log(n)/log(2)+1;
dfs(1);
for(int i=1;i<=m;i++){
    int x,k;
    cin>>x>>k;
    k=min(k,d[x]-1);
    cout<<query(x,k)<<endl;
}

KK920

最长边最短路问题

算法列举

方法1：二分答案+连通性判断

方法2：联系 MST : Kruskal 变种

推论： MST 上任意两个点之间的路径，就是它们在原图上的最长边最短路径

方法3：联系 MST : Prim 变种 / Dijkstra 变种

KK3176

题面

题目描述

有一个 \(n\) 个点 \(m\) 条边的无向连通图，边长都给定，现在有 \(K\) 个问询，格式是 \(\rm A \quad B\) ，表示从 \(A\) 号节点走到 \(B\) 号节点的所有路径中，最长的边最小值是多少。

输入格式 path.in

第一行输入三个正整数 \(n,m,k\) ，接下来 \(m\) 行，每行包含三个正整数 \(u,v,w\) 代表 \(u\) 号节点和 \(v\) 号节点之间有一条长度为 \(w\) 的边。接着 \(k\) 行问询，每行两个正整数 \(A,B\) 表示问询从 \(A\) 号节点走到 \(B\) 号节点的所有路径中，最长的边最小值是多少 。

输出格式 path.out

对于每个问询，输出一行答案，每行包含一个整数。

输入样例

6 6 8

1 2 5

2 3 4

3 4 3

1 4 8

2 5 7

4 6 2

1 2

1 3

1 4

2 3

2 4

5 1

6 2

6 1

输出样例

5

5

5

4

4

7

4

5

数据范围

算法1

利用上一题方法二的推论：

先求出 MST

然后问题转换为 MST 树上路径最大边权问询

倍增 ST 表

Code

#include<bits/stdc++.h>
using namespace std;

void dfs(int u,int fa){
    tI[u]=++timer;
    d[u]=d[fa]+1;
    p[u][0]=fa;
    st[u][0]=val[u];
    for(int i=1;i<=L;i++){
        p[u][i]=p[p[u][i-1]][i-1];
        st[u][i]=max(st[u][i-1],st[p[u][i-1]][i-1]);
    }
    for(int i=0;i<to[u].size();i++){
        int v=to[u][i];
        if(v==fa)continue;
        val[v]=w[u][i];
        dfs(v,u);
    }
    tO[u]=++timer;
}

int lca(int u,int v){
    
}

int id[N];
int root(int u){return u==id[u]?id[u]:id[u]=root(id[u]);}

int main(){
    cin>>n>>m>>k;
    for(int i=1;i<=m;i++)
        cin>>e[i].u>>e[i].v>>e[i].w;
   	sort(e+1,e+1+m,cmp);
    for(int u=1;u<=n;u++)id[u]=u;
    for(int i=1;i<=m;i++){
        int ru=root(e[i].u);
        int rv=root(e[i].v);
        if(ru==rv)continue;
        id[ru]=rv;
        to[e[i].u].push_back(e[i].v);
        to[e[i].v].push_back(e[i].u);
        w[e[i].u].push_back(e[i].w);
        w[e[i].v].push_back(e[i].w);
    }
    
    L=log(n)/log(2)+1;
    dfs(1,0);
    for(int i=1;i<=k;i++){
        int u,v;
        cin>>u>>v;
        int a=lca(u,v);
        int ans_u=0,ans_v=0;
        if(u!=a)ans_u=query(u,d[u]-d[a]-1);
        if(v!=a)ans_v=query(v,d[v]-d[a]-1);
        cout<<max(ans_u,ans_v);
    }
}

算法2-Kruskal 重构树

Kruskal 算法找 MST 时，合并操作对应二叉树

例子：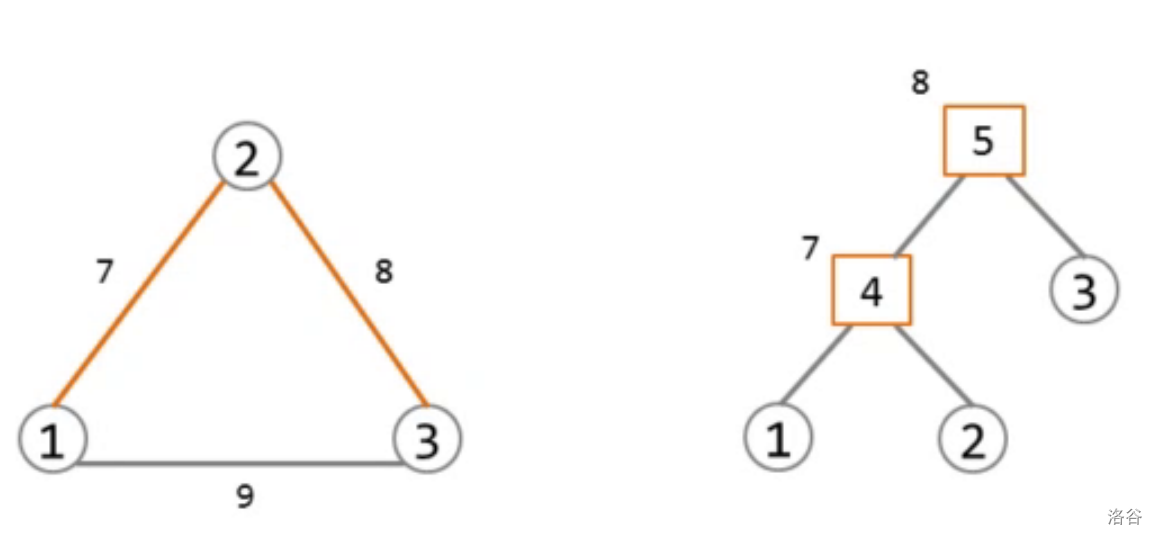

每一个附加点代表一个连通块，它的点权代表该连通块的最长边

性质：

  1. 附加点的个数一定是 \(n-1\) 个
  2. 根节点的编号一定是 \(2n-1\)
  3. 每一个附加点恰好有两个儿子
  4. 点权满足大根堆的性质(叶子没有点权，故不计在内)
  5. 原图上两点之间的最长边最短路就是新图两点间的 LCA 点权

易错点：新图的点数=原图点数*2-1

Code

void dfs(int u,int fa){
    st[u][0]=val[u];
    p[u][0]=fa;
    d[u]=d[fa]+1;
    tI[u]=++timer;
    for(int i=1;i<=L;i++){
        p[u][i]=p[p[u][i-1]][i-1];
        st[u][i]=max(st[u][i-1],st[p[u][i-1]][i-1]);
    }
    
}

int main(){
    cin>>n>>m>>k;
    for(int i=1;i<=m;i++)
        cin>>e[i].u>>e[i].v>>e[i].w;
   	sort(e+1,e+1+m,cmp);
    for(int i=1;i<=2*n-1;i++)id[i]=i;
    int nV=n;
    for(int i=1;i<=m;i++){
        int ru=root(e[i].u);
        int rv=root(e[i].v);
        if(ru==rv)continue;
        ++nV;
        id[ru]=id[rv]=nV;
        to[nV].push_back(ru);
        to[nV].push_back(rv);
        val[nV]=e[i].w;
    }
    
    L=log(n)/log(2)+1;
    dfs(nV,0);
    for(int i=1;i<=k;i++){
        int u,v;
        cin>>u>>v;
        cout<<val[lca(u,v)]<<endl;
    }
}

KK1164

题面

题目描述

有 \(n\) 座城市 \(m\) 条双向道路，每一条道路对车辆都有限重。现在有 \(q\) 辆货车在运送货物，司机们想知道每辆车在不超过限重的前提下，最多能运送多重的货物。

输入文件 truck.in

第一行包含两个整数 \(n,m\) 。接下来 \(m\) 行，每行三个整数 \(u,v,w\) 表示有一条连接 \(u\) 号城市和 \(v\) 号城市的道路限重为 \(w\) ，保证 \(u \neq v\) 但是两个城市之间可能有多条道路。接下来一行包含一个整数 \(q\), 表示有 \(q\) 个问询。接下来 \(q\) 行，每行两个整数 \(x,y\) 表示一辆货车从 \(x\) 城市到 \(y\) 城市运送货物，保证 \(x \neq y\) 。

输出文件 truck.out

输出共 \(q\) 行，每行一个整数，表示对于没一辆货车，它的最大载重是多少。如果货车不能到达目的地，输出 -1 。

输入样例

4 3

1 2 4

2 3 3

3 1 1

3

1 3

1 4

1 3

输出样例

数据范围

算法分析

易错点：

  1. 要求路径的最小边权最大化---------改排序规则
  2. 图不一定连通
  3. 有重边

Code

#include<bit/stdc++.h>
using namespace std;

void dfs(int u,int fa){
    
}

int main(){
    cin>>n>>m;
    for(int i=1;i<=m;i++)
        cin>>e[i].u>>e[i].v>>e[i].w;
    sort(e+1,e+1+m,cmp);
    for(int u=1;u<=n*2;u++)id[u]=u;
    int nV=n;
    for(int i=1;i<=m;i++){
        int ru=root(e[i].u);
        int rv=root(e[i].v);
        if(ru==rv)continue;
        ++nV;
        id[ru]=id[rv]=nV;
        to[nV].push_back(ru);
        to[nV].push_back(rv);
        val[nV]=e[i].w;
    }
    
    L=log(nV)/log(2)+1;
    for(int u=n+1;u<=nV;u++)
        if(id[u]==u)
            dfs(u,0);
    cin>>q;
    for(int i=1;i<=q;i++){
        int u,v;
        cin>>u>>v;
        int ru=root(u);
        int rv=root(v);
        if(ru==rv)
            cout<<w[lca(u,v)]<<endl;
        else
            cout<<-1<<endl;
    }
}

标签：重构,int,Kruskal,笔记,st,fa,点权,rm,节点
From： https://www.cnblogs.com/hsfzbzjr2008/p/Kruskal-chong-gou-shu-1.html

相关文章

  • 吴恩达《LangChain for LLM Application Development》课程笔记
    1.前言LangChain是一个用来构建LLM应用的开源框架，主要是为基于大语言模型的应用提供一系列的构建工具包。这个短课程的主要内容有：模型、提示和解析器：调用LLM，提供提示并解析响应。LLM的记忆：用于存储对话和管理有限上下文空间的记忆。链式操作：创建操作序列。文档问答：将LLM应用于您......
  • 4Git学习笔记
    一、Sourcetree1.使用SourceTree之前必须要先安装Git和sourceTree（gitee免费版最多可5个成员）。2.加入代码仓，需申请邀请链接。3.加入代码仓，成为的的项目开发成员之后，首先将该远程仓clone（克隆）到自己本地，作为自己的本地仓，“5-27-dq”这个仓库有两个分支，选着dev开发分支进行远程提交......
  • 5python学习笔记
    1.python特点​Python具有代码简单、学习难度低、语法清楚、功能库丰富等优势，同样功能的代码，Python代码数量只有C或Java的1/5，甚至1/10。例：打印HelloWorld，C语言需要6行，Java需要5行，Python只需要1行。2.python相关概念第三方库：需要自行安装的库python解释器：将源代码翻译......
  • 树状数组学习笔记与总结
    树状数组学习笔记与总结目录树状数组OIWiki信息学奥赛一本通例题单点修改，区间查询区间修改，单点查询区间修改，区间查询树状数组OIWikiOIWiki-树状数组信息学奥赛一本通例题单点修改，区间查询LibreOJ树状数组1：单点修改，区间查询我的代码点击查看代码#include<......
  • python学习笔记：继承与超类
    与java类似，继承的出现是为了提高代码的重复利用率，避免多次输入同样的代码。而超类就是java中的父类。1.继承要指定超类，可在定义类时，在class语句中的类名后加上超类名基类就是超类，派生类就是子类格式classDog:# passclassBobo(Dog):#Dog类的子类 pass子类会......
  • JS-Forward 学习笔记
    什么是JS-Forward?不了解的同学，可以先看看JS-Forward的Github仓库介绍，https://github.com/G-Security-Team/JS-ForwardJS-Forward是一款可以配合类似BurpSuite等抓包软件的脚本，脚本的功能是可以将js里面的参数通过Http请求将参数发送出来，在外部进行修改，最后将修改后的返回值再......
  • 组合数学 笔记
    组合数学笔寄加法原理完成一个事情有\(n\)类做法，第\(i\)类做法又分为\(a_i\)种。所以这件事情有\(S=\sum_{i=1}^{n}a_i\)的不同的完成方法。乘法原理草字头有\(3\)种写法，回字有\(4\)种写法，所以茴香豆的茴有\(S=3\times4\)种写法。同样，一件事情有\(n\)个步......
  • 【学习笔记】空空的浅谈DP
    特邀讲师：墨染空洛谷用户@Remakedalao博客中的学习笔记：https://www.cnblogs.com/dmoransky/p/14063918.htmlDP1决策单调性1.2由已知量转移：分治算法洛谷P3515：[POI2011]LightningConductor1.3由之前状态转移：单调栈上二分洛谷P1912：[NOI2009]诗人小G\(f......
  • markdown笔记
    #markdown##二级标题###三级标题####四级标题#####五级标题######六级标题#加文字加空格，一个#是一级标题，两个#是二级标题，以此类推，最多只有六级标题。菜单栏里“视图”-“大纲”，已有的标题会在大纲中显示，可以选择是否折叠显示。 ##字体**粗体***斜体****粗体加......
  • 「学习笔记」后缀数组
    感谢LB学长的博文！前置知识后缀是指从某个位置\(i\)开始到整个串末尾结束的一个特殊子串，也就是\(S[i\dots|S|-1]\)。计数排序-OIWiki(oi-wiki.org)基数排序-OIWiki(oi-wiki.org)变量后缀数组最主要的两个数组是sa和rk。sa表示将所有后缀排序后第\(i\)小......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99