目录
题目链接
原题描述
[APIO2007] 动物园
题目描述
新建的圆形动物园是亚太地区的骄傲。圆形动物园坐落于太平洋的一个小岛上,包含一大圈围栏,每个围栏里有一
种动物。如下图所示:
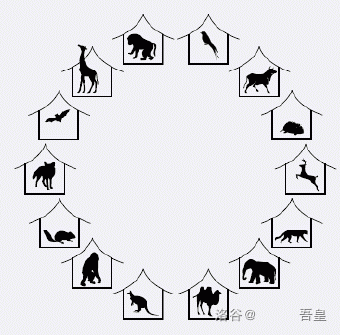
你是动物园的公共主管。你要做的是,让每个来动物园的人都尽可能高兴。今天有一群小朋友来动物园参观,你希望能让他们在动物园度过一段美好的时光。但这并不是一件容易的事——有的动物有一些小朋友喜欢,有的动物有一些小朋友害怕。如,Alex 喜欢可爱的猴子和考拉,而害怕拥牙齿锋利的狮子。而 Polly 会因狮子有美丽的鬃毛而喜欢它,但害怕有臭味的考拉。你可以选择将一些动物从围栏中移走以使得小朋友不会害怕。但你不能移走太多动物,否则小朋友们就没有动物可看了。每个小朋友站在大围栏圈的外面,可以看到连续的 \(5\) 个围栏。你得到了所有小朋友喜欢和害怕的动物信息。当下面两处情况之一发生时,小朋友就会高兴:
- 至少有一个他害怕的动物被移走
- 至少有一个他喜欢的动物没被移走
例如,考虑下图中的小朋友和动物:
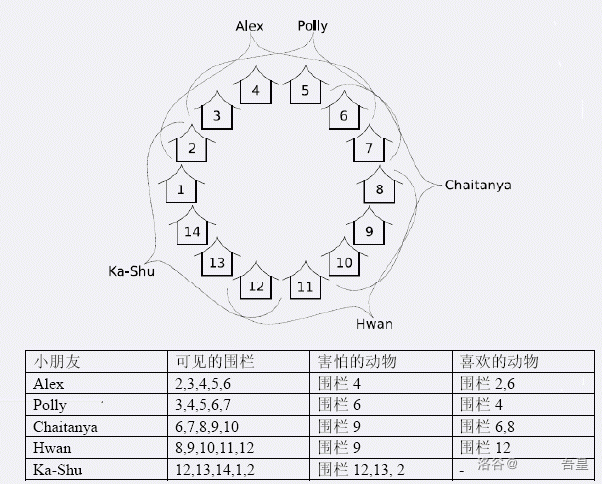
- 假如你将围栏 \(4\) 和 \(12\) 的动物移走。
Alex和Ka-Shu将很高兴,因为至少有一个他们害怕的动物被移走了。这也会使 Chaitanya 高兴,因为他喜欢的围栏 \(6\) 和 \(8\) 中的动物都保留了。但是,Polly和Hwan将不高兴,因为他们看不到任何他们喜欢的动物,而他们害怕的动物都还在。这种安排方式使得三个小朋友高兴。 - 现在,换一种方法,如果你将围栏 \(4\) 和 \(6\) 中的动物移走,
Alex和Polly将很高兴,因为他们害怕的动物被移走了。Chaitanya也会高兴,虽然他喜欢的动物 \(6\) 被移走了,他仍可以看到围栏 \(8\) 里面他喜欢的动物。同样的Hwan也会因可以看到自己喜欢的动物 \(12\) 而高兴。唯一不高兴的只有Ka-Shu。 - 如果你只移走围栏 \(13\) 中的动物,
Ka-Shu将高兴,因为有一个他害怕的动物被移走了,Alex,Polly,Chaitanya和Hwan也会高兴,因为他们都可以看到至少一个他们喜欢的动物。所以有 \(5\) 个小朋友会高兴。这种方法使得了最多的小朋友高兴。
输入格式
输入的第一行包含两个整数 \(N\),\(C\),用空格分隔。
\(N\) 是围栏数(\(10 \le N \le 10^4\)),\(C\) 是小朋友的个数(\(1 \le C \le 5\times 10^4\))。
围栏按照顺时针的方向编号为 \(1,2,3,\cdots,N\)。
接下来的 \(C\) 行,每行描述一个小朋友的信息,以下面的形式给出: \(E, F, L ,X_1, X_2 ,\cdots ,X_F ,Y_1 ,Y_2 ,\cdots ,Y_L\)。
其中: \(E\) 表示这个小朋友可以看到的第一个围栏的编号(\(1 \le E \le N\)),换句话说,该小朋友可以看到的围栏为 \(E\), \(E+1\), \(E+2\), \(E+3\), \(E+4\)。
注意,如果编号超过 \(N\) 将继续从 \(1\) 开始算。
如:当 \(N=14\),$ E=13$ 时,这个小朋友可以看到的围栏为 \(13,14,1, 2\) 和 \(3\)。
\(F\) 表示该小朋友害怕的动物数。
\(L\) 表示该小朋友喜欢的动物数。
围栏 \(X_1, X_2, \cdots, X_F\) 中包含该小朋友害怕的动物。
围栏 \(Y_1, Y_2, \cdots, Y_L\) 中包含该小朋友喜欢的动物。
\(X_1, X_2, \cdots, X_F, Y_1, Y_2, \cdots, Y_L\) 是两两不同的整数,而且所表示的围栏都是该小朋友可以看到的。
小朋友已经按照他们可以看到的第一个围栏的编号从小到大的顺序排好了(这样最小的 \(E\) 对应的小朋友排在第一个,最大的 \(E\) 对应的小朋友排在最后一个)。
注意可能有多于一个小朋友对应的 \(E\) 是相同的。
输出格式
仅输出一个数,表示最多可以让多少个小朋友高兴。
样例 #1
样例输入 #1
14 5
2 1 2 4 2 6
3 1 1 6 4
6 1 2 9 6 8
8 1 1 9 12
12 3 0 12 13 2
样例输出 #1
5
样例 #2
样例输入 #2
12 7
1 1 1 1 5
5 1 1 5 7
5 0 3 5 7 9
7 1 1 7 9
9 1 1 9 11
9 3 0 9 11 1
11 1 1 11 1
样例输出 #2
6
提示
数据范围
对于 \(100\%\) 的数据,\(10 \le N \le 10^4\),\(1 \le C \le 5\times 10^4\),\(1 \le E \le N\)。
样例说明
- 第一个样例是题目描述中的例子,所有的 \(C=5\) 个小朋友都能高兴。
- 第二个样例是一个不能使得所有 \(C=7\) 个小朋友都高兴的例子。
题意概括
给出一个点数为\(N\)的环,以及\(C\)个长度为\(5\)的连续区间,每个区间包含在该区间内不该存在的点和应该存在的点这些要求,只要满足该区间内有一个不该存在的点不存在和该存在的点存在就叫满足该区间要求,要求求出最多可以满足多少个区间的要求。
思路历程
私货:想和Miku一起去动物园看熊猫(
1.与环相关
处理环,如果我没记错的话,应该是在并查集里面做过一个题,当时的处理方法是扩展二倍数组,使其成为链。
(ps:当然这个题不是这样的)
所以说,先不管环,先把链抽出来。
2.设计状态
根据题目概括,我们发现,题目描述中的“移动”是迷惑人的,我们一开始设计的就是最后的状态,与其说是“移动”,不如说是“选点”。
而状态,和题目旅游景点 Tourist Attractions显然是相似的,不是针对限制条件设置状态,而是在状态转移时满足限制。
(ps:其实都是这样的吧起码我做的题是这样的,但是本人是蒟蒻没做几道题捏)
那么我们的状态就很明显:\(f_{j,s}\)表示表示\([1,j]\)区间内,\([j,j+4]\)的状态为s时,最多可以符合多少个区间的条件
\(satisfy_{i,s}\)表示区间范围为\([i,i+4]\)、状态为\(s\)时,能够满足的区间数。
\[\begin{aligned} f_{j,s}=max(f_{j-1,s去掉第第j+4个点并右移一位,第1位是0},f_{j-1,s去掉第j+4个点并右移一位,第一位是1})+satisfy_{j,s} \end{aligned} \]呃呃如果看不懂就看一下代码注释:
码代码慢慢悟(
代码实现
Miku's Code
#include<bits/stdc++.h>
using namespace std;
typedef long long intx;
const int maxn=1e4+50,maxc=5e4+50;
#define fs 31
#define ms 16
#define ss 30
/*
fs=31表示状态1 1 1 1 1
ms=16表示状态1 0 0 0 0
ss=30表示状态1 1 1 1 0
*/
int N,C;
int st[maxc],fright[maxc],favor[maxc];
int fri,fav;
int ans;
//输入相关
int satisfy[maxc][fs+5];
//satisfy[i][s]表示区间范围为[i,i+4]、状态为s时,能够满足的区间数
int f[maxn][fs+5];
//f[j][s]表示[1,j]区间内,[j,j+4]的状态为s时,最多可以符合多少个区间的条件
inline void input(){ //输入并预处理
int fear,like;
scanf("%d %d",&N,&C);
for(int i=1;i<=C;++i){
fear=0;like=0;
scanf("%d %d %d",&st[i],&fright[i],&favor[i]);
for(int j=1;j<=fright[i];++j){
scanf("%d",&fri);
fri=(fri-st[i]+N)%N;
/*
fri表示区间i不该存在的点j在其区间的(第几个位置-1)
因为我们是在区间[st[i],st[i]+4]中设计状态,所以应该转换成其区间的相对位置
因为是环,所以(+N)%N防止负数
*/
fear=fear|(ms>>fri);
/*
我们对fri预处理是从左到右的,因此我们的状态与其保持一致的方向
ms在第一位是1,左移fri位置
这样我们就得了应该存在的点的状态fear
*/
}
for(int j=1;j<=favor[i];++j){
scanf("%d",&fav);
fav=(fav-st[i]+N)%N;
like=like|(ms>>fav);
//同上
}
for(int j=0;j<=fs;++j){
if((fear&(~j)) || (like&j)){
++satisfy[st[i]][j];
}
}
}
}
inline void work(){
for(int i=0;i<=fs;++i){
memset(f[0],128,sizeof(f[0]));
//128是一个负数极小值
f[0][i]=0;
for(int j=1;j<=N;++j){
for(int s=0;s<=fs;++s){
f[j][s]=max(f[j-1][(s&ss)>>1],f[j-1][((s&ss)>>1)+ms])+satisfy[j][s];
/*
(s&ss)>>1表示[j-1,j+3]的状态,j-1位置为0
((s&ss)>>1)+ms则表示j-1位置为1
[1,j]=max([1,j-1])+satisfy[j]
*/
}
}
if(ans<f[N][i]){
ans=f[N][i];
//最初状态为i,最后状态也为i
}
}
}
int main(){
input();
work();
printf("%d\n",ans);
return 0;
}