前情提要:前些日子看Clover_BY操前看了蓝书上的一道题:(我操前一直什么也不带)
有 \(N\) 个学生合影,站成左端对齐的 \(k\) 排,每排分别有 \(N_1,N_2,\cdots,N_k\) 个人,第一排站在最后面,第 \(k\) 排站在最前面。学生的身高互不相同,把他们从高到低依次标记为 \(1,2,\cdots,N\) 。在合影时要求每一排从左到右身高递减,每一列从后到前身高也递减,问一共有多少种安排合影位置的方案。
(实际上这个题的 \(N\) 是单调递减的)
然后当时就发现了杨表不会的事实。然后当天就补了一发。
杨表是一种精妙的组合结构生成函数的白给。(不知道为什么我bdfs一下一堆杨表的插入元素删除元素的,真的有人会拿杨表维护什么东西吗)
首先是一些别的(长得很像的)东西:Ferrers图(或者叫杨图)。
\[\begin{aligned} &5:\blacksquare\ \blacksquare\ \blacksquare\ \blacksquare\ \blacksquare\\ &4:\blacksquare\ \blacksquare\ \blacksquare\ \blacksquare\\ &2:\blacksquare\ \blacksquare\\ &1:\blacksquare\\ &1:\blacksquare \end{aligned} \]可以描绘一个整数分拆。或者换成表格的形式:

整数分拆当然也有许多的优美性质,但是限于篇幅,将会另开一栏专门解释。我们今天的主角不是什么整数分拆。
杨表
杨表(Young tableau)是通过用取自某个字母表的符号填充杨氏图的框来获得的,这通常需要是一个全序集和。填入的元素写作 \(x_1,x_2,x_3,\cdots\)。但为了方便起见,都直接填入正整数。(摘自oi-wiki)
这里我们只讨论标准杨表:用 \(1-n\) 共 \(n\) 个互不相同的正整数填满整个表,并满足各行各列的数字都严格递增。
对于 \(n\) 个方格的标准杨表个数,我们有递推式:
\[f(0)=1,f(1)=1\\ f(n)=f(n-1)+(n-1)\times f(n-2) \]等于 \(n\) 个点完全图的匹配方案数。前几项是:
\[1,1,2,4,10,26,76,232,764,2620,9496,\cdots \]还有一种半标准的杨表:可以填入相同数字,列严格递增,行单调不降,则为半标准杨表(这个实际上可以计数,一会说)。
标准杨表的插入算法
对于标准杨表,我们有将一个元素插入它的算法:RSK插入算法。同时,这提供了一个将杨表和排列联系起来的途径。它的步骤是(如果我们要插入 \(x\) ):
- 从第一行开始,在当前行中找到最小的比 \(x\) 大的数 \(y\) 。
- 如果找到,用 \(x\) 替换 \(y\) ,移动到下一行继续插入 \(y\) 。
- 如果没有找到,直接放在该行末尾。
上图:




删除同理。我们如果删除 \(x\) ,则在上一行找到最大的比 \(x\) 小的数,用 \(x\) 替换,移动到上一行继续删除。
然后我们可以用这个算法往杨表里插入一个排列,同时记录一个表,当第 \(i\) 次在某个格子填上数的时候将另一个表的这个格子填上 \(i\) ,那么最后这两个杨表的形态是一样的。也就是说,两个大小为 \(n\) 的杨表对应一个长度为 \(n\) 的排列。也就是说,我们有如下公式(Robinson-Schensted correspondence
定理):
其中 \(\lambda⊢n\) 是 \(n\) 的一个整数拆分, \(f_{\lambda}\) 是这种拆分在杨表的填法数。
然后关于这个填法数怎么求,我们还有一个公式。
勾长公式
对于杨表的一个方格 \(v\) 定义其勾长 \(\text{hook}(v)\) 为其同行右边的方格数加上同列下面的方格数,然后再加上自己。
然后我们有勾长公式:一个杨表的填法数等于 \(n!\) 除以所有方格勾长的乘积。
\[f_{\lambda}=\frac {n!}{\prod_x \text{hook}(x)} \]所以上面这张杨表的填法数为: \(\frac{10!}{7\times 5\times4\times3\times1\times5\times3\times2\times1\times1}=288\) 。
于是我们可以通过暴力扫来求勾长。需要用到另一个形式:
\[f_{\lambda}=n!\frac{\prod_{1\le i<j\le m}(\lambda_i-i-\lambda_j+j)}{\prod_{i=1}^m(\lambda_i+m-i)!} \]int solve(){
int ret=1;
for(int i=1;i<=a[0];i++){
for(int j=i+1;j<=a[0];j++)ret=1ll*ret*(a[i]-i-a[j]+j+mod)%mod;
}
for(int i=1;i<=a[0];i++)ret=1ll*ret*inv[a[i]+a[0]-i]%mod;
ret=1ll*ret*jc[n]%mod;
return ret;
}
然后事实上这个可以多项式乘法实现一个 \(\log\) 的复杂度计算。我们再变形一下:设 \(r_i=a_i+m-i\) ,那么 \(f_{\lambda}=n!\frac{\prod_{1\le i<j\le m}(r_i-r_j)}{\prod_{i=1}^mr_i}\) 。用一个数组记录 \(r_i\) 出现的次数( \(r\) 显然互不相同),如果出现了就记录 \(c_r=1\) ,没有就是 \(0\) 。然后多项式卷积算出 \(g_k=\sum_{i-j=k}c_ic_j\) ,上面的 \(\prod_{1\le i<j\le m}(r_i-r_j)\) 就是 \(\prod_{i=1}^ni^{g_i}\) 。代码在此不表。怎么暴力怎么算就行。
然后是杨表的一些结论:
- 杨表第一行的长度就是它对应排列的LIS长度(不一定是排列的LIS)。
- 杨表第一列的长度是这个排列的LDS(最长下降子序列)长度。
- 对一个排列和它的杨表,这个排列倒过来的杨表就是这个杨表的转置。
- 元素比较方式取反,则杨表的形状转置(元素不一定)。
- 定义一个序列的 \(k-\text{LIS}\) 为这个序列的最长的满足LIS长度不超过 \(k\) 的子序列。那么它的长度就是这个序列对应杨表的前 \(k\) 列长度和。
然后我们可以来水一道题:BJWC2018 最长上升子序列。
题意:求 \(n\) 长度排列的LIS期望长度 \(\mod 998244353\) 。
根据上面的公式,我们知道答案就是
\[\frac 1{n!}\sum_{\lambda⊢n}f_{\lambda}^2\lambda_1 \]暴力枚举整数拆分即可。跑 \(60\) 只需要 \(0.6\text s\) 。
#include <algorithm>
#include <iostream>
#include <cstdio>
using namespace std;
const int mod=998244353;
int n,ans,a[30],jc[30],inv[30];
int qpow(int a,int b){
int ans=1;
while(b){
if(b&1)ans=1ll*ans*a%mod;
a=1ll*a*a%mod;
b>>=1;
}
return ans;
}
int solve(){
int ret=1;
for(int i=1;i<=a[0];i++){
for(int j=i+1;j<=a[0];j++)ret=1ll*ret*(a[i]-i-a[j]+j+mod)%mod;
}
for(int i=1;i<=a[0];i++)ret=1ll*ret*inv[a[i]+a[0]-i]%mod;
ret=1ll*ret*jc[n]%mod;
return ret;
}
void dfs(int x,int mx){
if(x==0){
int ret=solve();
ans=(ans+1ll*ret*ret%mod*a[1]%mod)%mod;
return;
}
for(int i=min(x,mx);i>=1;i--){
a[++a[0]]=i;
dfs(x-i,i);
a[0]--;
}
}
int main(){
scanf("%d",&n);jc[0]=inv[0]=1;
for(int i=1;i<=n;i++){
jc[i]=1ll*jc[i-1]*i%mod;
inv[i]=qpow(jc[i],mod-2);
}
dfs(n,n);
printf("%lld\n",1ll*ans*inv[n]%mod);
}
CTSC2017 最长上升子序列
题意:给你一个序列,多次询问,每次求它前 \(m\) 个元素的 \(k-\text{LIS}\) 。
首先显然将询问离线排序然后逐个插入元素回答询问。
据说这个题暴力维护前缀的杨表可以得到 \(95\) 分。然后发现暴力维护的话单次查询最坏是 \(O(n\log n)\) 的,考虑优化。
显然杨表行和列最小的一维长度不会超过 \(\sqrt n\) ,于是我们只需要维护前 \(\sqrt n\) 行和列,如果列数大于 \(\sqrt n\) 就把比较方式取反,维护这个杨表的转置就行了,总复杂度 \(O(n\sqrt n\log n)\) 。
代码比较简明。
#include <algorithm>
#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
int n,Q,sq,c[50010],ans[200010],a[50010];
int lowbit(int x){
return x&-x;
}
void update(int x,int val){
while(x<=n)c[x]+=val,x+=lowbit(x);
}
int query(int x){
int sum=0;
while(x)sum+=c[x],x-=lowbit(x);
return sum;
}
struct Young{
int a[310][50010];
void ins(int x,int val,int id){
if(x>sq)return;//只维护根号以内的
int l=1,r=a[x][0]+1;
while(l<r){
int mid=(l+r)>>1;
if(id^(val<=a[x][mid]))r=mid;
else l=mid+1;
}//二分第一个大于val的值
swap(a[x][l],val);
a[x][0]=max(a[x][0],l);//交换,更新大小
if(val)ins(x+1,val,id);
else{
if(id)update(x,1);//直接更新上去
else if(l>sq)update(l,1);//如果超过根号说明另一个没法维护 上树状数组
}
}
}a1,a2;
struct ques{
int m,k,id;
bool operator<(const ques &s)const{
return m<s.m;
}
}q[200010];
int main(){
scanf("%d%d",&n,&Q);
sq=sqrt(n);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<=Q;i++){
scanf("%d%d",&q[i].m,&q[i].k);q[i].id=i;
}
sort(q+1,q+Q+1);
int pos=0;
for(int i=1;i<=Q;i++){
while(pos<q[i].m){
pos++;
a1.ins(1,a[pos],0);a2.ins(1,a[pos],1);
}
ans[q[i].id]=query(q[i].k);
}
for(int i=1;i<=Q;i++)printf("%d\n",ans[i]);
}
随机游走:见这篇博客。
斜杨表
斜杨表就是一个大杨表砍掉一个小杨表。大概长成这样:
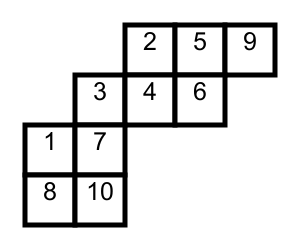
大的为 \(\lambda\) ,小的为 \(\mu\) 的话,这玩意记作 \(\lambda/\mu\) 。
然后是斜半标准杨表计数。一个 \(m\) 行,值域 \([1,z]\) 的斜半标准杨表可以表示为 \(m\) 条 \((\mu_i-i,1)\rightarrow(\lambda_i,z)\) 的不相交路径。如图:

使用LGV引理好像可以解决。
半标准杨表计数
直接上公式(完全不会证明):( \(h_{\lambda}(i,j)\) 是这个整数拆分对应杨表坐标 \((i,j)\) 的勾长)
\[f_{\lambda}'=\prod_{_i,j\in \lambda}\frac{n+j-i}{h_{\lambda}(i,j)}=\prod_{1\le i<j\le m}\frac{\lambda_i-i-\lambda_j+j}{j-i} \]又一个二百多行的数学博客。格路计数还是不会。
标签:int,blacksquare,杨表,长度,include,lambda From: https://www.cnblogs.com/gtm1514/p/16737209.html