问题描述
1595. 连通两组点的最小成本 (Hard)
给你两组点,其中第一组中有 size₁ 个点,第二组中有 size₂ 个点,且 size₁ >= size₂ 。
任意两点间的连接成本 cost 由大小为 size₁ x size₂ 矩阵给出,其中 cost[i][j] 是第一组中的点 i
和第二组中的点 j 的连接成本。 如果两个组中的每个点都与另一组中的一个或多个点连接,则称这两组点是
连通的。 换言之,第一组中的每个点必须至少与第二组中的一个点连接,且第二组中的每个点必须至少与第一
组中的一个点连接。
返回连通两组点所需的最小成本。
示例 1:
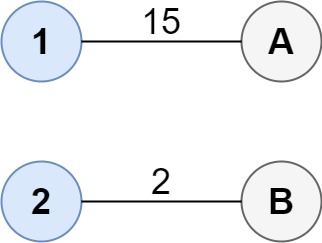
输入:cost = [[15, 96], [36, 2]]
输出:17
解释:连通两组点的最佳方法是:
1--A
2--B
总成本为 17 。
示例 2:
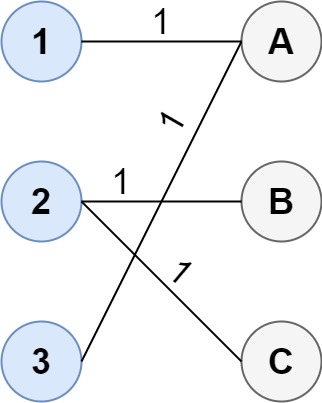
输入:cost = [[1, 3, 5], [4, 1, 1], [1, 5, 3]]
输出:4
解释:连通两组点的最佳方法是:
1--A
2--B
2--C
3--A
最小成本为 4 。
请注意,虽然有多个点连接到第一组中的点 2 和第二组中的点 A ,但由于题目并不限制连接点的数目,所以只需
要关心最低总成本。
示例 3:
输入:cost = [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8]]
输出:10
提示:
size₁ == cost.lengthsize₂ == cost[i].length1 <= size₁, size₂ <= 12size₁ >= size₂0 <= cost[i][j] <= 100
解题思路
动态规划 + 状态压缩
我们用二进制数 $j$ 表示对第二组选择的元素的集合,dp[i][j] 表示对第一组的前 $i$ 个数组成的的集合,以及第二组中元素的集合 $j$,这两个集合的最小联通成本。
那么如何思考递推关系呢,对第一组的元素,我们考虑第 $i$ 个元素,同时枚举集合中的元素 $k$,($k$ 表示元素索引),那么有以下几种情况:
- 第 $i$ 个元素只与 $k$ 相连,那么可以分两种情况:
- 第二组索引为 $k$ 的元素只与第 $i$ 个元素相连:$dp[i][j] = min(dp[i][j], dp[i - 1][j\oplus(1 << k)] + cost[i - 1][k])$;
- 第二组索引为 $k$ 的元素不只与第 $i$ 个元素相连:$dp[i][j] = min(dp[i][j], dp[i - 1][j] + cost[i - 1][k])$;
- 第 $i$ 个元素不只与 $k$ 相连,那么可以再分两种情况。
- 第二组的索引为 $k$ 的元素只与第 $i$ 个元素相连:$dp[i][j] = min(dp[i][j], dp[i][j\oplus (1 << k)] + cost[i - 1][k])$;
- 第二组的索引为 $k$ 的元素与除了第 $i$ 个元素之外的其他元素也相连,那么这时候第 $i$ 个元素不需要与索引为 $k$ 的元素相连了,因此不用考虑,假设强行连接第 $i$ 个元素和元素 $k$,那么必然会出现多余的边,去掉多余的边,则情况变成了枚举 $k_1$ 或者 $k$ 或者 $k2$ 的上述三种情况了。
注意每次枚举 $k$ 时,都要与之前计算过的 $dp[i][j]$ 进行比较!同时 for 循环中一旦出现不满足判断条件了情况,就会终止循环了!
代码
class Solution {
public:
int connectTwoGroups(vector<vector<int>> &cost) {
int m = cost.size(), n = cost[0].size();
vector<vector<int>> dp(m + 1, vector<int>(1 << n, INT_MAX));
dp[0][0] = 0;
// dp[i][j] 表示前 i 个点与集合 j 的最小值
// 对点 i - 1,枚举集合 j 中的点 k,如果 k 只与点 i - 1 相连,dp[i][j] = dp[i][j\k] + cost[i - 1][k];
// 如果点 i - 1 只与 k 相连,那么 dp[i][j] = min(dp[i - 1][j\k], dp[i - 1][j]) + cost[i - 1][k]
for (int i = 1; i <= m; ++i) {
for (int j = 1; j < (1 << n); ++j) {
for (int k = 0; (1 << k) <= j; ++k) {
if (((1 << k) & j) == 0) {
continue;
}
int tmp = min(dp[i][j ^ (1 << k)], min(dp[i - 1][j ^ (1 << k)], dp[i - 1][j])) + cost[i - 1][k];
dp[i][j] = min(tmp, dp[i][j]);
}
}
}
return dp[m][(1 << n) - 1];
}
};