将地理坐标系进行投影后,即得到投影坐标系。最常用的适用于我国的地图有以下几种:
- 高斯克吕格(Gauss Kruger)投影
是以椭圆柱为投影面,使地球椭球体的某一经线与椭圆柱相切,然后按等角条件,将中央经线两侧各一定范围内的经纬线投影到椭圆柱面上,再将其展成平面而得。
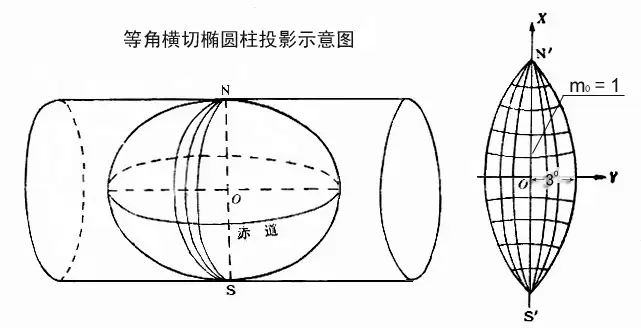
2、通用横轴墨卡托(Universal Transverse Mercator, UTM)投影
其实质是等角横割圆柱投影,它是以圆柱为投影面,使圆柱割于地球椭球体的两条等高圈上,然后按等角条件,将中央经线两侧各一定范围内的经纬线投影到圆柱面上,再将其展成平面而得。

UTM投影和高斯克吕格投影的区别:
(1)中央经线长度比不同,UTM投影是0.9996,而高斯-克吕格投影是1。
(2)带的划分相同,而带号的起算不同。
(3)对于中、低纬度地区,UTM投影的变形优于高斯-克吕格投影。
(4)西方国家(美、英、德、法)多采用UTM投影作为国家基本地形图投影,东方国家(中、苏、蒙、朝)多采用高斯-克吕格投影作为国家基本地形图投影。
标签:克吕格,高斯,中央经线,Universal,投影,UTM,椭圆柱 From: https://www.cnblogs.com/yibeimingyue/p/17486658.html