贪心算法

概述

贪心算法总是做出 当前最好 的选择，期望通过 局部最优 选择得到 全局最优 的解决方案。贪心算法正是“活在当下，看清楚眼前”的算法，从问题的 初始解 开始，一步步地做出当前最好的选择，逐步逼近问题的目标，尽可能得到 最优解 ；即使得不到最优解，也可以得到最优解的 近似解 .

贪心算法并 不是从整体最优来考虑的 ，它所作出的选择只是某种意义上的 局部最优 。对许多问题可以使用贪心算法得到整体最优解或整体最优解的近似解。

本质

可以使用贪心算法的情况：问题具有两个特征—— 贪心选择性质 和 最优子结构性质 。

1. 贪心选择性质
   贪心选择性质指原问题的 整体最优解 可以通过 一系列 局部最优 的选择得到。应用 同一规则 ，将原问题变为一个 相似的、但规模更小的 子问题，而后的每一步都是 当前最优 的选择。这种选择依赖于 已做出 的选择，但不依赖于未做出的选择。运用贪心算法解决的问题在程序运行过程中 无回溯 过程。
2. 最优子结构性质
   当一个问题的最优解 包含 其 子问题的最优解 时，称此问题具有 最优子结构性质 。问题的 最优子结构性质 是该问题是否可以用贪心算法求解的 关键 。 例如： 原问题$ S = {a_1,a_2,…,a_i,…,a_n} $，通过贪心选择出一个当前最优解 $ {a_i}$ 之后，转化为求解子问题 $ S - {a_i} $ ，如果原问题的最优解包含子问题的最优解，则说明该问题满足最优子结构性质。

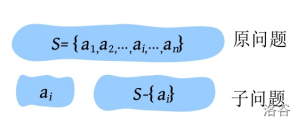
贪心算法的 求解步骤 如下。

（1） 贪心策略 。指确定贪心策略，选择 当前看上去最好的一个 。 比如： 挑选苹果，如果你认为 个头大 的是最好的，那么每次都从苹果堆中拿一个 最大的 作为 局部最优解 ，贪心策略就是选择当前 最大的苹果 。如果你认为 最红的 苹果是最好的，那么每次都从苹果堆中拿一个 最红的 ，贪心策略就是选择当前 最红的苹果 。因此根据求解目标的不同，贪心策略也会不同。

（2） 局部最优解 。指根据贪心策略，一步步地 得到局部最优解 。比如第1次选一个最大的苹果放起来，记为 \(a_1\) ；第2次再从剩下的苹果中选择一个最大的苹果放起来，记为 \(a_2\) ，以此类推。

（3） 全局最优解 。指把所有的局部最优解都合成原问题的一个最优解 \(\{a_1,a_2……\}\) 。