1020.飞地的数量 (Medium)

问题描述

1020. 飞地的数量 (Medium)

给你一个大小为 m x n 的二进制矩阵 grid ，其中 0 表示一个海洋单元格、 1 表示一个陆地单元格。

一次 移动 是指从一个陆地单元格走到另一个相邻（ 上、下、左、右）的陆地单元格或跨过 grid 的边界。

返回网格中 无法 在任意次数的移动中离开网格边界的陆地单元格的数量。

示例 1：

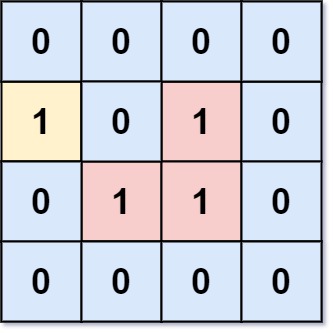
输入：grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
输出：3
解释：有三个 1 被 0 包围。一个 1 没有被包围，因为它在边界上。

示例 2：

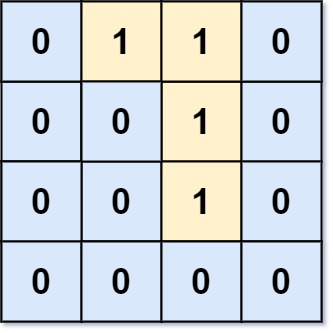
输入：grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
输出：0
解释：所有 1 都在边界上或可以到达边界。

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 500
• grid[i][j] 的值为 0 或 1

解题思路

使用并查集，令cnt1为包含索引为m * n的节点树的节点数，cnt2为海水的节点数，res = m * n - (cnt1 - 1) - cnt2;。

代码

struct Dsu {
    vector<int> par_;
    vector<int> siz_;
    int cnt_;
    explicit Dsu(int cnt) :
        par_(cnt + 1), siz_(cnt + 1, 1), cnt_(cnt) {
        for (int i = 0; i <= cnt; ++i) {
            par_[i] = i;
        }
    };
    auto find(int x) -> int {
        return par_[x] == x ? x : (par_[x] = find(par_[x]));
    }
    void uni(int x, int y) {
        x = find(x), y = find(y);
        if (x == y) {
            return;
        }
        if (siz_[x] < siz_[y]) {
            std::swap(x, y);
        }
        par_[y] = x;
        siz_[x] += siz_[y];
        --cnt_;
    }
};
class Solution {
  public:
    int numEnclaves(vector<vector<int>> &grid) {
        // 并查集
        int m = grid.size(), n = grid[0].size();
        vector<vector<int>> move{{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
        Dsu dsu(m * n);
        int cnt = 0;
        for (int i = 0; i < m * n; ++i) {
            int x = i / n, y = i % n;
            if (grid[x][y] == 1) {
                if (x == m - 1 || x == 0 || y == 0 || y == n - 1) {
                    dsu.uni(i, m * n);
                }
                for (int j = 0; j < 4; ++j) {
                    int x_new = x + move[j][0], y_new = y + move[j][1];
                    if (x_new < 0 || x_new >= m || y_new < 0 || y_new >= n || grid[x_new][y_new] == 0) {
                        continue;
                    }
                    dsu.uni(i, x_new * n + y_new);
                }
            } else {
                ++cnt;
            }
        }
        return m * n - dsu.siz_[dsu.find(m * n)] - cnt + 1;
    }
};