4.29
- 访问数组某一位后其后面若干位会进入缓存,缓存运行速度较快。因此多维数组可以通过优化循环顺序提高运行速度。
- ::a 可用来访问全局变量。
- 从 \(i\) 到 \(j\) 走 \(k\) 步的方案数可用矩阵加速。\(C=a^k\),a表示邻接矩阵。具体见图:

4.30
- 运用逆元对除法做模运算(适用范围:\(b,p\) 互质)。
若p为质数,运用费马小定理:
\[a^{p-1}\equiv1\pmod{p}\Rightarrow a^{p-2}\equiv\dfrac{1}{a}\pmod{p} \]\[a/b\equiv a/b^{p-2}\pmod{p} \]否则,运用欧拉定理:
\[a/b\equiv a/b^{\varphi(m)-2}\pmod{p} \]- 求 \(\varphi(n)\)。(类似容斥)
喜报:扩展欧几里得算法全面碾了费马小定理,时间复杂度相同,但扩欧不要求互素。
根据逆元定义可得 \(a\cdot x\equiv 1\pmod{p}\),\(x\) 为 \(a\) 的逆元。显然,\(k\cdot p+1\equiv 1\pmod{p}\),由此可得:
\[a\cdot x+k\cdot p=1 \]这就可以用扩欧求解了。
-
求逆元
- \(O(n)\) 阶乘和阶乘逆元预处理,然后可以将 \(n\to 1\) 的逆元全部求出(约分)。
代码:
fac[0]=1;
for(int i=1;i<=n;++i) fac[i]=1ll*fac[i-1]*i%p;
ifac[n]=ksm(fac[n],p-2,p);
for(int i=n-1;i>=0;--i) ifac[i]=1ll*ifac[i+1]*(i+1)%p;
for(int i=1;i<=n;++i) inv[i]=1ll*fac[i-1]*ifac[i]%p;
- 递推。
代码:
inv[1]=1;
for(int i=2;i<=n;++i)
{
int k=p/i,r=p%i;
inv[i]=1ll*(p-k)*inv[r]%p;//p-k同余于-k
}
- Miller-Rabin 素性测试
若 \(n\) 为素数,取 \(a<n\),设 \(n-1=d\cdot2^r\),至少满足如下两条性质中的一条:
\[a^d\equiv1\pmod{n} \]\[\exists 0\leq i <r,a^{d\cdot 2^i}\equiv -1\pmod{n} \]代码:
点击查看代码
bool Miller-Rabin(int n,int a)
{
int d=i-1,r=0;
while(!d%2) d/=2,++r;
int x=ksm(a,d,n);
if(x==1) return 1;
for(int i=0;i<r;++i)
{
if(x==n-1) return 1;
x=1ll*x*x%n;
}
return 0;
}
bool is_prime(int now)//写法1
{
for(int i=1;i<=50;++i)
{
int a=rand()%(n-1)+1;
if(!now%a) return 0;
}
return 1;
}
bool is_prime(int now)//写法2(成功率较高)
{
if(now<2) return 0;
for(int i=1;i<8;++i)
{
if(now==prime_list[i]) return 1;
if(!now%prime_list[i]) return 0;
if(!Miller-Rabin(now,prime_list[i]%n)) return 0;
}
return 1;
}
int exgcd(int a,int b,int &x,int &y)
{
if(!b) { x=1,y=0; return a; }
int g=exgcd(b,a%b,x,y);
int temp=x;
x=y,y=temp-y*a/b;
return g;
}
- 中国剩余定理
显然,两个同余方程可解出一个同余方程。暴力做法是进行枚举,每次加 \(\max(q1,q2)\),直至 \(x>lcm(q1,q2)\)。(但这个暴力不好卡 qaq)
可以发现这样就和扩展欧几里得算法类似,就可以写出如下代码(学长的代码挂掉了,放的是我在模板题解中学习的方法):
点击查看代码
#include<bits/stdc++.h>
#define ll long long
#define ld long double
using namespace std;
ll n,p[100005],a[100005];
ll exgcd(ll a,ll b,ll &x,ll &y)
{
if(!b){ x=1,y=0; return a; }
ll g=exgcd(b,a%b,x,y);
ll temp=x;
x=y,y=temp-a/b*y;
return g;
}
ll mul(ll a,ll b,ll md)
{
ll ans=0;
while(b)
{
if(b&1) ans=(ans+a)%md;
a=(a+a)%md;
b>>=1;
}
return ans;
}
ll EXCRT()
{
ll x,y;
ll ans=a[1],P=p[1];
for(int i=2;i<=n;++i)
{
ll B=p[i],C=(a[i]-ans%B+B)%B;
ll g=exgcd(P,B,x,y),temp=B/g;
if(C%g) return -1;
x=mul(x,C/g,temp)/*a2-a1并不一定是P,B的gcd,因此需要乘(a2-a1)/gcd(P,B)*/,ans+=x*P,P*=temp,ans=(ans%P+P)%P;
}
return (ans%P+P)%P;
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin>>n;
for(int i=1;i<=n;++i) cin>>p[i]>>a[i];
cout<<EXCRT()<<endl;
return 0;
}
- 筛法
- 埃氏筛
直接上代码:
for(int i=2;i<=n;++i)
for(int j=i<<1;j<=n;j+=i)
not_prime[b]=1;
复杂度 \(O(n\log n)\),Vergil证过,但我忘了怎么证了。
稍加优化:
for(int i=2;i<=n;++i)
if(!not_prome[i])
for(int j=i<<1;j<=n;j+=i)
not_prime[j]=1;
复杂度 \(O(n\log\log n)\)。
- 欧拉筛
按照上面的思想,每个数都会被它的许多质因子筛一次,这就会造成一定浪费。
代码:
for(int i=2;i<=n;++i)
{
if(!not_prime[i]) prime[++cnt]=i;
for(int j=1;j<=cnt;++j)
{
int x=prime[j]*i;
if(x>n) break;
not_prime[x]=1;
if(!i%prime[j]) break;//保证只被最小的素数筛
}
}
- 积性函数:对于互素的 \(a,b\),\(f(a)\cdot f(b)=f(ab)\).
完全积性函数:对于任意的 \(a,b\),\(f(a)\cdot f(b)=f(ab)\).
\(\varphi\) 就是积性函数,这很容易证明。
若 \(i,p[j]\) 不互素,则对于 \(\varphi(i)\) 的质因子不做改变,只改变原公式中的 \(n\),即:
\[\varphi(i\cdot p[j])=\varphi(i)\cdot p[j] \]递推求 \(\phi\) 代码:
for(int i=2;i<=n;++i)
{
if(!not_prime[i]) prime[++cnt]=i;
for(int j=1;j<=cnt;++j)
{
int x=prime[j]*i;
if(x>n) break;
not_prime[x]=1,phi[x]=(prime[j]-1)*phi[i];
if(!i%prime[j]) { phi[x]=phi[i]*prime[j]; break; }
}
}
5.1
- 北上广深(BSGS)
给定质数 \(a,b,p\),求 \(x\) 使得 \(a^x\equiv b\pmod{p}\).很明显暴力复杂度 \(O(p)\).
如果将 \(a^i\) 分组,每组 \(s\) 个,如果在第 \(j\) 组出现解,则 \(b\cdot a^{-j\cdot s}\) 一定在第一组出现。
代码:
int solve(int a,int b,int p)
{
int s=sqrt(p);
int v=1;
set<int> se;
for(int i=0;i<s;++i)
{
se.insert(v);
v=1ll*v*a%p;
}
for(int i=0;i*s<=p;++i)
{
int c=1ll*b*ksm(ksm(a,i*s,p),p-2,p)%p;
if(se.count(c))
{
v=ksm(a,i*s,p);
for(int j=i*s;;++j)
{
if(v==b) return j;
v=1ll*v*a%p;
}
}
}
}
复杂度 \(O(\sqrt{n})\),带个 \(\log\)。
- 组合数学
杨辉三角,递推,加法原理,乘法原理都会hh。
- 选任意多,共有 \(2^n\) 种方案。
- 对于 \(n \geq 1\),
证明:
\[\dbinom{n}{1}=\dbinom{n-1}{0}+\dbinom{n-1}{1} \]\[\dbinom{n}{2}=\dbinom{n-1}{1}+\dbinom{n-1}{2} \]\[\dots \]多次枚举,可以发现,这些可以刚好消掉,不严谨地证毕。
PS:因为 \(\dbinom{n}{m}\) 一定为整数,所以可以考虑分子分母约分。
- 二项式定理
真没想到就是这个
\((x+y)^n\) 各项系数等于杨辉三角第 \(n+1\) 行系数。
\[(x+y)^n=\sum_{i=0}^{n}\dbinom{n}{i}x^{n-i}y^{i} \]与递推结合一下,可得展开 \(k\) 次:
\[\dbinom{n}{m}=\sum_{i=0}^{k}\dbinom{k}{i}\cdot\dbinom{n-k}{m-k+i}=\sum_{i=0}^{k}\dbinom{k}{i}\cdot\dbinom{n-k}{m-i} \]由前一个式子到后一个式子可以理解为将连续加和反向,写可以设 \(j=k-i\),得 \(\sum_{j=0}^{k}\dbinom{n-k}{m-j}\),再将 \(j\) 换成 \(i\).
- 卢卡斯定理
适用于组合数取模,模数为质数。将 \(n,m\) 转化为 \(p\) 进制,则:
其实最原始的公式是这样的,利用递归:
\[\dbinom{n}{m}=\dbinom{n\bmod p}{m\bmod p}\cdot \dbinom{n/p}{m/p} \]浅浅证明一下:
首先有一个前置:\((1+x)^p \equiv1+x^p\pmod p\)
根据二项式定理,前式可以写成如下形式:
\[1+\binom{p}{1}x^1+\binom{p}{2}x^2+\binom{p}{3}x^3+\dots+\binom{p}{k}x^k+\dots+x^p \]\[\binom{p}{i}=\dfrac{p!}{i!\cdot (p-i)!} \]对于质数 \(p\),在 \(\pmod p\) 意义下,中间每一项的结果一定为零;但如果是合数,则会与分子进行约分,这就是扩展卢卡斯定理的范围。
至此,该前置式子已证毕。
接下来证明定理。
设 \(n=sp+q,m=tp+r\).
\[\dbinom{n}{m}=\dbinom{q}{r}\cdot \dbinom{s}{t} \]对于 \((1+x)^n=(1+x)^{sp+q}=[(1+x)^p]^s\cdot (1+x)^q\),所求即为 \(x^m\) 项的系数。
上式 \(\equiv(1+x^p)^s\cdot (1+x)^q\).
二项式展开,试图开卷,可以看出前一个式子只能得到幂次大于等于 \(p\) 的项,而后一个式子只能得到幂次小于 \(p\) 的项。\(m=tp+r\),所以前一个式子要提供 \(x^{tp}\),后一个式子要提供 \(x^r\),\(x^m\)项的系数即为该两项的乘积,得出:
证毕。
代码(因为我的不理解,还以为代码又挂了,对不起,贴一下模板):
点击查看代码
#include<bits/stdc++.h>
#define ld long double
#define ll long long
using namespace std;
int t,p,a[100005],b[100005],tail1,tail2,frac[100005];
void first(){ frac[0]=1; for(int i=1;i<=p;++i) frac[i]=1ll*frac[i-1]*i%p; }
int ksm(int x,int mx)
{
int ans=1;
while(mx)
{
if(mx&1) ans=1ll*ans*x%p;
x=1ll*x*x%p;
mx>>=1;
}
return ans;
}
int C(int x,int y)
{
if(y>x) return 0;
return (1ll*frac[x]*ksm(frac[y],p-2)%p*ksm(frac[x-y],p-2)%p);
}
int Lucas(int n,int m)
{
memset(a,0,sizeof(a)),memset(b,0,sizeof(b));
tail1=tail2=0;
while(n) a[++tail1]=n%p,n/=p;
while(m) b[++tail2]=m%p,m/=p;
int ans=1;
for(int i=1;i<=max(tail1,tail2);++i) ans=1ll*ans*C(a[i],b[i])%p;
return ans;
}
int n,m;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin>>t;
while(t--)
{
cin>>n>>m>>p;
first();
cout<<((p==1)?0:Lucas(n+m,n))<<"\n";
}
return 0;
}
exlucas 不咕哩。
首先将 \(p\) 分解质因数,然乎可以拆成多个同余方程:
\[\begin{cases}\dbinom{n}{m}\bmod p_1^{a1}\\\dbinom{n}{m}\bmod p_2^{a2}\\\dots\end{cases} \]之后就可以用 excrt 求解。
很显然,阶乘的逆元不能直接求,因为不一定互质。
那就构造一下,将因子 \(P\) 全部提出。
\[\frac {\frac {n!}{P^{x}}}{\frac {m!}{P^{y}}\frac {(n-m)!}{P^{z}}}P^{x-y-z}\bmod{P^k} \]现在等价于求
\[n!\bmod{P^k} \]其中,\(n!\) 可以写成这种形式:
\[n!\%{p^k}={p^{n/p}}\times (n/p)!\times (\prod\limits_{i,gcd(i,p)=1}^{p^k}i)^{n/p^k}\times(\prod\limits_{i,gcd(i,p)=1}^{p\%k}i)\%p^kn!%p \]即将所有小于 \(n\) 的 \(P\) 的倍数提出,\(P\)的次幂会被消掉,可直接忽略。
显然,剩余部分会构成一个循环节,每 \(P-1\) 个数一个循环,最后会剩余 \(n-\left\lfloor\dfrac{n}{p}\right\rfloor\cdot p\) 个数,前半部分递归,后半部分暴力枚举。
然后就是求其中的 \(x\)。
假设 \(p^{x'}\) 整除 \(\left\lfloor \dfrac{n}{p}\right\rfloor\),\(x=x'+\dfrac{n}{p}\),也递归实现即可。
代码:
点击查看代码
#include<bits/stdc++.h>
#define ld long double
#define ll long long
using namespace std;
ll n,m,p,A[100005],pr[100005],cnt;
ll exgcd(ll a,ll b,ll &x,ll &y) {
if(!b) return x=1,y=0,a;
ll g=exgcd(b,a%b,x,y);
ll temp=x;
x=y,y=temp-a/b*y;
return g;
}
ll inv(ll x,ll pi) {
ll a,b;
exgcd(x,pi,a,b);
return (a+pi)%pi;
}
ll ksm(ll x,ll mx,ll md) {
ll ans=1;
x%=md;
while(mx) {
if(mx&1) ans=ans*x%md;
x=x*x%md;
mx>>=1;
}
return ans;
}
ll mul(ll x,ll mx,ll md) {
ll ans=0;
while(mx) {
if(mx&1) (ans+=x)%=md;
(x+=x)%=md;
mx>>=1;
}
return ans;
}
ll fac(ll x,ll pi,ll tol) {
if(x==0) return 1;
ll cir=1,rem=1;
for(ll i=1;i<=tol;++i) if(i%pi) cir=cir*i%tol;
cir=ksm(cir,x/tol,tol);
for(ll i=tol*(x/tol);i<=x;++i) if(i%pi) rem=rem*(i%tol)%tol;
return fac(x/pi,pi,tol)*cir%tol*rem%tol;
}
ll sum(ll x,ll pi){ return x<pi?0:sum(x/pi,pi)+x/pi; }
ll C(ll pi,ll tol) {
ll k1=fac(n,pi,tol),k2=inv(fac(m,pi,tol),tol),k3=inv(fac(n-m,pi,tol),tol),k4=ksm(pi,sum(n,pi)-sum(m,pi)-sum(n-m,pi),tol);
return k1*k2%tol*k3%tol*k4%tol;
}
ll excrt() {
ll x,y;
ll ans=A[1],P=pr[1];
for(int i=2;i<=cnt;++i) {
ll B=pr[i],C=(A[i]-ans%B+B)%B;
ll g=exgcd(P,B,x,y),temp=B/g;
x=mul(x,C/g,temp),ans+=x*P,P*=temp,ans=(ans%P+P)%P;
}
return (ans%P+P)%P;
}
ll exlucas() {
ll P=p;
for(ll i=2;i*i<=p;++i)
if(!(P%i)) {
ll temp=1;
while(!(P%i)) temp*=i,P/=i;
pr[++cnt]=temp;
A[cnt]=C(i,temp);
}
if(P!=1) pr[++cnt]=P,A[cnt]=C(P,P);
return excrt();
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
cin>>n>>m>>p;
cout<<exlucas()<<"\n";
return 0;
}
如P3746,首先运用二项式定理。
\[\begin{aligned} &\quad\sum_{i=0}^{\infty}\sum_{j=0}^{k}\dbinom{k}{j}\cdot\dbinom{nk-k}{ik+r-j}\\ &=\sum_{j=0}^{k}\sum_{i=0}^{\infty}\dbinom{k}{j}\cdot\dbinom{nk-k}{ik+r-j}\\ & =\sum_{j=0}^{k}\dbinom{k}{j}\cdot f(n-1,r-j)\end{aligned}\]将 \(f\) 增加一维,转化为矩阵的形式。
\[f_n[1][r]=\sum_{j=0}^{k}f_{n-1}[1][r-j]\cdot D[r-j][r] \]\[D[r-j][r]=\dbinom{k}{j} \]- 抽屉原理
模型:将 \(n+1\) 个物品放入 \(n\) 个抽屉中,必定有两个物品放入同一个抽屉。
- 容斥原理
很容易理解的一个东西,公式如下。

5.2
- 可以将较强的要求拆解,转换为较弱的条件,再利用容斥解决。
- 高斯消元
就这篇博客放这儿你敢说不会?
就这题你怎么过的 \(hack\) 数据你敢说不会?
竟然不讲约旦!

- 计算逆矩阵
只有对角线为 \(1\) 的矩阵为单位矩阵。
交换单位矩阵第 \(i\) 行和第 \(j\) 行的 \(1\),等于交换该两行。
改变单位矩阵第 \(i\) 行第 \(j\) 列,即将第 \(j\) 行加到第 \(i\) 行。
将原矩阵与单位矩阵一起进行高斯消元,可求得原矩阵逆矩阵。
放一下模板代码:
点击查看代码
#include<bits/stdc++.h>
#define ll long long
#define ld long double
using namespace std;
const int p=1e9+7;
ll n,a[405][805];
ll ksm(ll x,ll mx)
{
ll ans=1;
while(mx)
{
if(mx&1) ans=ans*x%p;
x=x*x%p;
mx>>=1;
}
return ans%p;
}
void g_j()
{
for(int i=1;i<=n;++i)
{
int temp=i;
for(int j=i+1;j<=n;++j)
if(a[j][i]>a[temp][i])
temp=j;
if(temp!=i)
for(int j=1;j<=(n<<1);++j)
swap(a[i][j],a[temp][j]);
if(!a[i][i]){ cout<<"No Solution"<<endl; return; }
ll w=ksm(a[i][i],p-2);
for(int j=1;j<=n;++j)
if(j!=i)
{
ll r=a[j][i]*w%p;
for(int k=i+1;k<=(n<<1);++k)
a[j][k]=((a[j][k]-a[i][k]*r)%p+p)%p;
}
for(int j=1;j<=(n<<1);++j) a[i][j]=a[i][j]*w%p;
}
for(int i=1;i<=n;++i)
{
for(int j=n+1;j<=(n<<1);++j) cout<<a[i][j]<<' ';
cout<<"\n";
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin>>n;
for(int i=1;i<=n;++i)
{
a[i][i+n]=1;
for(int j=1;j<=n;++j) cin>>a[i][j];
}
g_j();
return 0;
}
你看看你题单里的两紫两黑。
- 求和变形
- 换元法
见下:

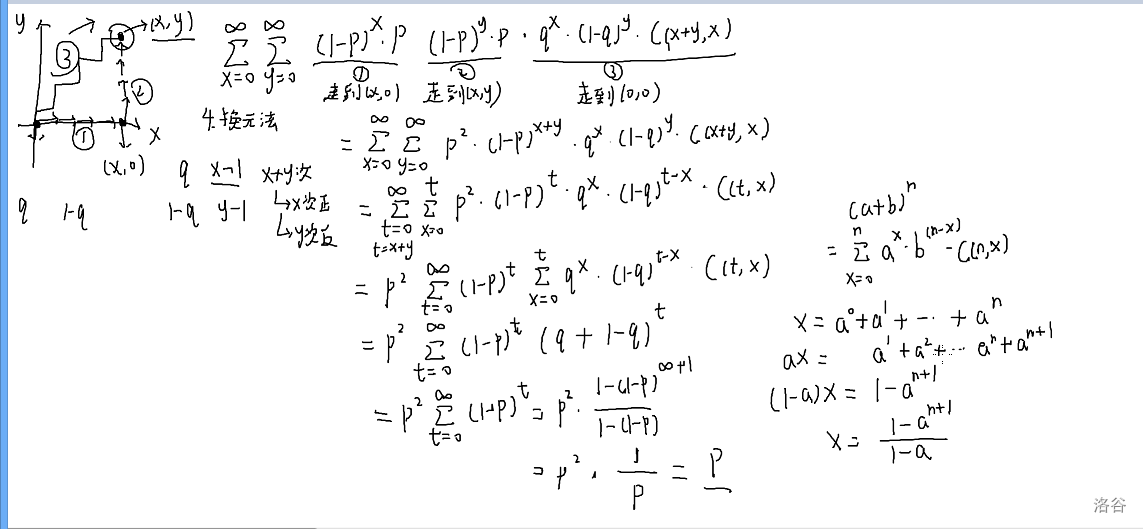
结课啦,芜湖(zhx学长性格好好啊)。
标签:return,dbinom,int,ll,山东,笔记,cdot,ans,集训 From: https://www.cnblogs.com/cat-and-code/p/17478406.html