山东集训笔记

标签：return dbinom int ll 山东笔记 cdot ans 集训

4.29

访问数组某一位后其后面若干位会进入缓存，缓存运行速度较快。因此多维数组可以通过优化循环顺序提高运行速度。
::a 可用来访问全局变量。
从 \(i\) 到 \(j\) 走 \(k\) 步的方案数可用矩阵加速。\(C=a^k\)，a表示邻接矩阵。具体见图：

4.30

运用逆元对除法做模运算（适用范围：\(b,p\) 互质）。

若p为质数，运用费马小定理：

\[a^{p-1}\equiv1\pmod{p}\Rightarrow a^{p-2}\equiv\dfrac{1}{a}\pmod{p} \]

\[a/b\equiv a/b^{p-2}\pmod{p} \]

否则，运用欧拉定理：

\[a/b\equiv a/b^{\varphi(m)-2}\pmod{p} \]

求 \(\varphi(n)\)。（类似容斥）

\[\varphi(n)=n\times\dfrac{p_1-1}{p_1}\times\dots\times\dfrac{p_k-1}{p_k} \]

喜报：扩展欧几里得算法全面碾了费马小定理，时间复杂度相同，但扩欧不要求互素。

根据逆元定义可得 \(a\cdot x\equiv 1\pmod{p}\)，\(x\) 为 \(a\) 的逆元。显然，\(k\cdot p+1\equiv 1\pmod{p}\)，由此可得:

\[a\cdot x+k\cdot p=1 \]

这就可以用扩欧求解了。

求逆元

\(O(n)\) 阶乘和阶乘逆元预处理，然后可以将 \(n\to 1\) 的逆元全部求出（约分）。

代码：

fac[0]=1;
for(int i=1;i<=n;++i) fac[i]=1ll*fac[i-1]*i%p;
ifac[n]=ksm(fac[n],p-2,p);
for(int i=n-1;i>=0;--i) ifac[i]=1ll*ifac[i+1]*(i+1)%p;
for(int i=1;i<=n;++i) inv[i]=1ll*fac[i-1]*ifac[i]%p;

递推。

\[p \bmod i \]

\[p=k\cdot i+r \]

\[-r\equiv k\cdot i\pmod{p} \]

\[\dfrac{1}{i}\equiv \dfrac{k}{-r}\pmod{p} \]

代码：

inv[1]=1;
for(int i=2;i<=n;++i)
{
        int k=p/i,r=p%i;
        inv[i]=1ll*(p-k)*inv[r]%p;//p-k同余于-k
}

Miller-Rabin 素性测试

若 \(n\) 为素数，取 \(a<n\)，设 \(n-1=d\cdot2^r\)，至少满足如下两条性质中的一条：

\[a^d\equiv1\pmod{n} \]

\[\exists 0\leq i <r,a^{d\cdot 2^i}\equiv -1\pmod{n} \]

代码：

bool Miller-Rabin(int n,int a)
{
	int d=i-1,r=0;
	while(!d%2) d/=2,++r;
	int x=ksm(a,d,n);
	if(x==1) return 1;
	for(int i=0;i<r;++i)
	{
		if(x==n-1) return 1;
		x=1ll*x*x%n;
	}
	return 0;
}
bool is_prime(int now)//写法1
{
	for(int i=1;i<=50;++i)
	{
		int a=rand()%(n-1)+1;
		if(!now%a) return 0;
	}
	return 1;
}
bool is_prime(int now)//写法2(成功率较高)
{
	if(now<2) return 0;
	for(int i=1;i<8;++i)
	{
		if(now==prime_list[i]) return 1;
		if(!now%prime_list[i]) return 0;
		if(!Miller-Rabin(now,prime_list[i]%n)) return 0;
	}
	return 1;
}

扩展欧几里得算法：给定 \(a\),\(b\)，\(g=gcd(a,b)\)，求使 \(x\cdot a+y\cdot b=g\) 的 \(x,y\)。

\[gcd(a,b)=gcd(b,a \bmod b)=g \]

\[xa+yb=x'b+y'(a \bmod b) \]

\[xa+yb=x'b+y'(a-b \cdot \lfloor \dfrac{a}{b} \rfloor) \]

\[xa+yb=y'a+(x'-y' \cdot \lfloor \dfrac{a}{b}\rfloor)b \]

\[x=y',y=(x'-y' \cdot \lfloor \dfrac{a}{b}\rfloor) \]

代码：

int exgcd(int a,int b,int &x,int &y)
{
		if(!b) { x=1,y=0; return a; }
		int g=exgcd(b,a%b,x,y);
		int temp=x;
		x=y,y=temp-y*a/b;
		return g;
}

中国剩余定理

显然，两个同余方程可解出一个同余方程。暴力做法是进行枚举，每次加 \(\max(q1,q2)\)，直至 \(x>lcm(q1,q2)\)。~~（但这个暴力不好卡 qaq）~~

\[x\bmod p_1=a_1 \]

\[x\bmod p_2=a_2 \]

\[x=k_1\cdot p_1+a_1=k_2\cdot p_2+a_2 \]

\[k_1\cdot p_1-k_2\cdot p_2=a_2-a_1 \]

可以发现这样就和扩展欧几里得算法类似，就可以写出如下代码（学长的代码挂掉了，放的是我在模板题解中学习的方法）：

#include<bits/stdc++.h>
#define ll long long
#define ld long double
using namespace std;
ll n,p[100005],a[100005];
ll exgcd(ll a,ll b,ll &x,ll &y)
{
	if(!b){ x=1,y=0; return a; }
	ll g=exgcd(b,a%b,x,y);
	ll temp=x;
	x=y,y=temp-a/b*y;
	return g;
}
ll mul(ll a,ll b,ll md)
{
	ll ans=0;
	while(b)
	{
		if(b&1) ans=(ans+a)%md;
		a=(a+a)%md;
		b>>=1;
	}
	return ans;
}
ll EXCRT()
{
	ll x,y;
	ll ans=a[1],P=p[1];
	for(int i=2;i<=n;++i)
	{
		ll B=p[i],C=(a[i]-ans%B+B)%B;
		ll g=exgcd(P,B,x,y),temp=B/g;
		if(C%g) return -1;
		x=mul(x,C/g,temp)/*a2-a1并不一定是P，B的gcd，因此需要乘(a2-a1)/gcd(P,B)*/,ans+=x*P,P*=temp,ans=(ans%P+P)%P;
	}
	return (ans%P+P)%P;
}
int main()
{
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);
	cin>>n;
	for(int i=1;i<=n;++i) cin>>p[i]>>a[i];
	cout<<EXCRT()<<endl;
	return 0;
}

然鹅，这份代码不是严格的中国剩余定理，因为扩展中国剩余定理（不要求互质）也是这份代码。\((?\)

筛法

埃氏筛

直接上代码：

for(int i=2;i<=n;++i)
	for(int j=i<<1;j<=n;j+=i)
		not_prime[b]=1;

复杂度 \(O(n\log n)\)，Vergil证过，但我忘了怎么证了。

稍加优化：

for(int i=2;i<=n;++i)
	if(!not_prome[i])
		for(int j=i<<1;j<=n;j+=i)
			not_prime[j]=1;

复杂度 \(O(n\log\log n)\)。

欧拉筛

按照上面的思想，每个数都会被它的许多质因子筛一次，这就会造成一定浪费。

代码：

for(int i=2;i<=n;++i)
{
	if(!not_prime[i]) prime[++cnt]=i;
	for(int j=1;j<=cnt;++j)
	{
		int x=prime[j]*i;
		if(x>n) break;
		not_prime[x]=1;
		if(!i%prime[j]) break;//保证只被最小的素数筛
	}
}

积性函数：对于互素的 \(a,b\)，\(f(a)\cdot f(b)=f(ab)\).

完全积性函数：对于任意的 \(a,b\)，\(f(a)\cdot f(b)=f(ab)\).

\(\varphi\) 就是积性函数，这很容易证明。

若 \(i,p[j]\) 不互素，则对于 \(\varphi(i)\) 的质因子不做改变，只改变原公式中的 \(n\)，即：

\[\varphi(i\cdot p[j])=\varphi(i)\cdot p[j] \]

递推求 \(\phi\) 代码：

for(int i=2;i<=n;++i)
{
	if(!not_prime[i]) prime[++cnt]=i;
	for(int j=1;j<=cnt;++j)
	{
		int x=prime[j]*i;
		if(x>n) break;
		not_prime[x]=1,phi[x]=(prime[j]-1)*phi[i];
		if(!i%prime[j]) { phi[x]=phi[i]*prime[j]; break; }
	}
}

5.1

北上广深（BSGS）

给定质数 \(a,b,p\)，求 \(x\) 使得 \(a^x\equiv b\pmod{p}\).很明显暴力复杂度 \(O(p)\).

如果将 \(a^i\) 分组，每组 \(s\) 个，如果在第 \(j\) 组出现解，则 \(b\cdot a^{-j\cdot s}\) 一定在第一组出现。

代码：

int solve(int a,int b,int p)
{
	int s=sqrt(p);
	int v=1;
	set<int> se;
	for(int i=0;i<s;++i)
	{
		se.insert(v);
		v=1ll*v*a%p;
	}
	for(int i=0;i*s<=p;++i)
	{
		int c=1ll*b*ksm(ksm(a,i*s,p),p-2,p)%p;
		if(se.count(c))
		{
			v=ksm(a,i*s,p);
			for(int j=i*s;;++j)
			{
				if(v==b) return j;
				v=1ll*v*a%p;
			}
		}
	}
}

复杂度 \(O(\sqrt{n})\)，带个 \(\log\)。

组合数学

杨辉三角，递推，加法原理，乘法原理都会hh。

选任意多，共有 \(2^n\) 种方案。
对于 \(n \geq 1\)，

\[\dbinom{n}{1}-\dbinom{n}{2}+\dbinom{n}{3}-...\dbinom{n}{n}=0 \]

证明：

\[\dbinom{n}{1}=\dbinom{n-1}{0}+\dbinom{n-1}{1} \]

\[\dbinom{n}{2}=\dbinom{n-1}{1}+\dbinom{n-1}{2} \]

\[\dots \]

多次枚举，可以发现，这些可以刚好消掉，~~不严谨地~~证毕。

PS：因为 \(\dbinom{n}{m}\) 一定为整数，所以可以考虑分子分母约分。

二项式定理

~~真没想到就是这个~~

\((x+y)^n\) 各项系数等于杨辉三角第 \(n+1\) 行系数。

\[(x+y)^n=\sum_{i=0}^{n}\dbinom{n}{i}x^{n-i}y^{i} \]

与递推结合一下，可得展开 \(k\) 次：

\[\dbinom{n}{m}=\sum_{i=0}^{k}\dbinom{k}{i}\cdot\dbinom{n-k}{m-k+i}=\sum_{i=0}^{k}\dbinom{k}{i}\cdot\dbinom{n-k}{m-i} \]

由前一个式子到后一个式子可以理解为将连续加和反向，写可以设 \(j=k-i\)，得 \(\sum_{j=0}^{k}\dbinom{n-k}{m-j}\)，再将 \(j\) 换成 \(i\).

卢卡斯定理
适用于组合数取模，模数为质数。将 \(n,m\) 转化为 \(p\) 进制，则：

\[\dbinom{n}{m}=\prod_{i=0}^{mx}\dbinom{a_i}{b_i}\bmod p \]

其实最原始的公式是这样的，利用递归：

\[\dbinom{n}{m}=\dbinom{n\bmod p}{m\bmod p}\cdot \dbinom{n/p}{m/p} \]

浅浅证明一下：

首先有一个前置：\((1+x)^p \equiv1+x^p\pmod p\)

根据二项式定理，前式可以写成如下形式：

\[1+\binom{p}{1}x^1+\binom{p}{2}x^2+\binom{p}{3}x^3+\dots+\binom{p}{k}x^k+\dots+x^p \]

\[\binom{p}{i}=\dfrac{p!}{i!\cdot (p-i)!} \]

对于质数 \(p\)，在 \(\pmod p\) 意义下，中间每一项的结果一定为零；但如果是合数，则会与分子进行约分，这就是扩展卢卡斯定理的范围。

至此，该前置式子已证毕。

接下来证明定理。

设 \(n=sp+q,m=tp+r\).

\[\dbinom{n}{m}=\dbinom{q}{r}\cdot \dbinom{s}{t} \]

对于 \((1+x)^n=(1+x)^{sp+q}=[(1+x)^p]^s\cdot (1+x)^q\)，所求即为 \(x^m\) 项的系数。

上式 \(\equiv(1+x^p)^s\cdot (1+x)^q\).

二项式展开，~~试图开卷~~，可以看出前一个式子只能得到幂次大于等于 \(p\) 的项，而后一个式子只能得到幂次小于 \(p\) 的项。\(m=tp+r\)，所以前一个式子要提供 \(x^{tp}\)，后一个式子要提供 \(x^r\)，\(x^m\)项的系数即为该两项的乘积，得出：

\[\dbinom{n}{m}=\dbinom{s}{t}\cdot\dbinom{q}{r} \]

证毕。

代码（因为我的不理解，还以为代码又挂了，对不起，贴一下模板）：

#include<bits/stdc++.h>
#define ld long double
#define ll long long
using namespace std;
int t,p,a[100005],b[100005],tail1,tail2,frac[100005];
void first(){ frac[0]=1; for(int i=1;i<=p;++i) frac[i]=1ll*frac[i-1]*i%p; }
int ksm(int x,int mx)
{
		int ans=1;
		while(mx)
		{
			if(mx&1) ans=1ll*ans*x%p;
			x=1ll*x*x%p;
			mx>>=1;
		}
		return ans;
}
int C(int x,int y)
{
		if(y>x) return 0;
		return (1ll*frac[x]*ksm(frac[y],p-2)%p*ksm(frac[x-y],p-2)%p);
}
int Lucas(int n,int m)
{
		memset(a,0,sizeof(a)),memset(b,0,sizeof(b));
		tail1=tail2=0;
		while(n) a[++tail1]=n%p,n/=p;
		while(m) b[++tail2]=m%p,m/=p;
		int ans=1;
		for(int i=1;i<=max(tail1,tail2);++i) ans=1ll*ans*C(a[i],b[i])%p;
		return ans;
}
int n,m;
int main()
{
		ios_base::sync_with_stdio(false);
		cin.tie(NULL);
		cout.tie(NULL);
		cin>>t;
		while(t--)
		{
			cin>>n>>m>>p;
			first();
			cout<<((p==1)?0:Lucas(n+m,n))<<"\n";
		}
		return 0;
}

如果 \(p\) 不是质数：需要扩展卢卡斯定理。将 \(p\) 分解质因数，用卢卡斯定理得到多个同余方程，然后利用中国剩余定理合并。

exlucas 不咕哩。

首先将 \(p\) 分解质因数，然乎可以拆成多个同余方程：

\[\begin{cases}\dbinom{n}{m}\bmod p_1^{a1}\\\dbinom{n}{m}\bmod p_2^{a2}\\\dots\end{cases} \]

之后就可以用 excrt 求解。

很显然，阶乘的逆元不能直接求，因为不一定互质。

那就构造一下，将因子 \(P\) 全部提出。

\[\frac {\frac {n!}{P^{x}}}{\frac {m!}{P^{y}}\frac {(n-m)!}{P^{z}}}P^{x-y-z}\bmod{P^k} \]

现在等价于求

\[n!\bmod{P^k} \]

其中，\(n!\) 可以写成这种形式：

\[n!\%{p^k}={p^{n/p}}\times (n/p)!\times (\prod\limits_{i,gcd(i,p)=1}^{p^k}i)^{n/p^k}\times(\prod\limits_{i,gcd(i,p)=1}^{p\%k}i)\%p^kn!%p \]

即将所有小于 \(n\) 的 \(P\) 的倍数提出，\(P\)的次幂会被消掉，可直接忽略。

显然，剩余部分会构成一个循环节，每 \(P-1\) 个数一个循环，最后会剩余 \(n-\left\lfloor\dfrac{n}{p}\right\rfloor\cdot p\) 个数，前半部分递归，后半部分暴力枚举。

然后就是求其中的 \(x\)。

假设 \(p^{x'}\) 整除 \(\left\lfloor \dfrac{n}{p}\right\rfloor\)，\(x=x'+\dfrac{n}{p}\)，也递归实现即可。

代码：

#include<bits/stdc++.h>
#define ld long double
#define ll long long
using namespace std;
ll n,m,p,A[100005],pr[100005],cnt;
ll exgcd(ll a,ll b,ll &x,ll &y) {
	if(!b) return x=1,y=0,a;
	ll g=exgcd(b,a%b,x,y);
	ll temp=x;
	x=y,y=temp-a/b*y;
	return g;
}
ll inv(ll x,ll pi) {
	ll a,b;
	exgcd(x,pi,a,b);
	return (a+pi)%pi;
}
ll ksm(ll x,ll mx,ll md) {
	ll ans=1;
	x%=md;
	while(mx) {
		if(mx&1) ans=ans*x%md;
		x=x*x%md;
		mx>>=1;
	}
	return ans;
}
ll mul(ll x,ll mx,ll md) {
	ll ans=0;
	while(mx) {
		if(mx&1) (ans+=x)%=md;
		(x+=x)%=md;
		mx>>=1;
	}
	return ans;
}
ll fac(ll x,ll pi,ll tol) {
	if(x==0) return 1;
	ll cir=1,rem=1;
	for(ll i=1;i<=tol;++i) if(i%pi) cir=cir*i%tol;
	cir=ksm(cir,x/tol,tol);
	for(ll i=tol*(x/tol);i<=x;++i) if(i%pi) rem=rem*(i%tol)%tol;
	return fac(x/pi,pi,tol)*cir%tol*rem%tol;
}
ll sum(ll x,ll pi){ return x<pi?0:sum(x/pi,pi)+x/pi; }
ll C(ll pi,ll tol) {
	ll k1=fac(n,pi,tol),k2=inv(fac(m,pi,tol),tol),k3=inv(fac(n-m,pi,tol),tol),k4=ksm(pi,sum(n,pi)-sum(m,pi)-sum(n-m,pi),tol);
	return k1*k2%tol*k3%tol*k4%tol;
}
ll excrt() {
	ll x,y;
	ll ans=A[1],P=pr[1];
	for(int i=2;i<=cnt;++i) {
		ll B=pr[i],C=(A[i]-ans%B+B)%B;
		ll g=exgcd(P,B,x,y),temp=B/g;
		x=mul(x,C/g,temp),ans+=x*P,P*=temp,ans=(ans%P+P)%P;
	}
	return (ans%P+P)%P;
}
ll exlucas() {
	ll P=p;
	for(ll i=2;i*i<=p;++i)
		if(!(P%i)) {
			ll temp=1;
			while(!(P%i)) temp*=i,P/=i;
			pr[++cnt]=temp;
			A[cnt]=C(i,temp);
		}
	if(P!=1) pr[++cnt]=P,A[cnt]=C(P,P);
	return excrt();
}
int main() {
	ios_base::sync_with_stdio(false);
	cin.tie(nullptr); cout.tie(nullptr);
	cin>>n>>m>>p;
	cout<<exlucas()<<"\n";
	return 0;
}

有一个很神奇的比较组合数的思路：转换为 \(\log\) 再进行比较。
求和变形

增加枚举量。
交换枚举顺序。
分离无关变量。

如P3746，首先运用二项式定理。

\[\begin{aligned} &\quad\sum_{i=0}^{\infty}\sum_{j=0}^{k}\dbinom{k}{j}\cdot\dbinom{nk-k}{ik+r-j}\\ &=\sum_{j=0}^{k}\sum_{i=0}^{\infty}\dbinom{k}{j}\cdot\dbinom{nk-k}{ik+r-j}\\ & =\sum_{j=0}^{k}\dbinom{k}{j}\cdot f(n-1,r-j)\end{aligned}\]

将 \(f\) 增加一维，转化为矩阵的形式。

\[f_n[1][r]=\sum_{j=0}^{k}f_{n-1}[1][r-j]\cdot D[r-j][r] \]

\[D[r-j][r]=\dbinom{k}{j} \]

抽屉原理

模型：将 \(n+1\) 个物品放入 \(n\) 个抽屉中，必定有两个物品放入同一个抽屉。

容斥原理

很容易理解的一个东西，公式如下。

5.2

可以将较强的要求拆解，转换为较弱的条件，再利用容斥解决。
高斯消元

就这篇博客放这儿你敢说不会？

就这题你怎么过的 \(hack\) 数据你敢说不会？

竟然不讲约旦！

计算逆矩阵

只有对角线为 \(1\) 的矩阵为单位矩阵。

交换单位矩阵第 \(i\) 行和第 \(j\) 行的 \(1\)，等于交换该两行。

改变单位矩阵第 \(i\) 行第 \(j\) 列，即将第 \(j\) 行加到第 \(i\) 行。

将原矩阵与单位矩阵一起进行高斯消元，可求得原矩阵逆矩阵。

放一下模板代码：

#include<bits/stdc++.h>
#define ll long long
#define ld long double
using namespace std;
const int p=1e9+7;
ll n,a[405][805];
ll ksm(ll x,ll mx)
{
	ll ans=1;
	while(mx)
	{
		if(mx&1) ans=ans*x%p;
		x=x*x%p;
		mx>>=1;
	}
	return ans%p;
}
void g_j()
{
    for(int i=1;i<=n;++i)
    {
        int temp=i;
        for(int j=i+1;j<=n;++j)
            if(a[j][i]>a[temp][i])
                temp=j;
        if(temp!=i)
            for(int j=1;j<=(n<<1);++j)
                swap(a[i][j],a[temp][j]);
        if(!a[i][i]){ cout<<"No Solution"<<endl; return; }
        ll w=ksm(a[i][i],p-2);
        for(int j=1;j<=n;++j)
            if(j!=i)
            {
                ll r=a[j][i]*w%p;
                for(int k=i+1;k<=(n<<1);++k)
                    a[j][k]=((a[j][k]-a[i][k]*r)%p+p)%p;
            }
        for(int j=1;j<=(n<<1);++j) a[i][j]=a[i][j]*w%p;
    }
    for(int i=1;i<=n;++i)
    {
        for(int j=n+1;j<=(n<<1);++j) cout<<a[i][j]<<' ';
        cout<<"\n";
    }
}
int main()
{
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);
	cin>>n; 
	for(int i=1;i<=n;++i)
	{
    	a[i][i+n]=1;
	    for(int j=1;j<=n;++j) cin>>a[i][j];
	}
	g_j();
	return 0;
}

概率

\[A\cap B=A\cdot B \]

\[A\cup B=A+B \]

\[A-B=A-A\cdot B \]

\(P(A|B)\) 为条件概率，\(B\) 发生时 \(A\) 发生的概率。

\[P(A|B)=\dfrac{P(AB)}{P(B)} \]

独立事件： \(A,B\) 无关系。

\[P(A)\cdot P(B)=P(AB) \]

即

\[P(A)=P(A|B) \]

期望

你看看你题单里的两紫两黑。

求和变形

换元法

见下：

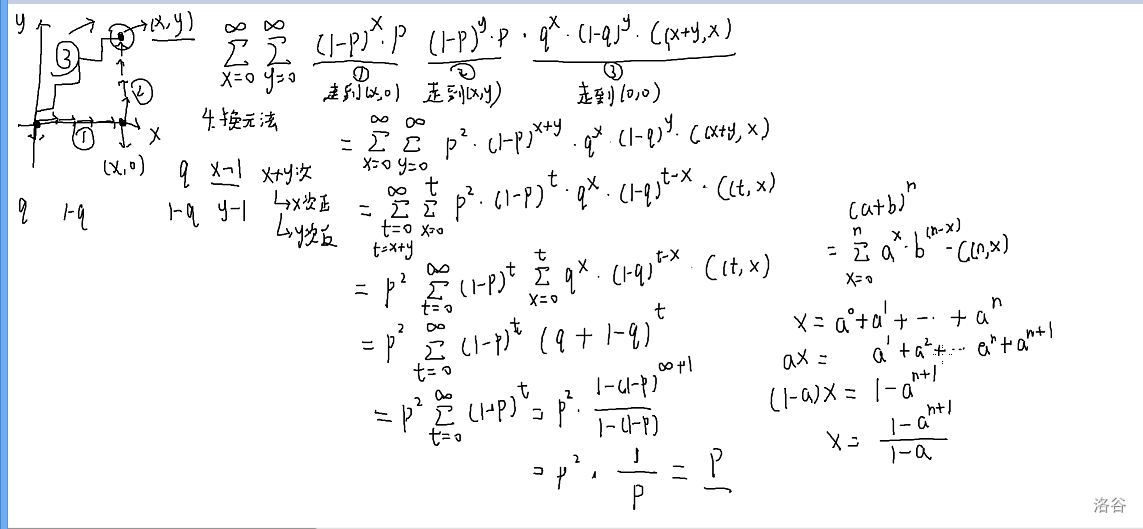
结课啦，芜湖（zhx学长性格好好啊）。

标签：return,dbinom,int,ll,山东,笔记,cdot,ans,集训
From： https://www.cnblogs.com/cat-and-code/p/17474823.html

4.29

4.30

5.1

5.2

相关文章

赞助商

阅读排行