第一部分
什么是动态规划?
"动态规划是一种通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
由于动态规划并不是某种具体的算法,而是一种解决特定问题的方法,因此它会出现在各式各样的数据结构中,与之相关的题目种类也更为繁杂。
在 OI 中,计数等非最优化问题的递推解法也常被不规范地称作 DP,因此本章将它们一并列出。事实上,动态规划与其它类型的递推的确有很多相似之处,学习时可以注意它们之间的异同。" —— oi.wiki
在动态规划的问题中,背包问题是最为经典的一种,在本篇文章里,将以动态规划中最为基础的01背包问题来讲解动态规划的算法核心。
什么是01背包问题?
比如这道例题 洛谷P2871 Charm Bracelet S
题意概要:有 $n$ 个物品和一个容量为 $W$ 的背包,每个物品有重量 $Wi$ 和价值 $Vi$ 两种属性,要求选若干物品放入背包使背包中物品的总价值最大且背包中物品的总重量不超过背包的容量。
在上述例题中,由于每个物体只有两种可能的状态(取与不取),这类问题便被称为「0-1 背包问题」。
换种思路思考01背包问题
假如你在零元购,背着一个只能装下4磅物品的背包,商店里的物品如下
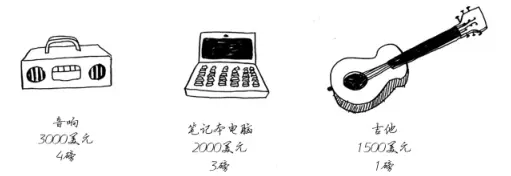
为了让零元购赚的更多,你该如何选择这些商品?
如何解决01背包问题?
最为原始的方法:暴力枚举
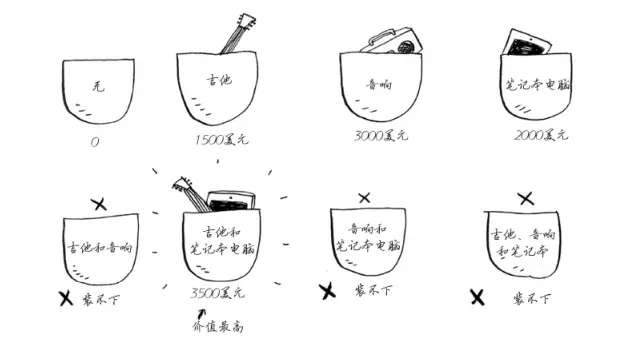
这样是可行的,你可以枚举出8种集合。
但是,我们可以发现,这种方法枚举出的集合数随着商品数量的增加是成指数级增长的。可以得出,这种方法的复杂度是 $O(2$^n$)$ ,显然,这是我们不希望看到的,因为它太慢了。
更进一步:动态规划
每个动态规划都有一张表格
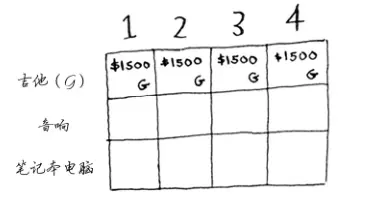
对于01背包问题,我们可以构建一张这样的表格:
-
在表格的第 $i$ 行,能选择 $1→i$ 内的物品
-
怎么理解?如填充表格第一行时,我们只发现了吉他可以零元购,而当填充表格第二行时,我们就发现了吉他和音响可以零元购,以此类推。
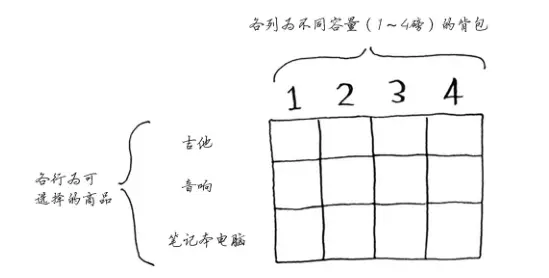
动态规划的核心是:填充其中的每个单元格,网格填满后,你就找到了问题的答案!
为什么会这么说呢?接下来我们来推理一下。
第一步:填充吉他行
动态规划的核心思想是:从子问题开始逐步解决复杂的问题,所以,在这一步,我们需要考虑的仅仅是要不要零元购吉他(如此处不能理解不必纠结,继续跟着思路走完就能理解)
首先,我们来看第一个单元格,在这一行的在每个单元格,我们都需要做一个简单的决定:要不要零元购吉他?
第一个单元格表示背包的的容量为1磅。吉他的重量也是1磅,这意味着它能装入背包!因此这个单元格包含吉他,价值为1500美元。
接下来在表格中填充:
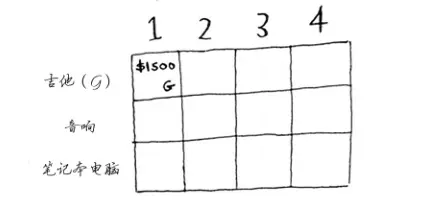
接着,来看下一个单元格。这个单元格表示背包容量为2磅,显然,一样可以装下吉他,以此类推,我们可以填完整第一行。
第二步:填充音响行
我们来填充下一行——音响行。现在处于第二行,你可以零元购的商品有吉他和音响。
和上面一样,我们先来看第一个单元格,在此之前,可装入1磅背包的商品最大价值为1500美元。
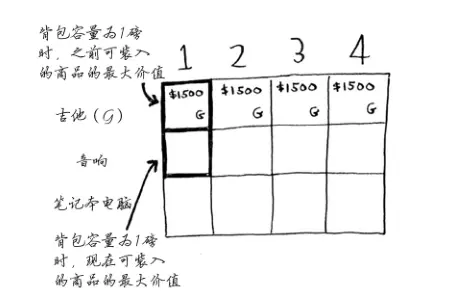
但是,我们发现,背包的容量为1磅,显然不能装下音响,因此1磅容量背包的最大价值依然是1500美元。
接下来的两个单元格的情况与此相同。在这些单元格中,背包的容量分别为2磅和3磅,而以前的最大价值为1500美元。由于这些背包装不下音响,因此最大的价值仍然保持不变。
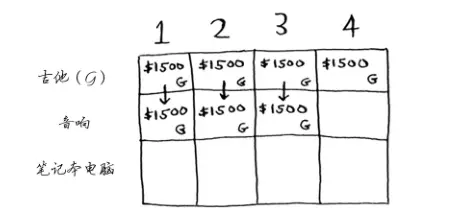
那如果背包容量为4磅呢?终于能够装下音响了!原来最大价值为1500美元,但如果我们在背包中装入音响而不是装入吉他,价值将会变成为3000美元!所以,我们还是换成零元购音响更好。
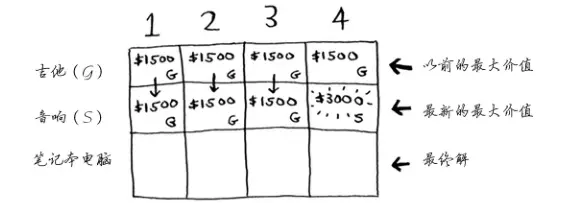
第三步:填充笔记本电脑行
以同样的方式处理笔记本电脑。笔记本电脑重3磅,没法将其装入1磅或者2磅的背包,因此前两个单元格的最大价值仍然是1500美元。
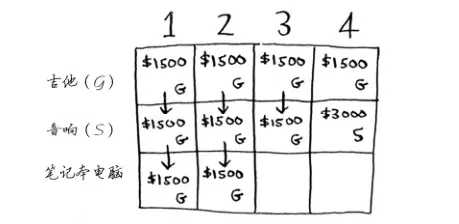
对于容量为3磅的背包,原来的最大价值为1500美元,但现在你可以选择零元购价值2000美元的笔记本电脑而不是零元购吉他,这样新的最大价值将为2000美元。
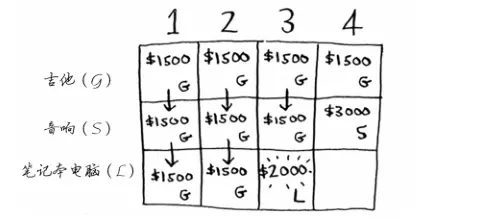
但是,对于容量为4磅的背包,就开始有意思了。这里是整个动态规划中最重要的地方。
在刚才的推导中,我们可以发现,容量为4磅的背包最高可以零元购的价值为3000美元,但是,因为你多了一个笔记本电脑的选择,所以,你可以考虑零元购笔记本电脑而不是刚才零元购的音响。
但是,反应快的同学肯定想到了:但是笔记本电脑没有音响值钱啊!

但事实真的如此吗?
笔记本电脑的重量只有3磅,我们的背包还有1磅的容量没用!

那么,这一磅的重量最大能装的价值为多少呢?
这就是动态规划的核心了:分解复杂问题为子问题来解决问题。
在刚刚的计算中,我们已经计算过1磅背包最大能零元购的价值了。
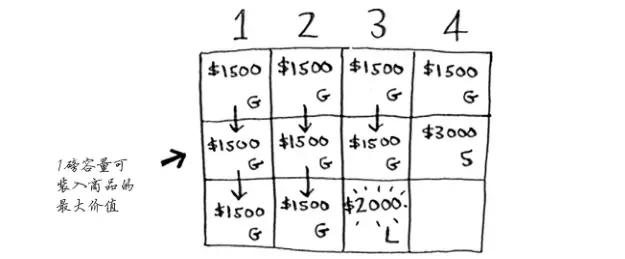
所以,我们将这两个数相加后相加后,最大的价值为:

显然,笔记本电脑和吉他的总价值为3500美元,因此零元购它们是更好的选择。
接着,顺着刚才的思路,我们就能得到如下的伪代码:
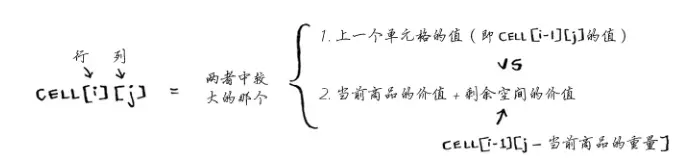
至此,你就学会了动态规划中最基本的01背包。
QA:
Q1:为什么可以这样递推?不用担心重复拿取的问题吗?
A1:从定义上,我们规定了
在表格的第 $i$ 行,能选择 $1→i$ 内的物品
怎么理解?如填充表格第一行时,我们只发现了吉他可以零元购,而当填充表格第二行时,我们就发现了吉他和音响可以零元购,以此类推。
所以不用担心这个问题
再进一步:动态规划滚动数组压维
正在编写中
参考文章
[1] 0-1背包问题(我没有三颗心脏)
[2] OI Wiki
标签:零元,单元格,吉他,01,动态,背包 From: https://www.cnblogs.com/miku10032/p/17470499.html