前言
计算几何的基础基本就是高中学过的内容,一般来说 OI 中应该不会考那些纯数学的解析几何,但是往往会和其它算法结合(比如斜率优化DP,当时学的时候我还不会求凸包,令人感叹)。
前置知识
一些常量

\(\text{Pi}\) :即 \(\pi\) ,用 \(\arccos\) 来求能使精度误差最小。
\(\text{INF}\) 就是一个极大值。
\(\text{eps}\) 往往就是判断两个数是否相等。
浮点数相关
常用函数
\(\text{floor(x)}\) :上取整。
\(\text{ceil(x)}\) :下取整。
\(\text{int(x+0.5)}\) :四舍五入。
浮点误差
由于浮点数的运算不可避免的会有误差,所以,尽量避免三角函数,除法,开方求幂,求对数这一类运算的复合,要不然精度爆炸。
再有就是浮点数判等的两种方法
-
误差判别法:
fabs(x-y) < eps -
完全避免浮点数的使用,手写分数类重载运算符。这玩意工程量就大了,综合考虑我选第一种/cy
向量
高中课本有,这里不做过多赘述。
向量是既有大小又有方向的量,可以用一个带箭头的有向线段表示,线段长度称为模长,线段与平面直角坐标系 \(x\) 轴正方向的夹角称为极角。
同时,向量也可以用实数对,或者叫坐标来表示,记作 \(\overrightarrow{a} = (x,y)\)
代码实现:
struct Point{
double x,y;
}a,b;
向量的运算
加法:\(\overrightarrow{a} + \overrightarrow{b} = (x_1+x_2,y_1+y_2)\)
在代码中,我们往往是重载运算符进行处理。
Point operator +(Point a,Point b)
{
return Point{a.x+b.x,a.y+b.y};
}
引用 wjyyy 的图片
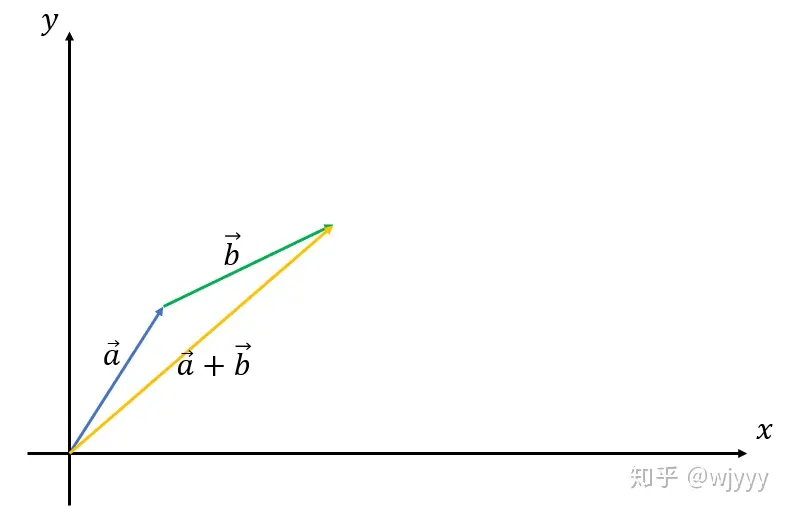
减法:\(\overrightarrow{a} - \overrightarrow{b} = (x_1-x_2,y_1-y_2)\)
Point operator -(Point a,Point b)
{
return Point{a.x-b.x,a.y-b.y};
}
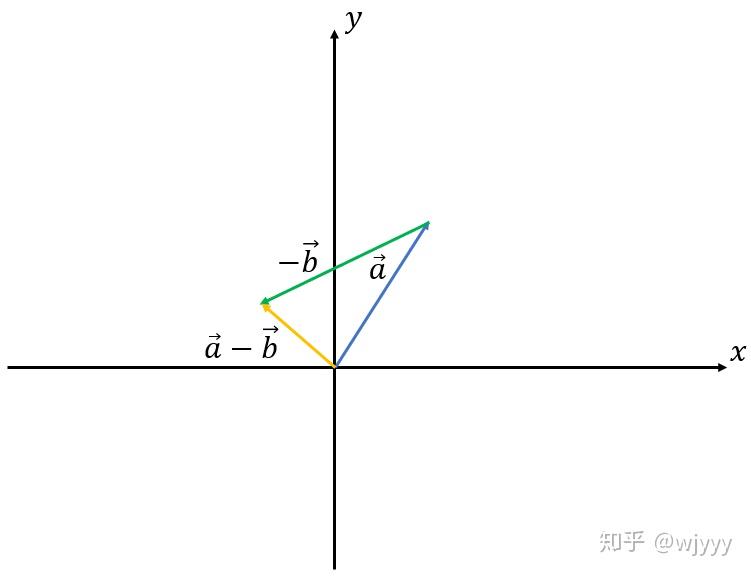
数乘:\(t \overrightarrow{b} = (tx_1,ty_1)\) (\(t\)是常量)
Point operator *(Point a,double t)
{
return Point{t * a.x,t * a.y};
}
点积
-
定义:\(\overrightarrow{a} \cdot \overrightarrow{b} = |\overrightarrow{a}||\overrightarrow{b}|\cos \theta\)
-
几何意义:向量 \(\overrightarrow{b}\) 在 向量 \(\overrightarrow{a}\) 上的投影与 \(\overrightarrow{a}\) 的模长的乘积。
-
坐标运算: \(\overrightarrow{a} \cdot \overrightarrow{b}=x_1x_2 + y_1y_2\)
-
应用:
(1):判断两向量垂直 \(\overrightarrow{a} \cdot \overrightarrow{b} = 0\)
(2):判断两向量平行 \(\overrightarrow{a} \cdot \overrightarrow{b} = |\overrightarrow{a}||\overrightarrow{b}|\)
(3):求两向量的夹角 \(\cos \theta = \frac{\overrightarrow{a} \cdot \overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}\)
double operator &(Point a,Point b) { return a.x*b.x + a.y*b.y; }//点积
double len(Point a) { return sqrt(a&a); }//模长
double Angle(Point a,Point b) { return acos((a&b) / len(a) / len(b)); }//夹角
叉积
-
定义:\(\overrightarrow{a} \times \overrightarrow{b} = |\overrightarrow{a}||\overrightarrow{b}|\sin \theta\)
-
几何意义:向量 \(\overrightarrow{a}\) 与向量 \(\overrightarrow{b}\) 张成的平行四边形的有向面积。\(\overrightarrow{b}\) 在 \(\overrightarrow{a}\) 的逆时针方向为正,顺时针方向为负。
-
坐标运算: \(\overrightarrow{a} \times \overrightarrow{b}=x_1y_2 - y_1x_2\)
-
应用:
(1):判定点线的位置关系
\((\overrightarrow{b}-\overrightarrow{a}) \times (\overrightarrow{c}- \overrightarrow{a}) > 0 \Rightarrow c\) 点在直线 \(ab\) 的左侧
\((\overrightarrow{b}-\overrightarrow{a}) \times (\overrightarrow{c}- \overrightarrow{a}) < 0 \Rightarrow c\) 点在直线 \(ab\) 的右侧
$(\overrightarrow{b}-\overrightarrow{a}) \times (\overrightarrow{c}- \overrightarrow{a}) = 0 \Rightarrow $ 三点共线
il double operator *(Point a,Point b) { return a.x*b.y - a.y*b.x; }//叉积
il double cross(Point a,Point b,Point c) { return (b-a)*(c-a); }//判断c和直线ab的关系
(2):判定线线之间的位置关系
①cross(a,b,c) * cross(a,b,d) > 0\(\Rightarrow\) 直线 \(ab\) 与 线段 \(cd\) 无交点。
②cross(a,b,c) * cross(a,b,d) <= 0\(\Rightarrow\) 直线 \(ab\) 与 线段 \(cd\) 有交点。
\(= 0\) 的情况就是端点 \(c\) 或 \(d\) 在直线 \(ab\) 上。
③线段相交
\(\text{Part 1}\) :判断必不可交的情况
//如果四条判断有一个为真,则代表两线段必不可交,否则应该进行第二步判断。
max(c.x,d.x)<min(a.x,b.x) || max(c.y,d.y)<min(a.y,b.y) || max(a.x,b.x)<min(c.x,d.x) || max(a.y,b.y)<min(c.y,d.y)
\(\text{Part 2}\) : 利用叉积求交
Ⅰ.cross(a,b,c) * cross(a,b,d) > 0 或 cross(c,d,a) * cross(c,d,b) > 0\(\Rightarrow\) 线段 \(ab\) 与 线段 \(cd\) 无交点。
Ⅱ.cross(a,b,c) * cross(a,b,d) <= 0 且 cross(c,d,a) * cross(c,d,b) <= 0\(\Rightarrow\) 线段 \(ab\) 与 线段 \(cd\) 有交点。
注意有交的时候必须两个条件都满足,这样就排除了一个线段在另一个线段的直线上但是不在线段上的情况。
④求两直线的交点
首先一个直线有两种表示方法:两点式(\(\overrightarrow{a},\overrightarrow{b}\)) 或者是点向式 \((\overrightarrow{a},\overrightarrow{b}-\overrightarrow{a})\) 。
两点式就是最常见的两点确定一条直线,点向式则是给定直线上一个点,再求出它沿着这个直线的一段向量。
Point GetNode(Point a,Point u,Point b,Point v)//求交点
{
double t = (a-b)*v / (v*u);
return a + u*t;
}
引用董晓老师的图片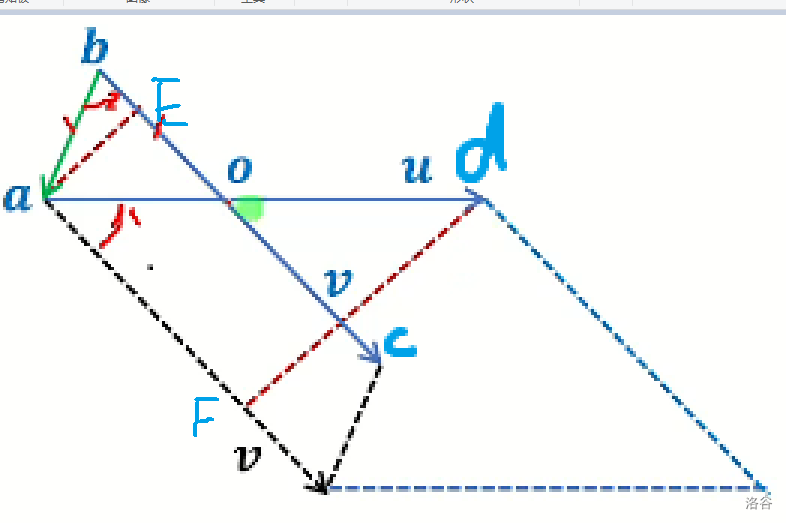
其中 \(a,b\) 是点 , \(\textcolor{black}{u,v}\) 是 \(a,b\) 延伸出来的向量 \(c,d\) 是这两个向量的终点。
先说明 \(t\) 是干什么的, \(t\) 其实就是 \(\overrightarrow{ao}\) 在 \(\overrightarrow{u}\) 上的占比,\(a\) 加上这一段,就能得出交点坐标。
再来看看怎么求出 \(t\) :
首先作出 \(\overrightarrow{a}-\overrightarrow{b}\) ,让它和 \(\overrightarrow{v}\) 作叉积,得到的就是这个黑色平行四边形的面积,并且我们可以知道这个面积是正的。同理,我们把 \(\overrightarrow{v}\) 平移一下, 再让\(\overrightarrow{v}\) 和 \(\overrightarrow{u}\) 作叉积,我们可以得到这个大平行四边形的面积。
我们发现,这两个平行四边形有着一个公共边,作出这两个平行四边形的高线,那么这两个平行四边形的面积之比,就是高线之比。我们又发现
\(\Delta AEO \sim \Delta DFA\) ,所以说这高线之比就是 \(\overrightarrow{ao}\) 在 \(\overrightarrow{u}\) 上的占比。
旋转
设 \(\overrightarrow{a} = (x,y)\) ,倾角为 \(\theta\) ,长度为 \(l = \sqrt{x^2+y^2}\) 。则有 \(x = l\cos \theta , y=l\sin \theta\)。令其逆时针旋转 \(\alpha\) 度角,得到向量 \(\overrightarrow{b} = l\cos(\theta+\alpha),l\sin(\theta + \alpha)\) 。
由三角恒等变化得,
\[\overrightarrow{b} = l(\cos\theta\cos\alpha-\sin\theta\sin\alpha)),l(\sin\theta\cos\alpha+\cos\theta\sin\alpha)) \]\[=(l\cos\theta\cos\alpha-l\sin\theta\sin\alpha,l\sin\theta\cos\alpha+l\cos\theta\sin\alpha) \]把 \(x,y\) 带回来得到
\[\overrightarrow{b} =(x\cos\alpha-y\sin\alpha,y\cos\alpha+x\sin\alpha) \]Point rotate(Point a,double b)
{
return Point{a.x*cos(b)-a.y*sin(b),a.y*cos(b)+a.x*sin(b)};
}//讲a向量顺时针旋转b(弧度制)
三角剖分
三角剖分求多边形面积
如果我们知道了 \(n\) 边形 \(n\) 个顶点的坐标,我们就能利用三角剖分求出面积。先给出公式。
\[S = \frac{1}{2}|\sum_{i=0}^{n-1}P_i \times P_{i+1 \ \text{mod} \ n}| \]感性证明可以看wjyyy的博客。简而言之就是把相邻每两个顶点与原点构成的向量的叉积的数值的一半累加起来,就能得到多边形的面积。可以发现,每个三角形不在多边形内部的部分总能被一个有向面积为负的三角形和有向面积为正的三角形消去。
三角剖分求多边形和圆的相交面积
有点麻烦在的。
步骤
还是类似于求多边形面积的,可以分为三步
-
多边形的每两条相邻的边和圆心构成三角形;
-
算出每个三角形与圆的有向相交面积;
-
根据有向面积的正负累加到答案中。
重点在第二步,分 \(5\) 种情况:
还是董晓老师的图片
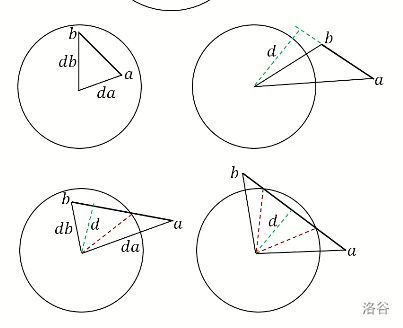
(1): 两个边和圆心共线,面积为 \(0\) ;
(2):两个边都在圆内:是一个三角形的有向面积,对应左上角那个图;
(3):线段完全在圆外:是一个菱形的有向面积,对应右上角那个图;
(4):线段一端在圆内:是一个三角形 \(+\) 一个菱形的有向面积,对应左下角那个图;
(5):线段是圆的割线:是一个三角形 \(+\) 两个菱形的有向面积,注意和第二种情况区分,对应右下角那个图。
代码实现
struct Point{
double x,y;
}o,p[4];
int n;
double R,res = 0;
Point operator +(Point a,Point b) { return Point{a.x+b.x,a.y+b.y}; }//加
Point operator -(Point a,Point b) { return Point{a.x-b.x,a.y-b.y}; }//减
Point operator *(Point a,double t) { return Point{t * a.x,t * a.y}; }//数乘
Point operator /(Point a,double t) { return Point{a.x / t,a.y / t}; }//数除
double operator *(Point a,Point b) { return a.x*b.y - a.y*b.x; }//叉积
double operator &(Point a,Point b) { return a.x*b.x + a.y*b.y; }//点积
double len(Point a) { return sqrt(a&a); }//模长
double dis(Point a,Point b) { return len(b-a); }
double Angle(Point a,Point b) { return acos((a&b) / len(a) / len(b)); }//夹角
double Cross(Point a,Point b,Point c) { return (b-a)*(c-a); }//判断c和直线ab的关系
Point unit(Point a) { return a / len(a); }//单位向量
Point GetNode(Point a,Point u,Point b,Point v)//求交点
{
double t = (a-b)*v / (v*u);
return a + (u*t);
}
Point rotate(Point a,double b) { return Point{a.x*cos(b)-a.y*sin(b),a.y*cos(b)+a.x*sin(b)}; }//讲a向量顺时针旋转b(弧度制)
il bool OnSeg(Point p,Point a,Point b)//判断p是否在线段a,b上
{
return fabs((a-p)*(b-p)) < eps && ((a-p)&(b-p)) <= 0;/*先判断在不在一条直线上,再判断是否在线段上,在线段上点积是负的*/
}
double GetMin(Point a,Point b,Point &pa,Point &pb)//求d以及三角形与圆相交的两个点的坐标
{
Point e = GetNode(a,b-a,o,rotate(b-a,Pi/2));//求线段ab到圆心的垂足
double d = dis(o,e);
if(!OnSeg(e,a,b)) d = min(dis(o,a),dis(o,b));//不在线段ab上,那么最近距离要么是oa,要么是ob
if(R <= d) return d;//线段ab在圆外,没必要求pa和pb了
double Len = sqrt(R*R - dis(o,e)*dis(o,e));//勾股定理求出弦长的一半
pa = e + (unit(a-b) * Len);
pb = e + (unit(b-a) * Len);//向量加法
return d;
}
double Sector(Point a,Point b)//求扇形面积
{
double angle = Angle(a,b);
if(a*b < 0) angle = -angle;//因为angle一定是个正值,想要表示出有向面积就要加个负号
return R*R*angle/2;
}
il double GetArea(Point a,Point b)
{
if(fabs(a*b) < eps) return 0;//共线
double da = dis(o,a) , db = dis(o,b);
if(R >= da && R >= db) return a*b/2;//全在圆内
Point pa,pb;
double d = GetMin(a,b,pa,pb);//d:圆心到线段ab的最近距离
if(R <= d) return Sector(a,b);//全在圆外
if(R >= da) return (a*pb)/2 + Sector(pb,b);//一个点在圆内,一个点在圆外
if(R >= db) return Sector(a,pa) + (pa*b)/2;
return Sector(a,pa) + (pa*pb)/2 + Sector(pb,b);//都在圆外但是是个割线
}
signed main()
{
n = read();
for(re int i=1;i<=n;i++) cin >> p[i].x >> p[i].y;
cin >> o.x >> o.y >> R;
for(re int i=1;i<=n;i++) p[i].x -= o.x , p[i].y -= o.y;
o = Point{0,0};
for(re int i=1;i<=n;i++) res += GetArea(p[i],p[(i+1)%n]);
printf("%.2lf",fabs(res));
return 0;
}
凸包
定义
用通俗的话说,就是平面上有很多点,用一个皮筋刚好圈住所有的点,此时这个皮筋就是这些点的凸包。
凸多边形是指所有内角大小都在 \((0,\pi]\) 范围内的简单多边形。
凸集有一个性质:若 \(a,b\in A\),则 \(c=xa+(1-x)b ,c\in A(0\leq x \leq 1)\),也就是说如果两个点在凸集里,那么它们的连线(线段)上的点也在凸集里。
用数学的话说,就是给定平面上的点集,将最外层的点连接起来构成的凸多边形就叫做凸包。凸包上,点集中的所有点都在凸包上任何一条边所在的直线的同一侧。
具体形状类似于下图。

求解
这里只讲 Andrew 算法(因为我只会这个),用斜率判断也可以(类似斜优 dp),不过精度误差过大。
算法流程
-
对所有点以横坐标为第一关键字,纵坐标为第二关键字进行排序。二者都是小的在前。这样排序完,第 \(1\) 个和第 \(n\) 个点一定是在凸包上的(具体可以看上图)。
-
先顺序枚举所有点,求下凸包。用栈维护当前在凸包上的点,当新点处在栈顶两点构成的有向直线的右侧或共线,就弹出旧点。不能弹出时,新点入栈。
-
再逆序枚举所有点,求上凸包。还是用栈和同样的方法维护一下。
可以看出,每个点入栈,出栈次数不超过 \(2\) 次,所以总次数不会超过 \(4n\) ,最劣的情况就是一条链。
这样,Andrew 算法的复杂度就是 \(O(n\log n)\) 的,瓶颈在于排序的复杂度,求凸包的复杂度是 \(O(n)\) 的。
代码实现
P2742 [USACO5.1]圈奶牛Fencing the Cows /【模板】二维凸包
struct Point{
double x,y;
}p[N];
int n,top;
int s[N<<2];
double ans;
il int read()
{
int f=0,s=0;
char ch=getchar();
for(;!isdigit(ch);ch=getchar()) f |= (ch=='-');
for(; isdigit(ch);ch=getchar()) s = (s<<1) + (s<<3) + (ch^48);
return f ? -s : s;
}
Point operator +(Point a,Point b) { return Point{a.x+b.x,a.y+b.y}; }//加
Point operator -(Point a,Point b) { return Point{a.x-b.x,a.y-b.y}; }//减
il double operator *(Point a,Point b) { return a.x*b.y - a.y*b.x; }//叉积
il double operator &(Point a,Point b) { return a.x*b.x + a.y*b.y; }//点积
il double len(Point a) { return sqrt(a&a); }//模长
il double dis(Point a,Point b) { return len(b-a); }
il double cross(Point a,Point b,Point c) { return (b-a)*(c-a); }//判断c和直线ab的关系
il bool cmp(Point a,Point b) { return a.x == b.x ? a.y < b.y : a.x < b.x; }
signed main()
{
n = read();
for(re int i=1;i<=n;i++) scanf("%lf%lf",&p[i].x,&p[i].y);
sort(p+1,p+n+1,cmp);
for(re int i=1;i<=n;i++)
{
while(top > 1 && cross(p[s[top-1]],p[s[top]],p[i]) <= 0) top--;
s[++top] = i;
}
int t = top;
for(re int i=n-1;i>=1;i--)
{
while(top > t && cross(p[s[top-1]],p[s[top]],p[i]) <= 0) top--;
s[++top] = i;
}
for(re int i=1;i<top;i++) ans += dis(p[s[i]],p[s[i+1]]);
printf("%.2lf",ans);
return 0;
}
旋转卡壳
基础定义
切线:给定一个凸边形 \(P\) ,切线是一条与 \(P\) 相交并且在 \(P\) 一侧的线。可以类比圆的切线来理解。
对踵点对:如果凸多边形的两个点 \(p\) 和 \(q\) 在两条平行切线上,那么它们就构成一对对踵点对。
根据切线与凸多边形的相交方式,可以分以下三种情况:
-
点-点对踵点对,产生 \(1\) 对对踵点对
-
边-点对踵点对,产生 \(2\) 对对踵点对
-
边-边对踵点对,产生 \(4\) 对对踵点对
引用一下董晓老师的图
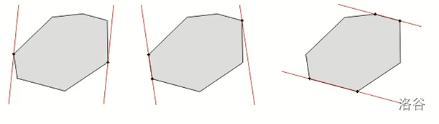
对踵点对的个数是 \(O(n)\) 的,可以证明,一个凸多边形的对踵点对不超过 \(\frac{3n}{2}\) 对。
旋转卡壳:绕着凸多边形旋转一对平行切线,就是旋转卡壳。因为旋转角度可以是任意的,我们不可能挨个角度试,所以,这三种中有意义的就是边-点对踵点对。
应用
有位国外大牛提出了旋转卡壳技术的 \(15\) 个问题,并且给出了具体的实现,国内也有位大牛给出了翻译,这是原文。这些问题包括:
-
计算距离
-
凸多边形直径
-
凸多边形宽
-
凸多边形间最小距离
-
凸多边形间最大距离
-
-
外接矩形
-
最小面积外接矩形
-
最小周长外接矩形
-
-
三角剖分
-
洋葱三角剖分
-
螺旋三角剖分
-
四边形剖分
-
-
凸多边形属性
-
合并凸包
-
找共切线
-
凸多边形交
-
临界切线
-
凸多边形矢量和
-
-
最薄截面
- 最薄横截带
这里只以例题为例,讲几种常用的问题,等以后遇到了别的题再补充。
例题
平面最远点对(凸包直径)
给定 \(n\) 个点,求平面最远点对。
(1)首先,我们证明一下平面最远点对一定是在凸包上的。给个图。
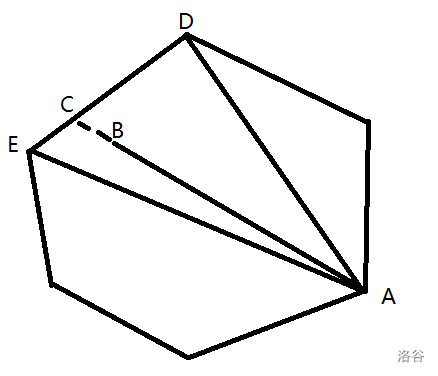
我们假设 \(AB\) 就是最远的。我们延长 \(AB\) ,交 \(DE\) 于点 \(C\) ,连接 \(AD,AE\) 。由于背包的凸性我们一定能找到一个角,要么 \(\angle ACE \ge 90^{\circ}\) ,要么 \(\angle ACE \ge 90^{\circ}\) ,在这个图中就是 \(\angle ACE \ge 90^{\circ}\)。三角形中大边对大角,就有 \(AE > AC\) ,所以说 \(AE > AC > AB\) ,假设不成立。由此,命题得证。
那么问题就转化成立求凸包的直径。凸包的直径是指凸包上最远点对的距离。
(2)接着,我们证明最远点对一定是凸包上的对踵点。

类似于上图的,最远点对一定是一对平行切线和凸包的交点,也就是说最远点对一定是凸包上的对踵点对。如果按逆时针为正方向,凸包上一个点到其他点的距离其实是一个单峰函数,这个可以通过构造三角形看出来,这个峰就是这个点的对踵点。
感性证明完这个结论以后,这个问题就转换成了求凸包上所有对踵点对的距离并取 \(\max\) 即可。凸包直径显然可以暴力 \(O(n^2)\) 求得,运用对踵点对的思想,我们可以优化到 \(O(n)\) 。
(3)再接着,我们再证明一个结论:求对踵点对只用考虑斜率恰好与凸包某条边相同的直线,也就是边-点对踵点对。
我们把点-点对踵点对的两条直线旋转一定角度,一定可以使得其中的一条直线刚好卡住凸包的一条边,形成边-点对踵点对,原先的对踵点对并没有消失,并且我们又形成了新一对对踵点对,由此反复下去,因此,我们只需要考虑边-点对踵点对即可。
(4)最后,我们考虑如何求出对踵点对。
给个图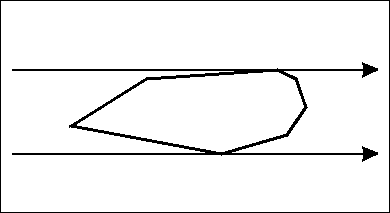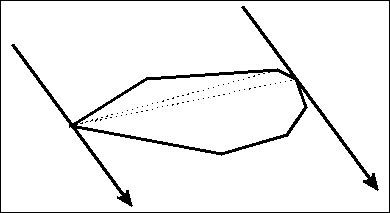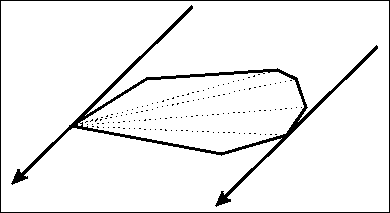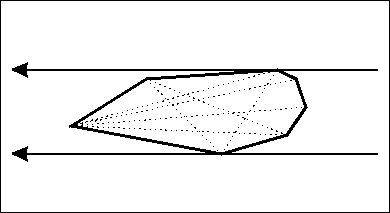
我们可以看出,如果逆时针旋转的话,对踵点对一定是单调逆时针变化的。通过这个结论,我们在找对踵点对的时候,就不用从起点出发一个一个找了。
再一个,我们刚才提到的一个点到其它点的距离是一个单峰函数。具体可以看这张图。

也可以类比刚才的那个(2)中那个平行线,把它从下往上扫,最终扫到一个距离最大的点,这个点就是起点的对踵点。
如果遇上了边-边对踵点对,这时,我们需要特判 \(4\) 对对踵点对。能不能不特判?可以。
引用大佬 \(\text{command\_block}\) 说的话:
我们考虑一个现象 : 假如把所有的点轻微扰动,可以认为卡住对面的两个点这种情况不存在。
而轻微扰动对大多数东西的影响不大,所以我们在大多数题目里面,可以不考虑卡住对面的两个点这种情况。
比如这道题叫我们求的是最远点对,那么可以不特判。
排除了这个因素,我们就可以考虑如何枚举对踵点对了,根据上面那个图我们可以想到一种解法,那就是求三角形的面积,而三角形的面积就可以用叉积来求出,如果下一个三角形的面积大于前一个,指针后移,一直移到一个峰为止。然后下一个对踵点对在从这个峰开始往后找,由于对踵点对的个数是 \(O(n)\) 的,所以找对踵点对的算法的整个复杂度就是 \(O(n)\) 的了。
但是求凸包里面带个 \(\log\) ,所以总复杂度就是 \(O(n\log n)\) 的。
code:
signed main()
{
n = read();
for(re int i=1;i<=n;i++) scanf("%lf%lf",&p[i].x,&p[i].y);
sort(p+1,p+n+1,cmp);
s[++cnt] = p[1];
for(re int i=2;i<=n;i++)
{
while(cnt > 1 && cross(s[cnt-1],s[cnt],p[i]) <= 0) cnt--;
s[++cnt] = p[i];
}
t = cnt;
for(re int i=n-1;i>=1;i--)
{
while(cnt > t && cross(s[cnt-1],s[cnt],p[i]) <= 0) cnt--;
s[++cnt] = p[i];
}
n = cnt - 1;
for(re int i=1,j=2;i<=n;i++)
{
while(cross(s[i],s[i+1],s[j]) < cross(s[i],s[i+1],s[j+1])) j = j % n + 1;
res = max(res,max(dis(s[i],s[j]),dis(s[i+1],s[j])));
}
printf("%d",(int)(res*res));
return 0;
}
凸多边形最大内接四边形
在某块平面土地上有N个点,你可以选择其中的任意四个点,将这片土地围起来,当然,你希望这四个点围成的多边形面积最大。
(1)首先类似的,我们可以得出一个结论:四边形的四个顶点一定在凸包上。如果不在,肯定能多构造出一个三角形使得面积更大。
(2)通过上述结论我们能很轻松的写出一种 \(O(n^4)\) 的算法,但是 \(n\leq2000\),借鉴CSP2022 假期计划的思想,我们给他中间劈开。中间劈开是啥?对角线/cy。我们可以枚举对角线,因为四边形在凸包上,那么对角线也肯定在凸包上。确定了对角线后,再确定另外两个点,由于单峰性和单调性,这两个点我们是可以 \(O(n)\) 求出的。所以求面积的复杂度就是枚举对角线的 \(O(n^2)\) , 总复杂度就是 \(O(n^2 + n\log n)\) ,其实还是 \(O(n^2)\) 。
(3)但其实这个题还没完。如果凸包上只有两个点,说明这 \(n\) 个点在一条直线上,面积为 \(0\) ;如果凸包上有三个点,那么这三个点一定是四边形的三个点,我们 \(O(n)\) 枚举凸包内的点,可以想出这个四边形是个凹四边形,求的时候就用大三角形的面积减去小三角形的面积,取个 \(max\) 就行。
code:
signed main()
{
n = read();
for(re int i=1;i<=n;i++) scanf("%lf%lf",&p[i].x,&p[i].y);
sort(p+1,p+n+1,cmp);
s[++cnt] = p[1];
for(re int i=2;i<=n;i++)
{
while(cnt > 1 && cross(s[cnt-1],s[cnt],p[i]) <= 0) cnt--;
s[++cnt] = p[i];
}
t = cnt;
for(re int i=n-1;i>=1;i--)
{
while(cnt > t && cross(s[cnt-1],s[cnt],p[i]) <= 0) cnt--;
s[++cnt] = p[i];
}
n = cnt - 1;
if(n == 2) return puts("0.000"),0;
if(n == 3)
{
now = INF , res = fabs((s[3]-s[2])*(s[3]-s[1]));
for(re int i=1;i<=n;i++)
{
if((p[i].x == s[1].x && p[i].y == s[1].x) || ((p[i].x == s[2].x && p[i].y == s[2].x)) || ((p[i].x == s[3].x && p[i].y == s[3].x))) continue;
double s1 = fabs((p[i]-s[1])*(p[i]-s[2]));
double s2 = fabs((p[i]-s[2])*(p[i]-s[3]));
double s3 = fabs((p[i]-s[3])*(p[i]-s[1]));
now = min(min(now,s1),min(s2,s3));
}
if(now != INF) res -= now; else res = 0;
printf("%.3lf",res/2.0);
return 0;
}
for(re int i=1;i<=n;i++)
{
int a = i , b = i + 1;
for(re int j=i+1;j<=n;j++)
{
while(cross(s[i],s[a+1],s[j]) > cross(s[i],s[a],s[j])) a = a % n + 1;
while(cross(s[i],s[j],s[b+1]) > cross(s[i],s[j],s[b])) b = b % n + 1;
res = max(res , cross(s[i],s[a],s[j])+cross(s[i],s[j],s[b]));
}
}
printf("%.3lf",res / 2.0);
return 0;
}
面积最小外接矩形
给定一些点的坐标,要求求能够覆盖所有点的最小面积的矩形,输出所求矩形的面积和四个顶点坐标。
依旧先找性质
(1)最小矩形的某条边一定在凸壳的某条边上。
感觉还是比较显然的,如果不在某条边上一定可以再减去一部分矩形。
(2)我们固定一条边,那么它的对边也固定了,就是那个对踵点。接下来考虑矩形的宽怎么确定。
为了保证这个矩形可以框住所有点,那么这个宽一定是最靠左/右的,我们考虑如何找到最靠两边的 \(\rightarrow\) 点积。考虑点积的几何意义,投影长刚好就是它的宽度。由于可以看出这个宽也是具有单峰性质和单调性的,所以可以 \(O(n)\) 求出。所以求最小矩形覆盖的复杂度就是枚举边的 \(O(n)\) 的,总复杂度就是 \(O(n\log n)\) ,瓶颈还是在这凸包上。
附上董晓老师的图片,解释一下一些变量的含义
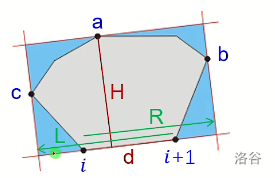
code:
signed main()
{
n = read();
for(re int i=1;i<=n;i++) scanf("%lf%lf",&p[i].x,&p[i].y);
sort(p+1,p+n+1,cmp);
s[++cnt] = p[1];
for(re int i=2;i<=n;i++)
{
while(cnt > 1 && cross(s[cnt-1],s[cnt],p[i]) <= 0) cnt--;
s[++cnt] = p[i];
}
t = cnt;
for(re int i=n-1;i>=1;i--)
{
while(cnt > t && cross(s[cnt-1],s[cnt],p[i]) <= 0) cnt--;
s[++cnt] = p[i];
}
n = cnt - 1 , a = b = 2;
for(re int i=1;i<=n;i++)
{
while(cross(s[i],s[i+1],s[a]) < cross(s[i],s[i+1],s[a+1])) a = a % n + 1;
while(dot(s[i],s[i+1],s[b]) < dot(s[i],s[i+1],s[b+1])) b = b % n + 1;
if(i == 1) c = a;
while(dot(s[i+1],s[i],s[c]) < dot(s[i+1],s[i],s[c+1])) c = c % n + 1;
d = dis(s[i],s[i+1]);
H = cross(s[i],s[i+1],s[a]) / d;
R = dot(s[i],s[i+1],s[b]) / d , L = dot(s[i+1],s[i],s[c]) / d;
if(res > (R+L-d) * H)
{
res = (R+L-d) * H;
ans[1] = s[i+1]+(s[i]-s[i+1]) * (L/d);
ans[2] = s[i]+(s[i+1]-s[i]) * (R/d);
ans[3] = ans[2] + rotate(s[i+1]-s[i],Pi/2) * (H / d);
ans[4] = ans[1] + rotate(s[i+1]-s[i],Pi/2) * (H / d);
}
}
printf("%.5lf\n",res);
int k = 1;
for(re int i=2;i<=4;i++) if(Cmp(ans[i],ans[k])) k = i;
for(re int i=1;i<=4;i++)
{
Zero(k);
printf("%.5lf %.5lf\n",ans[k].x,ans[k].y);
k = k % 4 + 1;
}
return 0;
}
半平面交
一些定义
直线: \(y = kx+b\) 。由初中知识知两点确定一条直线,这里以 \((0,b)\) 和 \((1,k+b)\) 确定一条有向直线,由\((0,b)\) 指向 \((1,k+b)\)。
半平面:直线一侧的平面就叫半平面,左半平面 \(y \geq kx+b\) (包含了这条直线上的点),右半平面 \(y < kx +b\) ,这里其实是向量的运算,\(k\) 不能简单理解成斜率,具体比较麻烦,我们只需要确定一种定向方法并且确定我们要求的是哪一个半平面即可。
半平面交:多个半平面的相交部分,半平面是点集,半平面交肯定也是点集。
半平面交应用:求凸边形的面积交,求线性规划的可行域。
求解-S&I 算法
前置知识
极角排序:C++ 中有一个库函数叫做 atan2(double y,double x),返回的是一个角 \(\theta \in (-\pi,\pi] , \theta = \arctan \frac{y}{x}\) ,这个角其实就是这个直线与 \(x\) 轴的夹角。
算法流程
-
给这些边的方向定为逆时针方向,这样,左平面的交就是半平面交。对这些边按照极角从小到大排序,对于极角相同的两条直线,把靠内的放在前面(靠内的面积肯定是小的)。
-
用双端队列维护边集,逆时针加边。先维护队尾再维护队头。
具体内容见代码,这里以模板题为例:
#include<bits/stdc++.h>
//#define int long long
#define ll long long
#define next nxt
#define re register
#define il inline
const int N = 5e2 + 5;
const double eps = 1e-6;
const double Pi = acos(-1.0);
using namespace std;
struct Point{
double x,y;
}p[N];
struct Line{
Point s,e;
}a[N],q[N];
int n,m,cnt,k;
double res;
il int read()
{
int f=0,s=0;
char ch=getchar();
for(;!isdigit(ch);ch=getchar()) f |= (ch=='-');
for(; isdigit(ch);ch=getchar()) s = (s<<1) + (s<<3) + (ch^48);
return f ? -s : s;
}
Point operator +(Point a,Point b) { return Point{a.x+b.x,a.y+b.y}; }//加
Point operator -(Point a,Point b) { return Point{a.x-b.x,a.y-b.y}; }//减
Point operator *(Point a,double b) { return Point{a.x*b,a.y*b}; }//数乘
il double operator *(Point a,Point b) { return a.x*b.y - a.y*b.x; }//叉积
il double Angle(Line a) { return atan2(a.e.y-a.s.y,a.e.x-a.s.x); }//夹角
Point GetNode(Line a,Line b)//求交点
{
Point u = a.e - a.s , v = b.e - b.s , w = a.s - b.s;
double t = w*v / (v*u);
return a.s + u*t;
}
il bool cross(Line a,Line b,Line c)//判断b和c的交点是否在直线a的右侧
{
Point p = GetNode(b,c);
return (a.e-a.s)*(p-a.s) < 0;
}
il bool cmp(Line a,Line b)
{
double A = Angle(a) , B = Angle(b);
return fabs(A-B) > eps ? A < B : (a.e-a.s)*(b.e-a.s) < 0;
}
il double HalfPlane()
{//共有cnt条边
sort(a+1,a+cnt+1,cmp);
int head = 1 , tail = 1; q[1] = a[1];
for(re int i=2;i<=cnt;i++)
{
if(Angle(a[i]) - Angle(a[i-1]) < eps) continue;
while(head < tail && cross(a[i],q[tail],q[tail-1])) tail--;
while(head < tail && cross(a[i],q[head],q[head+1])) head++;
q[++tail] = a[i];
}
while(head < tail && cross(q[head],q[tail],q[tail-1])) tail--;
q[++tail] = q[head];
for(re int i=head;i<tail;i++) p[++k] = GetNode(q[i],q[i+1]);
for(re int i=1;i<=k;i++) res += p[i]*p[i%k+1];
return res/2;
}
int main()
{
...
}
这里 Line 结构体就是存储的一条边的起点和终点。我们一个函数一个函数解释,那些向量的基础内容就不再说明。
Angle函数
运用 atan2 函数求极角。
GetNode函数
这个其实也算是基础内容,知道了一条直线的两个点,很容易能够转化成点向式。
cmp函数
先是比较极角,把小的放前面,这样就是一个逆时针的顺序了。
如果极角相同,靠左的放在前边,这里的左是有方向的左,注意辨别。
来张图:
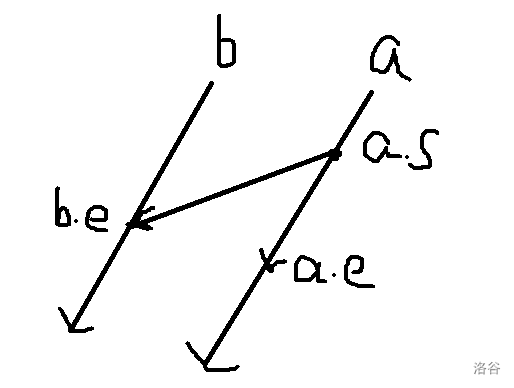
运用叉积的相关性质,如果 (a.e-a.s)*(b.e-a.s) < 0 ,那么就能说明 \(b\) 在 \(a\) 的右侧,我们就可以通过这个来判断位置关系。
cross函数
这个其实和 cmp 函数类似。先用 GetNode 函数求解 \(b\) 和 \(c\) 的交点,再判断这个交点和 \(a\) 的位置关系,原理和上面 cmp 的原理是一样的,将交点类比成 \(b.e\) 即可。
HalfPlane函数
这个其实就是求解的主函数。
首先按极角排序一下,先把第一条直线放进双端队列内,然后开始枚举直线。
开始的第一个 if 就是把极角序相同的排除掉,由于我们已经在排序的时候已经把最靠左的极角序相同的放到前面,所以后面那些靠右的就不用考虑。
接下来就是重头戏,先维护队尾,再维护队头,把交点在当前直线的右边的弹出。
画个图理解一下:
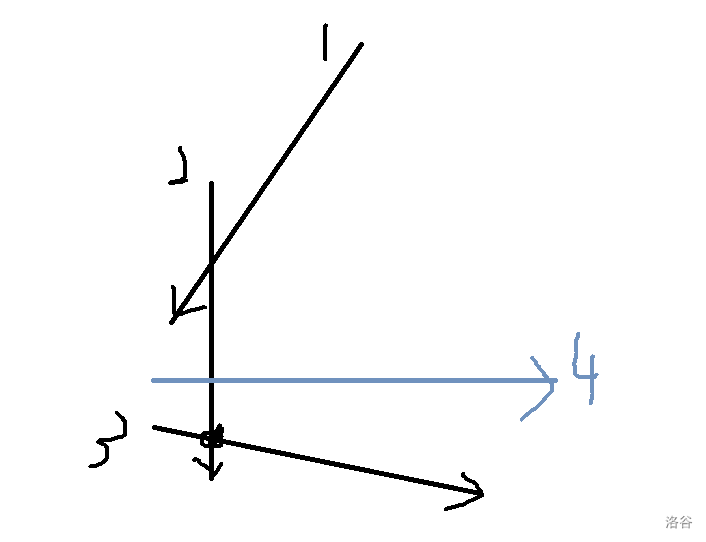
假设我们现在要加入第四条边。我们可以看到,\(2\) 和 \(3\) 的交点在 \(4\) 的右边,这也就说明 \(3\) 和其它直线交的范围要比 \(4\) 和其他直线交的范围多,这也就说明 \(3\) 是需要被弹出的。由于按极角排序了,所以不会出现有些地方是 \(4\) 交到而 \(3\) 没交到的,所以 \(3\) 一定要弹出。对于队头也是同理的。
最后在循环结束的时候还会清空一次队尾,考虑这种情况。

在 \(6\) 加进去以后,我们可以发现都是合法的,但是我们把第一条直线延伸一下就能发现端倪:\(6\) 是多余的,因此在函数最后,我们要去除多余的队尾。而队头是不会多余的,因为在循环里的第二个 while 里已经判断了。
再考虑为什么先队尾后队头,再考虑一种情况:

如果我们先队头后队尾,那么最终只会剩下 \(3,4\) 两条边,围成的面积就是 \(\angle AOD\) 围成的面积;如果先队尾后队头,那么就剩下 \(1,4\) 两条边,围成的面积 \(\angle CBD\) 围成的面积,显然,正确的应该是 \(\angle CBD\) 围成的面积。
由此,我们就能得出全部的对半平面交有用的边了,通过再次调用 GetNode 函数,我们就可以得出边之间的交点,从而能够求出半平面交的面积。
时间复杂度 \(O(n\log n)\) ,复杂度瓶颈还是在于排序。
闵可夫斯基和
入门建议看吉老师(吉如一)的计算几何入门到放弃。感觉应该是讲的最通俗易懂的了。
定义
两个图形(也就是点集) \(A,B\) 的闵可夫斯基和定义为 \(C = \{a+b\mid a\in A,b\in B\}\)。
画一画图可以看出,闵可夫斯基和形成的图形就是一个图形 \(A\) 绕着图形 \(B\) 转一圈。
在 OI 中,我们只考虑凸包的闵可夫斯基和。
性质
一、
两个凸包的闵可夫斯基和还是凸包。
证明:
考虑凸集的一个性质:若 \(a,b\in A\),则 \(c = xa+(1-x)b ,c\in A(0\leq x \leq 1)\)。
设 \(a_1,a_2\in A,b_1,b_2 \in B\) ,根据闵可夫斯基和的定义,\(a_1+b_1,a_2+b_2\in C\)
任取一个
\[x\in[0,1],x(a_1+b_1)+(1-x)(a_2+b_2) \]\[= [xa_1+(1-x)a_2] + [xb_1(1-x)b_2] \]\[[xa_1+(1-x)a_2]\in A, [xb_1(1-x)b_2]\in B \]证毕。
二、闵可夫斯基和上的边是由两个凸包的边构成的
这个不好证,但是可以用我们的瞪眼法看出来应该是对的。给个典图。
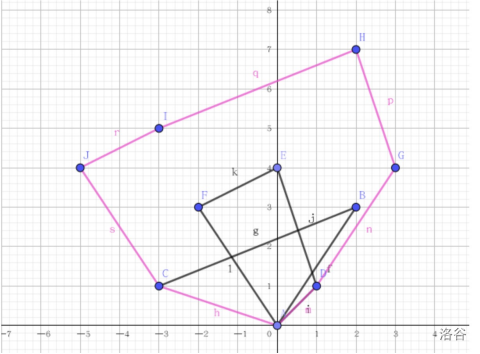
有了这两个性质,我们就能求闵可夫斯基和了。
求法
思路比较简单,但是细节比较多。
因为我们得到 \(A,B\) 两个凸包后,它们的极角序其实是已经排好了的,所以我们就可以采用类似于归并排序的策略,将两个凸包结合起来。
得到闵可夫斯基和后,因为有可能会出现三点共线的情况,所以要再求一次凸包。
il void Minkovski()
{
for(re int i=1;i<n;i++) a[i] = s[i+1] - s[i]; a[n] = s[1] - s[n];//s是A凸包
for(re int i=1;i<m;i++) b[i] = h[i+1] - h[i]; b[m] = h[1] - h[m];//h是B凸包
int p1 = 1 , p2 = 1;
tot = 1 , G[tot] = s[1] + h[1];//归并加入一下,G数组就是闵可夫斯基和
while(p1 <= n && p2 <= m) tot++ , G[tot] = G[tot-1] + (a[p1]*b[p2]>=0 ? a[p1++]:b[p2++]);//极角序从小到大并从G[tot-1]开始往后接
while(p1 <= n) tot++ , G[tot] = G[tot-1] + a[p1++];
while(p2 <= m) tot++ , G[tot] = G[tot-1] + b[p2++];
}
我们用类似 a[i] = s[i+1]-s[i] 的操作得出每条边。我们以 s[1]+h[1] 为一个起点开始往后加,每次加的时候就以 G[tot-1] 为基础往后接上。
应用
刚好就是吉如一出的/qd。
一句话题意。
给定两个凸包 \(A,B\),\(q\) 次询问,每次给出一个向量 \(\overrightarrow{x}\),问 \(B\) 平移向量 \(\overrightarrow{x}\) 后,\(A\) 和 \(B\) 是否还有交集。\(n,m,q \leq 10^5\)。
原题上领地是看三角形内部的区域,实际上就是凸包。而问是否有交集,数学化后就有了下面的式子:
如果有交,那么
\[\exists b + \overrightarrow{x} = a(a\in A,b\in B) \]转化一下,则有
\[\overrightarrow{x} \in \{a-b\mid a\in A,b\in B\} \]我们看到这个很像 \(A,B\) 的闵可夫斯基和的形式,但是它们是相减,怎么办?把 \(B\) 取反,就变成闵可夫斯基和的形式了。
按照上述过程求出闵可夫斯基和后,接下来就剩下最后一个问题,如果判断一个点是否在凸包内,这个也比较好算,以图为例:
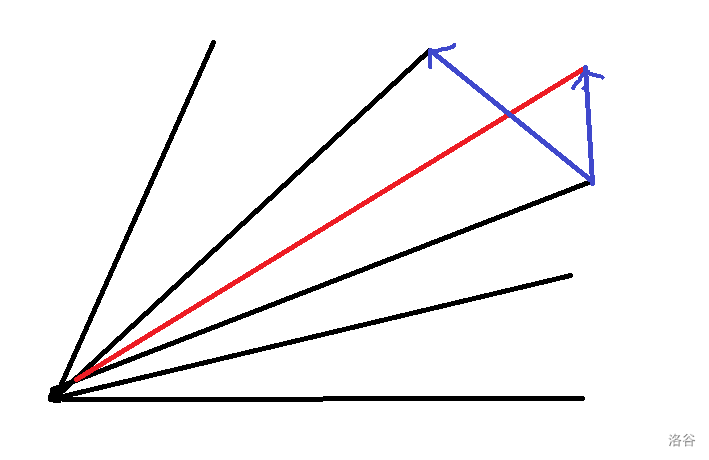
我们选定凸包上最左下角的点为起点,容易得出凸包上其它点的坐标,我们按极角序进行二分,找到当前这个点与起点的连线位于凸包上哪两条线之间。然后如图连两条线,运用叉积运算判断这个点是在凸包外还是在凸包内即可。
另外还有一些小细节,我会在代码中写清。
#include<bits/stdc++.h>
//#define int long long
#define ll long long
#define next nxt
#define re register
#define il inline
const int N = 1e5 + 5;
const double eps = 1e-6;
const double Pi = acos(-1.0);
using namespace std;
struct Point{
double x,y;
}a[N],b[N],s[N],h[N],A[N],G[N],d,st;
int n,m,q,tot;
il int read()
{
int f=0,s=0;
char ch=getchar();
for(;!isdigit(ch);ch=getchar()) f |= (ch=='-');
for(; isdigit(ch);ch=getchar()) s = (s<<1) + (s<<3) + (ch^48);
return f ? -s : s;
}
Point operator +(Point a,Point b) { return Point{a.x+b.x,a.y+b.y}; }//加
Point operator -(Point a,Point b) { return Point{a.x-b.x,a.y-b.y}; }//减
il double operator *(Point a,Point b) { return a.x*b.y - a.y*b.x; }//叉积
il double operator &(Point a,Point b) { return a.x*b.x + a.y*b.y; }//点积
il double cross(Point a,Point b,Point c) { return (b-a)*(c-a); }//判断c和直线ab的关系
il double len(Point a) { return sqrt(a&a); }
il bool cmp(Point a,Point b) { return a.x == b.x ? a.y < b.y : a.x < b.x; }//以x为第一关键字,y为第二关键字排序
il bool cmp2(Point a,Point b) { return a*b > 0 || (a*b == 0 && len(a) < len(b)); }//按极角序排序,如果极角相同短的放前边
il void ConvexHull(Point *s,Point *p,int &n)//s是凸包数组,p是原数组
{
int cnt = 0;
sort(p+1,p+n+1,cmp);
s[++cnt] = p[1];
for(re int i=2;i<=n;i++) //Andrew求凸包
{
while(cnt > 1 && cross(s[cnt-1],s[cnt],p[i]) <= 0) cnt--;
s[++cnt] = p[i];
}
int t = cnt;
for(re int i=n-1;i>=1;i--)
{
while(cnt > t && cross(s[cnt-1],s[cnt],p[i]) <= 0) cnt--;
s[++cnt] = p[i];
}
n = cnt - 1;//第一个点加了两次,别忘了-1
}
il void Minkovski()
{
memset(a , 0 , sizeof a);
memset(b , 0 , sizeof b);//重复利用一下a,b数组,其实可以不memset
for(re int i=1;i<n;i++) a[i] = s[i+1] - s[i]; a[n] = s[1] - s[n];//最后一条线单独写一下
for(re int i=1;i<m;i++) b[i] = h[i+1] - h[i]; b[m] = h[1] - h[m];
int p1 = 1 , p2 = 1;
tot = 1 , G[tot] = s[1] + h[1];//以s[1]+t[1]为起点开始加
while(p1 <= n && p2 <= m) tot++ , G[tot] = G[tot-1] + (a[p1]*b[p2]>=0 ? a[p1++]:b[p2++]);
while(p1 <= n) tot++ , G[tot] = G[tot-1] + a[p1++];
while(p2 <= m) tot++ , G[tot] = G[tot-1] + b[p2++];
}
il bool Judge(Point a)
{
if(a*A[1] > 0 || A[tot]*a > 0) return 0;//绝对不可能在凸包内的情况
int pos = lower_bound(A+1,A+tot+1,a,cmp2) - A - 1;//lower_bound求的是第一个极角序不小于它的,所以减个1
return (a-A[pos])*(A[pos%tot+1]-A[pos])<=0;//如上文所说
}
signed main()
{
n = read() , m = read() , q = read();
for(re int i=1;i<=n;i++) scanf("%lf%lf",&a[i].x,&a[i].y);
for(re int i=1;i<=m;i++) scanf("%lf%lf",&b[i].x,&b[i].y) , b[i].x = -b[i].x , b[i].y = -b[i].y;
ConvexHull(s,a,n);
ConvexHull(h,b,m);
Minkovski();
ConvexHull(A,G,tot);
st = A[1];//选定一个基准点,并且把这个基准点平移到(0,0)的位置上,这样有利于我们求极角序
for(re int i=1;i<=tot;i++) A[i] = A[i] - st;//别的也减一下
while(q--)
{
scanf("%lf%lf",&d.x,&d.y);
printf("%d\n",Judge(d-st));//这个也别忘了减
}
return 0;
}
由此可以看出,整个复杂度是 \(O((n+m+q)\log(n+m))\) 的,\(n,m,q\) 同阶,复杂度也就是 \(O(n\log n)\),可以通过。
平面最近点对
没啥变式,但是分治的思路很妙。
首先,我们按照 \(x\) 为第一关键字,\(y\) 为第二关键字进行排序。
我们现在有 \(n\) 个点,按照 \(x\) 坐标开始分治,把大问题转化为两个子问题。
求出了左右两边的最近点对后,我们更新目前的 \(d\) (即答案)。我们考虑最近点对可能有三种情况:两个都在左边、两个都在右边和一左一右,接下来思考怎么合并。
如果直接暴力枚举,复杂度 \(O(n^2)\) ,肯定不行。这时候利用我们的 \(d\) ,很显然,如果有更优解,两个点一定在 \(mid\) 左右 \(x\) 坐标不超过 \(d\) 的部分,我们只需要枚举这些点。
但是直接枚举仍然有可能是 \(O(n^2)\) 的,这是因为我们只限制了 \(x\) 坐标,没有限制 \(y\) 坐标,导致复杂度错误。
我们把在这 \(2d\) 区域内的点拿出来,按照 \(y\) 坐标排序,然后限制两个点之间 \(y\) 坐标差不超过 \(d\) ,这么做完以后,可以证明,每个点能与它更新的点不超过 \(5\) 个,如图。
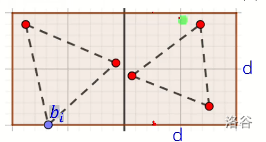
(也有说是 \(9\) 个的,但是反正都是 \(O(1)\) 个)
因为每次要对 \(2d\) 区域内的点排序,所以复杂度是分治 + sort 的 \(O(n\log^2 n)\)。
还可以优化,方法是按照 \(y\) 归并排序,然后合并的时候取出满足 \(x\) 要求的点,这样的复杂度就是 \(O(n\log n)\) 的了。
code:
O(nlog^2n)
il bool cmp1(Point a,Point b) { return a.x == b.x ? a.y < b.y : a.x < b.x; }
il bool cmp2(Point a,Point b) { return a.y < b.y; }
il double solve(int l,int r)
{
if(l == r) return 2e9;
if(l + 1 == r) return dis(a[l],a[r]);
int mid = (l + r) >> 1;
double d = min(solve(l,mid),solve(mid+1,r));
int k = 0;
for(re int i=l;i<=r;i++) if(fabs(a[i].x - a[mid].x) < d) b[++k] = a[i];
sort(b+1,b+k+1,cmp2);
for(re int i=1;i<k;i++)
for(re int j=i+1;j<=k&&b[j].y-b[i].y<d;j++)
d = min(d,dis(b[i],b[j]));
return d;
}
signed main()
{
n = read();
for(re int i=1;i<=n;i++) scanf("%lf%lf",&a[i].x,&a[i].y);
sort(a+1,a+n+1,cmp1);
printf("%.4lf",solve(1,n));
return 0;
}
O(nlogn)
il bool cmp(Point a,Point b) { return a.x == b.x ? a.y < b.y : a.x < b.x; }
il double solve(int l,int r)
{
double d = 2e9;
if(l == r) return d;
int mid = (l + r) >> 1; Point tmp = a[mid];
d = min(solve(l,mid),solve(mid+1,r));
int i = l , j = mid + 1 , k = 0 , t = 0;
while(i <= mid && j <= r)
if(a[i].y < a[j].y) b[++k] = a[i++]; else b[++k] = a[j++];
while(i <= mid) b[++k] = a[i++];
while(j <= r) b[++k] = a[j++];
for(re int i=l,j=1;i<=r;) a[i++] = b[j++];
for(re int i=1;i<=k;i++)
if(fabs(tmp.x-b[i].x) < d) b[++t] = b[i];
for(i=1;i<t;i++)
for(j=i+1;j<=t&&b[j].y-b[i].y<d;j++)
d = min(d,dis(b[i],b[j]));
return d;
}
signed main()
{
n = read();
for(re int i=1;i<=n;i++) scanf("%lf%lf",&a[i].x,&a[i].y);
sort(a+1,a+n+1,cmp);
printf("%.4lf",solve(1,n));
return 0;
}
随机增量法
引入
引用 OI-Wiki 中的话
随机增量算法是计算几何的一个重要算法,它对理论知识要求不高,算法时间复杂度低,应用范围广大。
增量法 (Incremental Algorithm) 的思想与第一数学归纳法类似,它的本质是将一个问题化为规模刚好小一层的子问题。解决子问题后加入当前的对象。写成递归式是:
\(T(n)=T(n-1)+g(n)\)
增量法形式简洁,可以应用于许多的几何题目中。它往往结合随机化,可以避免最坏情况的出现
最小圆覆盖问题
题意
给出 \(N\) 个点,画一个最小的包含所有点的圆。
过程
首先有一个定理:
如果点 \(p\) 不在集合 \(S\) 的最小覆盖圆内,那么 \(p\) 一定在 \(S \cup \{p\}\) 的最小覆盖圆上。
假设圆 \(O\) 是前 \(i-1\) 个点的最小覆盖圆,加入第 \(i\) 个点,如果第 \(i\) 个点在圆内或者圆上,那么什么也不用做;否则,新得到的最小覆盖圆一定经过第 \(i\) 个点。
接下来以第 \(i\) 个点为基础(半径为 \(0\) ) ,重复以上过程依次加入第 $j(j <i) $ 个点,如果第 \(j\) 个点在圆外,那么最小覆盖圆一定经过第 \(j\) 个点。
我们重复以上步骤(因为三点确定一个圆,所以重复三次,是一个三重循环)。
如此遍历完所有点,所得到的圆就是最小覆盖圆。
在算法开始前,我们需要 random_shuffle 一下,以避免最坏情况的出现。
code:
struct Point{
double x,y;
}p[N];
struct Circle{
Point p; double r;
}C;
struct Line{
Point s,t;
}u,v;
Point GetNode(Point a,Point u,Point b,Point v)//求交点
{
double t = (a-b)*v / (v*u);
return a + u*t;
}
Point rotate(Point a,double b) { return Point{a.x*cos(b)-a.y*sin(b),a.y*cos(b)+a.x*sin(b)}; }
Line Midperp(Point a,Point b) { return Line{(a+b)/2,rotate(b-a,Pi/2)}; }//找中垂线
Circle cover(Point a,Point b) { return Circle{(a+b)/2,dis(a,b)/2}; }//覆盖两个点的最小圆就在他俩中点上
Circle cover(Point a,Point b,Point c)//三个点的圆,找中垂线的交点,即为答案
{
u = Midperp(a,b) , v = Midperp(a,c);
Point p = GetNode(u.s,u.t,v.s,v.t);
return Circle{p,dis(p,a)};
}
il void Random_Increment()
{
C = {p[1] , 0};
for(re int i=2;i<=n;i++)
{
if(C.r < dis(C.p,p[i]))
{
C = {p[i] , 0};//一点圆
for(re int j=1;j<i;j++)
{
if(C.r < dis(C.p,p[j]))//两点圆
{
C = cover(p[i],p[j]);
for(re int k=1;k<j;k++)
{
if(C.r < dis(C.p,p[k]))
C = cover(p[i],p[j],p[k]);
}
}
}
}
}
}
signed main()
{
n = read();
for(re int i=1;i<=n;i++) scanf("%lf%lf",&p[i].x,&p[i].y);
random_shuffle(p+1,p+n+1);//随机打乱,保证复杂度
Random_Increment();
printf("%.10lf\n%.10lf %.10lf",C.r,C.p.x,C.p.y);
return 0;
}
这三重循环,看起来像 \(O(n^3)\) 啊,\(10^5\) 的数据怎么过?
但其实,它是 \(O(n)\) 的,考虑证明一下。(证明来自totorato)
由于一堆点最多只有 \(3\) 个点确定了最小覆盖圆,因此 \(n\) 个点中每个点参与确定最小覆盖圆的概率不大于 \(\frac{3}{n}\)
所以,每一层循环在第 \(i\) 个点处调用下一层的概率不大于 \(\frac{3}{i}\)
设算法三个循环的复杂度分别为 \(T_1(n),T_2(n),T_3(n)\) , 则有:
\[T_1(n) = O(n) + \sum_{i=1}^n \frac{3}{i}T_2(i) \]\[T_2(n) = O(n) + \sum_{i=1}^n \frac{3}{i}T_3(i) \]\[T_3(n) = O(n) \]容易看出,\(\sum\frac{3}{i}\) 是个调和级数,近似是个常数,所以 \(T_1(n) = T_2(n) = T_3(n) = O(n)\)