笛卡尔树

下文的资料多摘自OI Wiki

性质

笛卡尔树是一种二叉树，每一个节点都由一个键值二元组 \((k,w)\) 构成。要求 \(k\) 满足二叉搜索树的性质，而 \(w\) 满足堆的性质。如果笛卡尔树的 \(k\) ，\(w\) 键值确定的话，且 \(k\) 互不相同，\(w\) 互不相同，那么这个笛卡尔树的结构是唯一的。

例如：

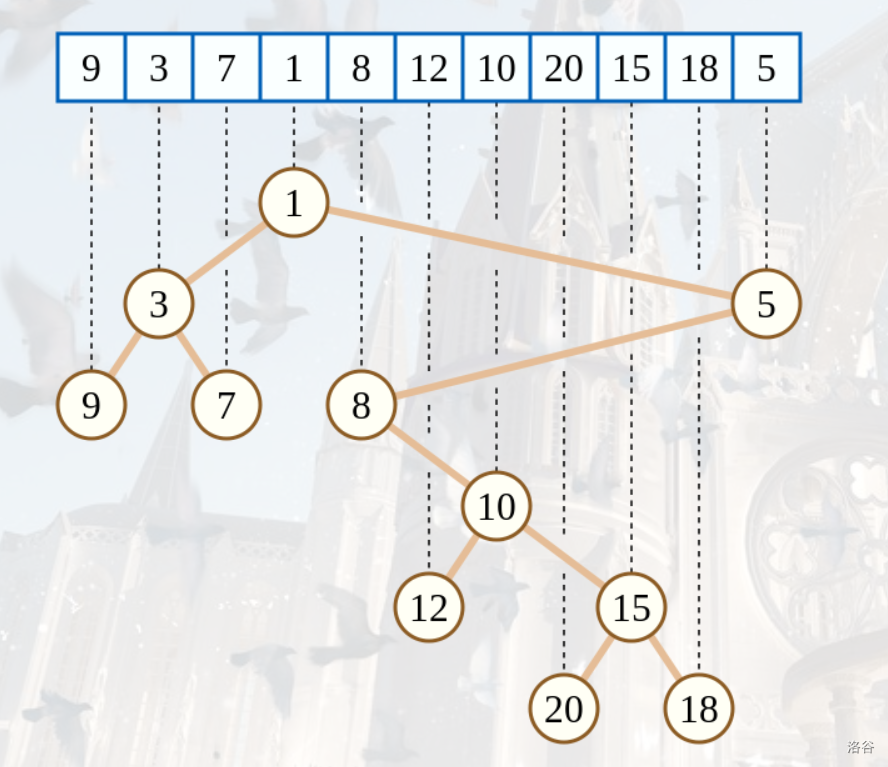
上面的这棵树是按每一个点内的值为键值 \(w\)，把数组下标当作键值 \(k\)，来建立的。仔细观察可以发现，这棵树的 \(k\) 满足二叉搜索树的性质，而键值 \(w\) 是满足小根堆的性质的。

我们由此可以看出,笛卡尔树就是一种键值不随机的 Treap。

构建

过程

我们考虑将元素的键值 \(k\) 进行排序，然后一个一个地插入到当前的笛卡尔树中，那么我们每一次插入的元素必在这个树的右链（右链：从根节点一直往右子树走，经过的节点）的末端。于是我们可以执行这样一个过程，从下往上比较右链节点与当前节点的 \(u\)，和\(w\)，如果找到了一个右链上的节点满足 \(x_{w}<u_{w}\)，就把 \(u\) 接到 \(x\) 的有儿子上，而 \(x\) 原来的右子树就变成了 \(u\) 的左子树。

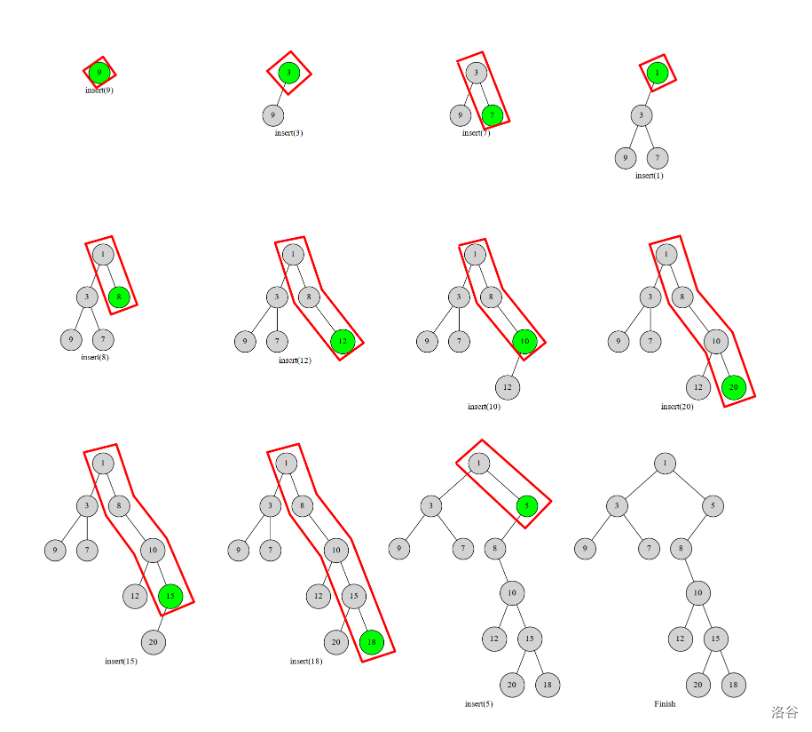
显然每个数最多进出右链一次。这个过程我们可以用栈维护，栈中维护当前笛卡尔树的右链上的结点。这样每个点最多进出一次，复杂度 \(O(n)\)。

更简易的去理解：我们用栈去维护右链，使得 \(k\) 满足二叉搜索树，而为了满足小根堆的状态，我们如果遇到了下面 \(w\) 小上面 \(w\) 大的情况，就不断的进行平衡树中类似的左旋操作，把 \(w\) 小的旋上去，使它满足小根堆的性质。

实现

stk[++top] = 1;
for(re int i=2;i<=n;i++) 
{
	while(top && a[stk[top]] > a[i]) top--;
	if(!top) ls[i] = stk[1];
	else ls[i] = rs[stk[top]] , rs[stk[top]] = i;
	stk[++top] = i;
}

P5854 【模板】笛卡尔树

#include<bits/stdc++.h>
//#define int long long
#define ll long long
#define next nxt
#define re register
#define il inline
const int N = 1e7 + 5;
using namespace std;
int max(int x,int y){return x > y ? x : y;}
int min(int x,int y){return x < y ? x : y;}

int a[N],stk[N],ls[N],rs[N];
int n,top;
ll ans1,ans2;

il int read()
{
	int f=0,s=0;
	char ch=getchar();
	for(;!isdigit(ch);ch=getchar()) f |= (ch=='-');
	for(; isdigit(ch);ch=getchar()) s = (s<<1) + (s<<3) + (ch^48);
	return f ? -s : s;
}

signed main()
{
	n = read();
	for(re int i=1;i<=n;i++) a[i] = read();
	stk[++top] = 1;
	for(re int i=2;i<=n;i++) 
	{
		while(top && a[stk[top]] > a[i]) top--;
		if(!top) ls[i] = stk[1];
		else ls[i] = rs[stk[top]] , rs[stk[top]] = i;
		stk[++top] = i;
	}
	for(re int i=1;i<=n;i++)
	{
		ans1 ^= (1ll * i * (ls[i]+1));
		ans2 ^= (1ll * i * (rs[i]+1));
	}
	cout << ans1 << " " << ans2;
	return 0;
}

笛卡尔树一般就是快速解决区间 \(RMQ\) 问题，但是它是个很鸡肋的存在，大多数情况下用不上这个数据结构。