直方图是由在公共基线处对齐的一系列矩形组成的多边形。
矩形具有相等的宽度,但可以具有不同的高度。
例如,图例左侧显示了由高度为 2,1,4,5,1,3,3
的矩形组成的直方图,矩形的宽度都为 1:
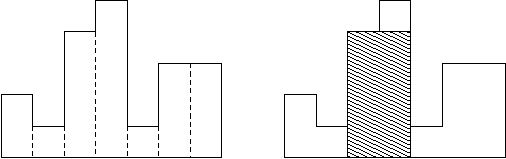
通常,直方图用于表示离散分布,例如,文本中字符的频率。
现在,请你计算在公共基线处对齐的直方图中最大矩形的面积。
图例右图显示了所描绘直方图的最大对齐矩形。
输入格式
输入包含几个测试用例。
每个测试用例占据一行,用以描述一个直方图,并以整数 n
开始,表示组成直方图的矩形数目。
然后跟随 n
个整数 h1,…,hn。
这些数字以从左到右的顺序表示直方图的各个矩形的高度。
每个矩形的宽度为 1
。
同行数字用空格隔开。
当输入用例为 n=0
时,结束输入,且该用例不用考虑。
输出格式
对于每一个测试用例,输出一个整数,代表指定直方图中最大矩形的区域面积。
每个数据占一行。
请注意,此矩形必须在公共基线处对齐。
数据范围
1≤n≤100000
,0≤hi≤1000000000
输入样例:
7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0
输出样例:
8
4000
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, a[N], l[N], r[N];
int stk[N], t = -1; // 用数组模拟堆栈,显然最多有n个数字可能进占
void inStk(int x)
{
stk[++t] = x;
}
bool empStk()
{
if(t >= 0) return false;
return true;
}
int topStk()
{
return stk[t];
}
void popStk()
{
t -- ;
}
void solve();
int main()
{
while(~scanf("%d", &n) && n) // 读入数据,当n == 0时,结束循环
{
for(int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
solve();
}
return 0;
}
void solve()
{
long long ans = 0; // 根据数据范围可知,ans有可能爆int
for(int i = 0; i < n; i ++ ) // 首先找到每个数字的左边离其最近且小于其的数字的位置,使用单调栈的方法
{
while(!empStk() && a[topStk()] >= a[i]) popStk(); // 当栈非空且栈顶元素大于等于当前元素时,不满足条件,将其摄取
if(!empStk()) l[i] = topStk();// 当栈非空时,栈顶元素即为所求位置
else l[i] = -1;// 当栈空时表明没有满足条件的位置
inStk(i);// 将当前数加入栈中
}
while(!empStk()) popStk();// 由于栈中可能有残留,要立即清空,以便再次利用
for(int i = n - 1; i >= 0; i -- )//同理找到右边离其最近且小于其的数字位置
{
while(!empStk() && a[topStk()] >= a[i]) popStk();
if(!empStk()) r[i] = topStk();
else r[i] = n;
inStk(i);
ans = max((long long)(r[i] - l[i] - 1) * (long long)a[i], ans); // 此时左右均找到,求出最大值即可
}
while(!empStk()) popStk();// 由于栈为全局变量,要在使用后清空
printf("%lld\n", ans);
}