题意
给定一个大小为 \(n\times n\) 的字符矩阵,每个字符为 X 或者 O。
对于一个位于 \((x,y)\) 的字符 o 和一个格子 \((u,v)\),如果满足以下条件,那么 \((u,v)\) 就可以被 \((x,y)\) 控制。
- \(x \leqslant u \leqslant n\),\(y \leqslant v \leqslant n\)。
- \((u-x)+\frac{v-y}{2} < m\)。
给定 \(m\) 和询问数 \(Q\),每次询问给定 \(u\) 和 \(v\),求有多少个格子可以控制 \((u,v)\)。
思路
分为两种做法。
0x00
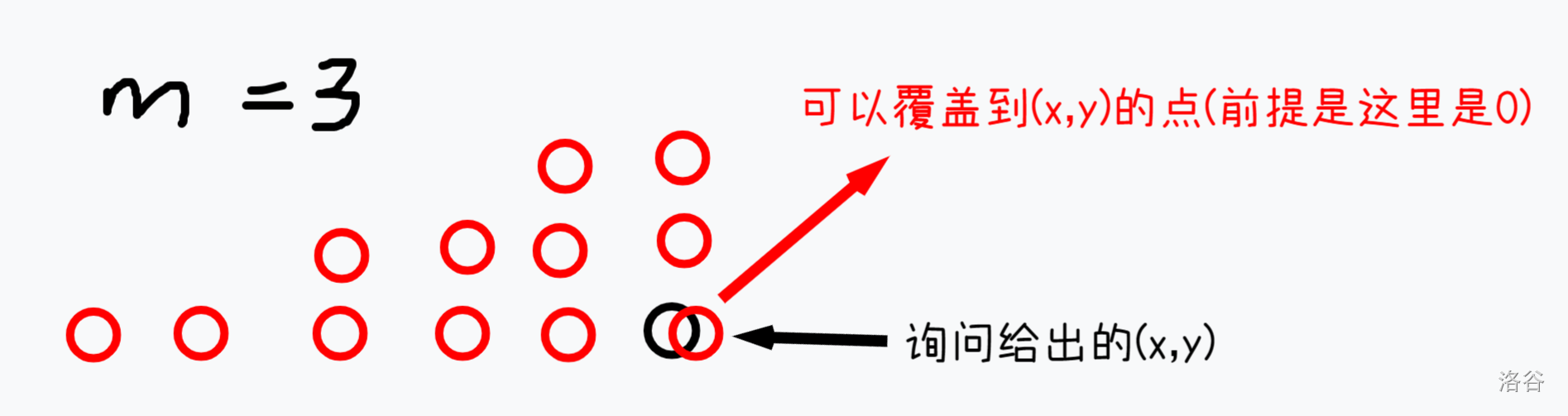
推一推式子,可以发现:
- 第 \(x\) 行第 \((y - 2 \times m) \sim y\) 列的
O都可以控制 \((x,y)\)。 - 第 \(x - 1\) 行第 \((y - 2 \times (m - 1)) \sim y\) 列的
O都可以控制 \((x,y)\)。 - 以此类推。
- 第 \(x - m + 1\) 行第 \(y - 1\) 列与第 \(y\) 列的
O可以控制 \((x,y)\)。 - 第 \(1 \sim (x - m)\) 行没有可以控制 \((x,y)\) 的格子。
做法就出来了,对于每次询问在线求答案即可。
还有一个小问题,枚举每一行和每一列求答案是 \(O(n^2)\) 的,但每一行对答案有贡献的部分是一个区间,可以用前缀和优化,总时间复杂度为 \(O(n^2+ Q\times n)\),并不是最优解法,但可以过此题。
#include <iostream>
using namespace std;
int n, m, q, x, y, sum[2010][2010];
char c;
int main () {
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
cin >> c;
sum[i][j] = sum[i][j - 1] + (c == 'O'); // n 行的前缀和
}
}
for (cin >> q; q; q--) {
cin >> x >> y;
int cnt = 0;
for (int i = 0; i < m && x - i; i++) { // 枚举每一行,如果超出矩阵范围就退出循环
cnt += sum[x - i][y] - sum[x - i][max(0, y - 2 * (m - i))]; // 前缀和
}
cout << cnt << '\n';
}
return 0;
}
0x01
二维差分。

对于一个位于 \((x,y)\) 的 O,可以控制的范围如上,其他的自己推一下(
先对于每一行列差分一下,变成下图:
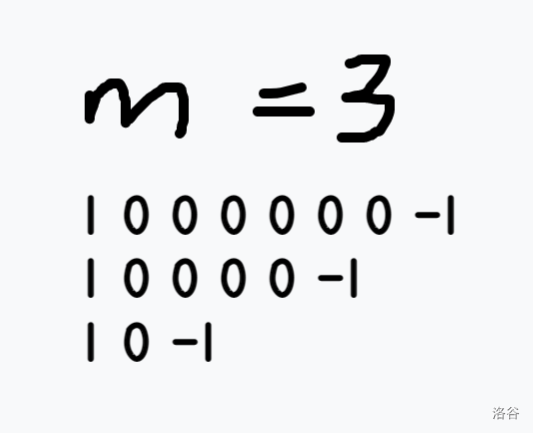
观察上图,可以发现:第一列可以轻松的用行差分优化,但后面的 \(-1\) 怎么办呢?
我们要引入一个差分思想:一个不行就两个!
把这个差分矩阵拆成两个,在最后还原时将两个矩阵加起来。

左边矩阵差分点只有两个,可以 \(O(1)\) 处理差分,可右边怎么办呢?
仔细观察一下,欸,\(-1\) 的位置有规律!
将右边矩阵优化成下图:

差分矩阵通过前缀和思想还原原矩阵,上图每次只要加上 \((x - 1,y + 2)\) 的值就可以了,还原原矩阵时需要将两个差分矩阵加起来,再对它进行列前缀和即可,时间复杂度 \(O(n^2+Q)\)。
具体实现看代码。
#include <iostream>
using namespace std;
int n, m, q, x, y, sum[2010][2010], num[2010][12010][2]; // 注意数组的大小
char c;
int main () {
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
cin >> c;
if (c == 'O') {
num[i][j][0]++, num[min(n + 1, i + m)][j][0]--; // 左边矩阵
num[i][j + 2 * m][1]--, num[min(n + 1, i + m)][j][1]++; // 右边矩阵
}
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n + 2 * m; j++) {
num[i][j][1] += num[i - 1][j + 2][1]; // 左右矩阵各自进行还原
num[i][j][0] += num[i - 1][j][0];
if (j <= n) {
sum[i][j] = sum[i][j - 1] + num[i][j][1] + num[i][j][0]; // 最终的矩阵还原
}
}
}
for (cin >> q; q; q--) {
cin >> x >> y;
cout << sum[x][y] << '\n';
}
return 0;
}