标签：标记 int 线段 DFS 关于 区间 数据结构 节点

1 月 15 日，TSOI2022 迎来了曾获 NOI 铜牌的 Vergil 学长！而 Vergil 线下课的第一个板块就是——数据结构。

本文会梳理 Vergil 所讲的所有数据结构，我们进入正题。

• 2023.2.14 感谢大佬 L3067545513 帮忙修改 LCA~

• 2023.2.19 ST 表被批评了QAQ

线段树

引入

线段树，顾名思义，我们将一个线段看作一个节点，由这样的无数个节点形成的树，我们称之为 线段树。线段树是常见的 维护区间信息 的数据结构。

直接给图：

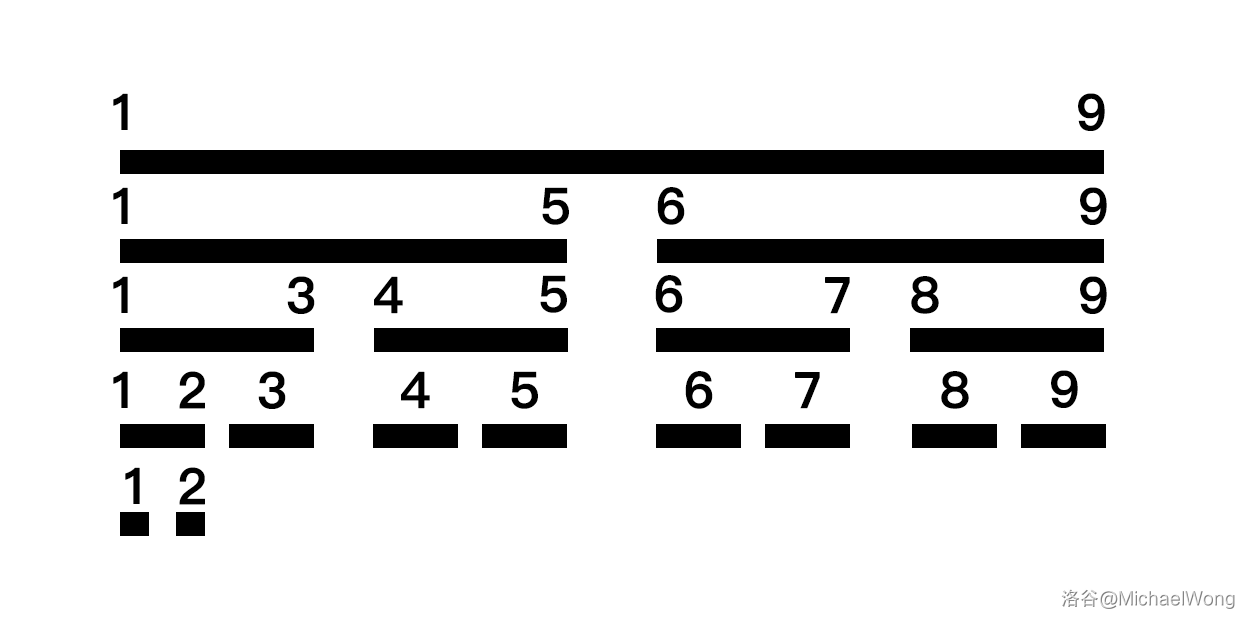
要维护区间 \([1,9]\)，生成的线段树就如上图所示。一般来讲，对于元素数量为 \(x\) 的区间，生成的线段树的节点数量 不会 超过 \(4x\) ，所以开数组时开到 4 倍即可。

我们直接结合 模板题：P3372 【模板】线段树 1 进行讲解。在这道题中，我们需要实现两种操作：

• 区间加：给定 \(l\),\(r\),\(k\)，将 \([l,r]\) 中的所有元素加上 \(k\)。
• 区间查询：给定 \(l\),\(r\),\(k\)，查询 \([l,r]\) 中所有元素的和。

接下来，我们开写。

建树

线段树是一棵 二叉树。所以按照 BFS 序编号时，节点 \(x\) 的两个子节点分别为 \(2x\) 和 \(2x+1\)（即二进制下的 x>>1 和 x>>1|1），我们可以利用这个性质向下遍历。

我们采用 DFS 的方法建树，预处理每个节点所代表的区间 \([L_x,R_x]\) 和该区间内的所有元素的和 \(sum_x\)。

代码如下：

void build(int x,int l,int r)//传参：节点编号，区间边界
{
	L[x]=l;
	R[x]=r;
	if(l==r)
	{
		sum[x]=a[l];
		return;
	}
	int mid=(l+r)>>1;
	build(2*x,l,mid);
	build(2*x+1,mid+1,r);
	sum[x]=sum[2*x]+sum[2*x+1];
	return;
}

区间修改

要修改给定的区间 \([l,r]\) 内的所有元素，如果对所要求的区间 \([l,r]\) 中的所有节点都进行修改，时间复杂度无法承受。所以，在线段树中，我们引入了一个新的变量，巧妙的节约了时间，我们通常称这个变量为 懒标记，代码中常写作 lazy。

顾名思义，懒标记是一个非常 “ 懒 ” 的方法——我们用懒标记记录该节点所代表的区间里每一个元素改变的值，在修改一个区间时，我们只修改表示这个区间的节点，并为它打上懒标记，而不向下修改它的孩子们，这样极大地节省了时间。至于它的孩子们，当需要访问他们的时候，我们再将懒标记 下传。

有了懒标记，我们只需把要修改的区间拆成尽量少的多个区间，使得在线段树中存在若干个节点直接代表拆开后的区间，并对这些区间进行修改即可。

举个栗子，还是 \([1,9]\)，我们建好树后大概就是这个样子：

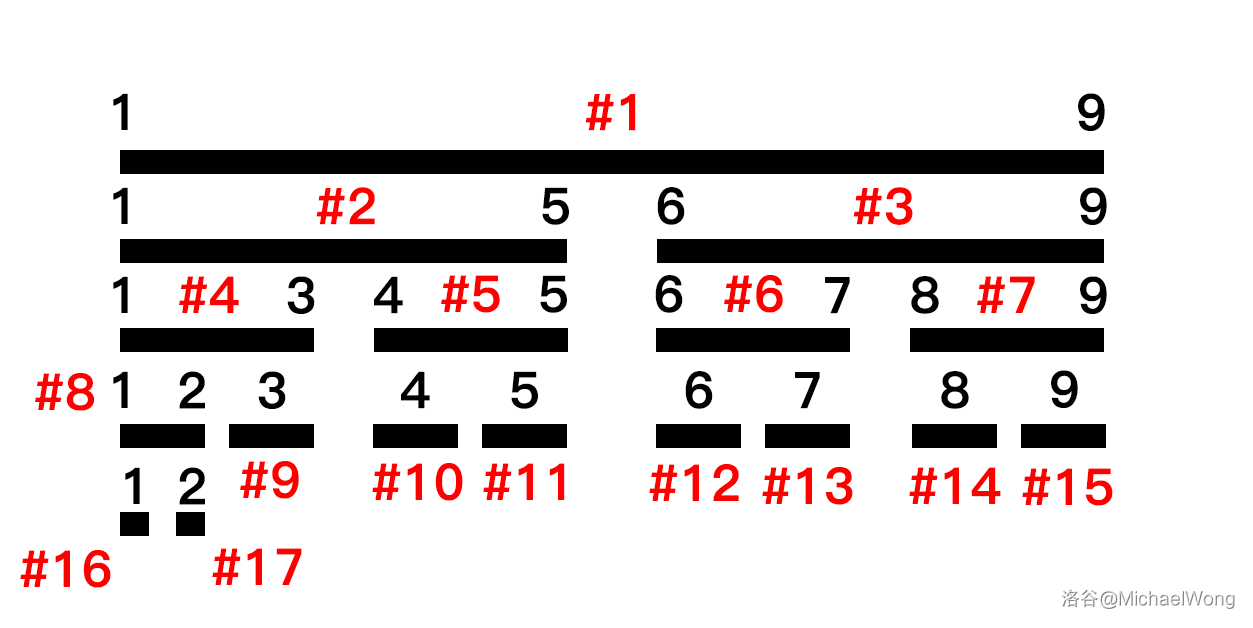
这里我们可以列举几种情况：

• 如果我们要修改 \([1,9]\) ，就直接修改 \(sum_1\) 和 \(lazy_1\)；
• 如果是修改 \([1,3]\)， 就可以通过二分找到 \(\#1 \to \#2 \to \#4\)，然后修改 \(sum_4\) 和 \(lazy_4\)；
• 如果修改 \([5,8]\)，则需要拆成多个区间，节点分别为 \(\#11\)、\(\#6\)、\(\#14\) ，最后修改他们的 \(sum\) 和 \(lazy\)。

特别注意，当我们访问具有懒标记的节点的子节点时，要现将懒标记 下传 ，否则会影响结果。

代码如下：

void change(int x,int l,int r,int z)//当前所在节点，需要修改的区间和修改的值z
{
	if(L[x]==l && R[x]==r)//当前区间就是要修改的区间
	{
		sum[x]+=(R[x]-L[x]+1)*z;//更新sum
		lazy[x]+=z;//更新懒标记
		return;
	}
	int mid=(tree[x].l+tree[x].r)>>1;//当前节点不是要修改的区间，向下二分查找正确区间
	if(tree[x].lazy)	update(x);//访问直接子节点之前，别忘了下传懒标记
	if(r<=mid)	change(2*x,l,r,z);
	else if(l>mid)	change(2*x+1,l,r,z);
	else
	{
		change(2*x,l,mid,z);
		change(2*x+1,mid+1,r,z);
	}
	sum[x]=sum[2*x]+sum[2*x+1];
	return;
}

懒标下传

刚才我们已经介绍了懒标记，简单来说，懒标记帮我们把多次操作记录下来，在向下 访问的时候一起下传修改。所以，懒标下传至关重要。

因为非常简单，我就直接上代码了：

void update(int x)//将x节点的懒标记下传
{
	sum[2*x]+=(R[2*x]-L[2*x]+1)*lazy[x];
	sum[2*x+1]+=(R[2*x+1]-L[2*x+1]+1)*lazy[x];
	lazy[2*x]+=lazy[x];
	lazy[2*x+1]+=lazy[x];
	lazy[x]=0;
}

下传时，只下传一层即可，下传多层同样会浪费时间。

区间查询

与区间修改相同，对于给定的区间 \([l,r]\)，我们把它拆成尽量少的多个区间，使得在线段树中存在若干个节点直接代表拆开后的区间，并对这些区间进行查询，最后输出这些区间查询值的和。

在查询时，如果访问了具有懒标记的节点的子节点，也要记得下传。

代码如下：

long long query(int x,int l,int r)//太大了，必须开朗朗
{
	int mid=(L[x]+R[x])>>1;
	if(L[x]==l && R[x]==r)
		return sum[x];
	if(lazy[x])	update(x);
	if(r<=mid)	return query(2*x,l,r);
	else if(l>mid)	return query(2*x+1,l,r);
	else
		return query(2*x,l,mid)+query(2*x+1,mid+1,r);
}

进阶

上面的内容已经足以通过 模板题：P3372 【模板】线段树 1 了，我们继续结合 模板题：P3373 【模板】线段树 2 讲解一下进阶的操作

在这道题中，我们需要一种新的操作：区间乘。

区间加和区间乘

有聪明的同学可能要说了：我们也像加法一样，为乘法准备一个 独立的懒标记和下传函数 不就可以了吗？

但是，这两个懒标记之间毫无关系吗？显然不是的。

经过简单的推论，我们可以得出：

• 进行区间乘时，该节点的加法和乘法懒标记 也要同时 进行乘法。
• 两个懒标记必须 同时下传。
• 在下传时，子节点的加法和乘法懒标记 都要进行乘法。
• 传递的顺序应该是 先乘后加。

所以，在同时存在多个修改操作时，必须注意各个懒标记之间的联系。

还要注意，乘法懒标记的初始值应为 1。

\(AC\) \(CODE\) here

线段树是一种数据结构，除上文提到的之外还有很多用法，大家可以灵活运用。

---

分块

分块和线段树并非毫无相似之处，值得一提的是，分块 是一种 思想，实质上是一种是通过分成多块后在每块上打标记以实现快速区间修改，区间查询的一种算法，而非 数据结构。

具体来说，线段树是向下二分查找修改区间，而分块更加暴力一些。对于一次区间操作，对区间內部的 整块 进行整体的操作（比如 打懒标记），对区间边缘的零散块单独 暴力处理。所以分块被称为“ 优雅的暴力 ”。

其实，上面的两道线段树例题用分块也是能过的，大家可以去试一下。

分块的块数一般为 \(\sqrt{n}\) 个。 所以说分块的时间复杂度大约为 \(O(\sqrt n)\)，是一种 根号算法，可能比线段树这类 对数级 的要慢一些。但是时间差距不大，而且比线段树好写好想，所以焦头烂额的时候就试试分块吧。

这里推荐一道题：P1503 鬼子进村

具体实现嘛……很简单，分块、打懒标，这里就不赘述了，就说说维护需要的变量：

• \(belong_x\)：表示 \(x\) 这个元素属于哪个分块。
• \(lazy_x\)：懒标记，同线段树。
• \(L_x\) 和 \(R_x\)：划定第 \(x\) 个块的区间范围。

仅此而已。

---

ST 表

引入

ST 表是解决 可重复贡献问题 的数据结构。

什么是可重复贡献问题呢？举个例子，区间最大值，\(\max[1,5]\) 就是 \(\max(\max[1,4],\max[3,5])\) ，虽然 \([3,4]\) 重合了，但并不影响结果，这就是 可重复贡献。相反，区间和就不是可重复贡献问题，同一个部分不能多次被计算。

可重复贡献问题还要满足结合律，也就是说运算 \(\operatorname{opt}\) 的查询是可重复贡献问题，就必须满足：

\[(x\operatorname{opt} y) \operatorname{opt} z = x\operatorname{opt} (y \operatorname{opt} z) \]

RMQ 问题，即区间最大（小）值，和 \(\gcd\) 都是可重复贡献问题。

ST表运用了 倍增 的思想。通过 ST 表，我们可以实现 \(O(n \log n)\) 预处理，\(O(1)\) 查找。

简单来说，倍增思想就是把线性的处理转化为对数级的处理。

这里我们结合 【模板】ST 表，以最大值为例。

预处理

我们用 \(st(i,j)\) 代表区间 \([i,i+2^j-1]\) 的最大值。也就是说 \(st(i,1)\) 就是第 \(i\) 个数本身。我们先来思考递推式。
5,4,3,2,1——想出来了？揭晓答案：

\[st(i,j)=\max (st(i,j-1),st(i+2^{j-1},j-1)) \]

通过这个递推式完成 \(O(n \log n)\) 的预处理，接下来的查找就好办了。

代码如下：

void init()
{
	for(int j=1;j<=21;++j)//21属于是很极限了，这么写属于是省事，其实不需要到21的
		for(int i=1;i+(1<<j)-1<=n;++i)
			st[i][j]=max(st[i][j-1],st[i+(1<<(j-1))][j-1]);
}

查询

如何得到 \([i,j]\) 的最大值呢？我们说过，RMQ 是一个可重复贡献问题，所以查询的过程很简单：

1. 如果区间有 \(d\) 个元素，找到最接近 \(d\) 且小于 \(d\) 的 2 的整数次幂，其幂指数为 \(k\)。
2. 查询 \(\max(st(i,k),st(j-2^k,k))\)

代码如下：

int query(int l,int r)
{
	int bit=log2(r-l+1);
	return max(st[l][bit],st[r-(1<<bit)+1][bit]);
}

（又被 \(dalao\) 批了QAQ 不要二进制拆分求 \(\log\) ，复杂度++）

---

LCA 的倍增算法

LCA，即最近公共祖先。

预处理

LCA 的倍增算法也是倍增家族的一员，和 ST表 有异曲同工之妙，在用倍增解决最近公共祖先问题时我们用 \(fa(i,j)\) 表示点 \(i\) 的第 \(2^j\) 个祖先。所以，\(fa(i,0)\) 其实就是点 \(i\) 的父节点。

学习了 ST 表，LCA 的递推式应该同样问题不大。如下：

\[fa(i,j)=fa(fa(i,j-1),j-1) \]

代码则有一些小小的不同，因为是树，所以需要先遍历一波，确定初始状态 \(fa(i,0)\)。

（被 \(dalao\) 骂代码 shit 一样了 QAQ 放改进版）

void dfs(int x)
{
	for(int i=1;i<=20;++i)	f[x][i]=f[f[x][i-1]][i-1];
	for(auto i:e[x])
    		if(i!=f[x][0])
            		{f[i][0]=x;	dep[i]=dep[x]+1;	dfs(i);}
}

查询

你可能注意到了在搜索中我们记录了每个节点的深度，这也是很重要的一环。在查询两个点的 LCA 时，大致分为以下几个步骤：

1. 深度深的一点向上跳转至他的祖先节点，直至和另一点深度相同。
2. 深度相同后，两点是同一个节点，则该节点为两点的 LCA。
3. 深度相同后，两点仍不相同，则继续向上跳转至其祖先节点。
4. 如果两个节点的祖先节点相同，则不要跳转，这个祖先节点可能不是两点的 最近 公共祖先。当两个点的父节点相同时，该父节点是两点的 LCA。

文字说可能比较乏味？那我来个图：

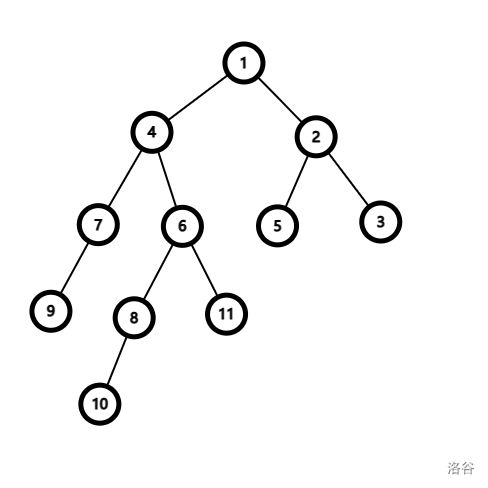
查询 \(10\) 和 \(2\) 的 LCA，操作步骤如下：

1. \(dep_{10}>dep_2\)，深度差 3。开始跳转：\(10 \to fa(10,1)=6 \to fa(6,0)=4\)。
2. 同深度，节点不同，继续跳转。两点父节点相同，父节点 \(1\) 就是 \(10\) 和 \(2\) 的 LCA。

大概来说就是这样了，下面是代码：

int LCA(int u,int v)
{
	if(dep[u]<dep[v])	swap(u,v);//个人习惯，每次都让u的深度更深
	int len=dep[u]-dep[v];
	for(int i=20;i>=0;--i)	if(len&(1<<i))	u=f[u][i];//深度差二进制拆分，跳转
	if(u==v)	return u;
	for(int i=20;i>=0;--i)	if(f[u][i]!=f[v][i])	u=f[u][i],v=f[v][i];//只有祖先节点不同才跳
	return f[u][0];
}

树上差分

这里顺便小提一嘴树上差分。顾名思义，和差分逻辑相同，只不过用在了树上。

如果想给路径 \(u \to v\) 的所有节点都加上 \(k\) ，树上差分时，就进行如下操作：

\[diff_u \gets diff_u+1 \]

\[diff_v \gets diff_v+1 \]

\[diff_{\operatorname{lca}(u,v)} \gets diff_{\operatorname{lca}(u,v)}-1 \]

\[diff_{fa(\operatorname{lca}(u,v))} \gets diff_{fa(\operatorname{lca}(u,v))}-1 \]

代码如下：

void make_diff()
{
	for(int i=1;i<n;++i)
	{
		int LCA=lca(a[i],a[i+1]);
		diff[fa[a[i]][0]]++;
		diff[a[i+1]]++;
		diff[LCA]--;
		diff[fa[LCA][0]]--;
	}
}

(结合上面 LCA 的代码哦)

计算最终结果的方法有很多，可以用 dfs 序的逆序，也可以先拓扑排序。

看到这，你就可以试试做一下 P3258 [JLOI2014]松鼠的新家 了，它相当于 LCA 和树上差分的模板题。

---

树链剖分

引入

我们这里说的树链剖分指的是 重链剖分。首先，我们先来介绍几个简单的概念。

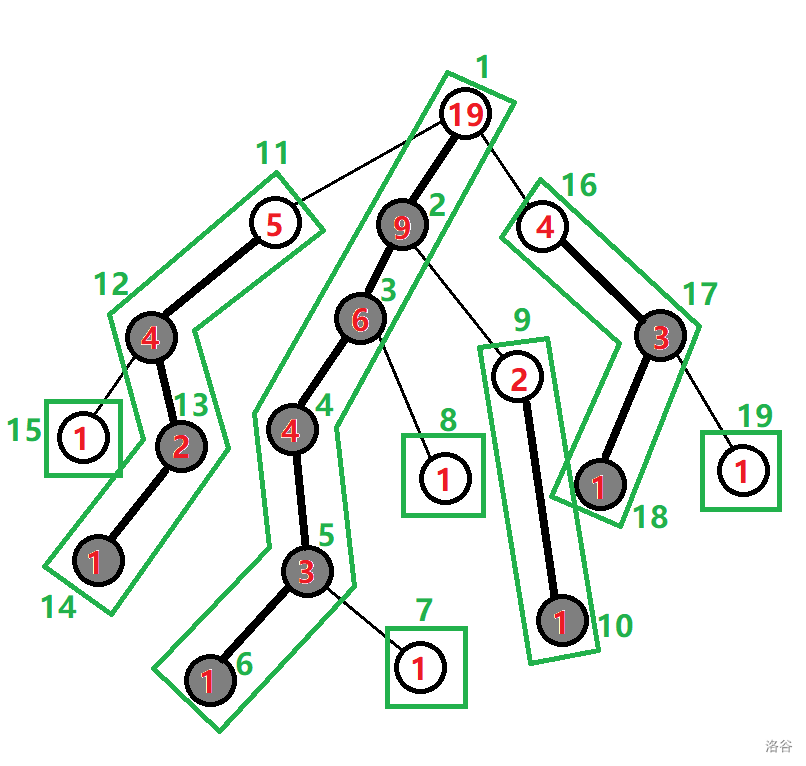
从 OI - WIKI 借了半张图。（之所以是半张图是因为 TSOI 的树剖做法和大众做法略有不同）我们开始介绍：

• 重儿子：一个节点子节点中子树最大的子节点。图中的灰色节点都是重儿子。
• 轻儿子：与重儿子对应，除了重儿子之外的所有子节点都是轻儿子。
• 重边：从当前节点到其重儿子的边。图中的加粗边都是重边。
• 轻边：从当前节点到其轻儿子的边。
• 重链：由若干条重链首尾衔接构成的路径。
• 链深度：这便是 TSOI 与大众做法不同的地方——在树剖中，我们记录的节点深度 \(dep_u\) 表示从 \(u\) 到根节点的路径经过了几条重链。（落单的节点也算做一条重链）

接下来我们要引入一个老朋友，并让他发挥新的作用。

DFS 序

其实就是 tarjan 算法
中的时间戳啦~

DFS 序有一个特点，就是 一棵子树的所有节点 的DFS 序是 相邻的。比如这棵树：

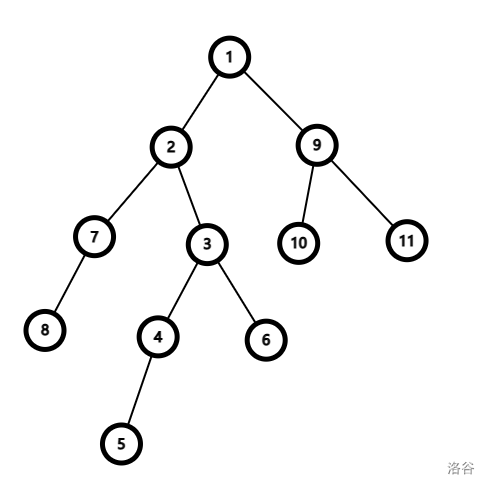
用 DFS 序排完后，子树 \(subtree_4\) 的所有节点的 DFS 序正好是 \([4,8]\)。（子树的区间左边界就是这棵子树根节点的 DFS 序，收集子树的区间右边界可以在 DFS 时进行）

如果在 DFS 时优先遍历重儿子，那么 一条重链上的所有节点 的DFS 序也是 相邻的。比如重链 \(1 \to 2 \to 3 \to 4 \to 5\)。

由此一来，我们就可以对一棵树进行 重链剖分 ，然后对 DFS 序建立 线段树，把 路径/子树改变和查询问题 转换成若干个 区间改变和区间查询问题 了。

化树为线

一般来说，树上操作分为两类：

• 子树操作：直接对子树的 DFS 序区间进行操作即可。
• 路径操作：需要拆成多个区间。

如何将路径转换为区间？方法类似于 LCA，我们用\(fa_u\) 代表 \(u\) 的父节点；用 \(root_u\) 代表 \(u\) 所在重链的最小 DFS 序节点，如上图中:

\[root_5=root_4=root_3=root_2=root_1=1 \]

下文全部用 DFS 序描述节点，码代码时注意标号和 DFS 序的切换。

接下来，对于路径 \(u \to v\)，我们拆成如下几个区间：

1. 链深度不同：深度更深的节点 \(u\) 跳转至 \(fa_{root_u}\)，\([root_u,u]\) 是需要进行操作的区间；
2. 链深度相同且 \(root_u \not= root_v\)：\(u\) 跳转至 \(fa_{root_u}\)，\(v\) 跳转至 \(fa_{root_v}\)，\([root_u,u]\) 和 \([root_v,v]\) 是需要进行操作的区间；
3. 链深度相同且 \(root_u = root_v\)：\([u,v]\) 是需要进行操作的区间之一（\(u<v\)） ，结束。

说起来也不是那么难？
三道题送给大家：P4092 [HEOI2016/TJOI2016]树、【模板】重链剖分/树链剖分、P2486 [SDOI2011]染色。
这里是后两道题的 \(AC\) \(CODE\)，祝你好运……

讲讲 染色

关于 P2486 [SDOI2011]染色，可以给你一些提示，我好不容易总结出的 “ 王氏染色定则 ” ：

在染色 这道题中，路径修改具有如下三个特性：

1. 层次性：对一条有根树重链剖分，链深度 高 的点的 DFS 序一定比链深度 低 的点大
2. 对称单调性：两点的路径经过的所有节点的 DFS 序组成的 有序序列 从两点的 最近公共祖先 向两边 严格递增。
3. 方向性：该序列从 最近公共祖先 拆分为 两段 后，每一段即为最近公共祖先到这两点中一点的 路径。

举个例子：

1. \(11\) 的 DFS 序比 \(8\) 大（\(dep_8=2,dep_{11}=3\)）
2. 这条路径组成的有序序列是：\([8,7][2,1][9,9][11,11]\)（一个区间代表跨过了一条链），这个序列从 \(\operatorname{lca}(8,11)=1\) 向两边严格递增。
3. 从 \(1\) 处拆开，\([1,2][7,8]\) 和 \([1,1][9,9][11,11]\) 就是 \(1 \to 8\) 和 \(1 \to 11\) 的路径。

希望可以给你写路径查询的代码一些启发。

有问题随时补充，目前就是这样。

标签：标记,int,线段,DFS,关于,区间,数据结构,节点
From： https://www.cnblogs.com/michaelwong007/p/data-structure.html